
- •1. Производная. Правила дифференцирования
- •2. Таблица производных
- •3. Правила дифференцирования
- •4. Производные высших порядков
- •5. Дифференцирование функций, заданных неявно или параметрически
- •6. Уравнения касательной и нормали
- •7. Дифференциал первого порядка
- •8. Дифференциалы высших порядков. Формула Тейлора
- •9. Раскрытие неопределённостей по правилу Лопиталя
- •Задание 1
- •Задание 8
- •Задание 13
- •Задание 14
- •Задание 15
- •Задание 16
- •Задание 17
- •394026 Воронеж, Московский просп., 14
Задание 8
Проверьте, что данная функция удовлетворяет дифференциальному уравнению.
1)
![]() ,
, ![]() ;
;
2)
![]() ,
, ![]() ;
;
3)
![]() ,
, ![]() ;
;
4)
![]() ,
, ![]() ;
;
5)
![]() ,
, ![]() ;
;
6)
![]() ,
, ![]() ;
;
7)
![]() ,
, ![]() ;
;
8)
![]() ,
, ![]() ;
;
9)
![]() ,
, ![]() ;
;
10)
![]() ,
, ![]() ;
;
11)
![]() ,
, ![]() ;
;
12)
![]() ,
, ![]() ;
;
13)
![]() ,
, ![]() ;
;
14)
![]() ,
, ![]() ;
;
15)
![]() ,
, ![]() ;
;
16)
![]() ,
, ![]() ;
;
17)
![]() ,
, ![]() ;
;
18)
![]() ,
, ![]() ;
;
19)
![]() ,
, ![]() ;
;
20)
![]() ,
, ![]() ;
;
21)
![]() ,
, ![]() ;
;
22)
![]() ,
, ![]() ;
;
23)
![]() ,
, ![]() ;
;
24)
![]() ,
, ![]() ;
;
25)
![]() ,
, ![]() ;
;
26)
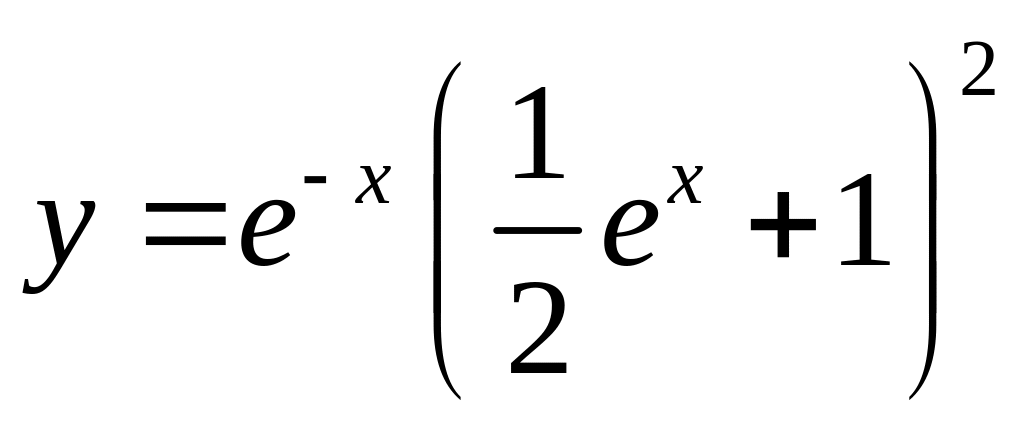 ,
, ![]() ;
;
27)
![]() ,
, ![]() ;
;
28)
![]() ,
, ![]() ;
;
29)
![]() ,
, ![]() ;
;
30)
![]() ,
, ![]() .
.
Задание 9
Найдите
,
![]() .
.
1)
![]() ; 2)
; 2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
;
10)
![]() ; 11)
; 11)
![]() ;
12)
;
12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
15)
;
15)
![]() ;
;
16)
![]() ;
17)
;
17)
![]() ;
18)
;
18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ; 21)
; 21)
![]() ;
;
22)
![]() ; 23)
; 23)
![]() ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
![]() ;
27)
;
27)
![]() ;
;
28)
![]() ;
29)
;
29)
![]() ;
30)
;
30)
![]() .
.
Задание 10
Найдите производную n-го порядка.
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
;
15)
![]() ; 16)
; 16)
![]() ;
;
17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ;
;
21)
![]() ; 22)
; 22)
![]() ;
;
23)
![]() ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
![]() ;
;
27)
![]() ; 28)
; 28)
![]() ;
;
29)
![]() ; 30)
; 30)
![]() .
.
Задание 11
Найдите производную указанного порядка.
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ; 10)
; 10)
![]() ;
;
11)
![]() ; 12)
; 12)
![]() ;
;
13)
![]() ; 14)
; 14)
![]() ;
;
15)
![]() 16)
16)
![]() ;
;
17)
![]() ; 18)
; 18)
![]() ;
;
19)
![]() ; 20)
; 20)
![]() ;
;
21)
![]() ; 22)
; 22)
![]() ;
;
23)
![]() ; 24)
; 24)
![]() ;
;
25)
![]() ; 26)
; 26)
![]() ;
;
27)
![]() ;28)
;28)
![]() ;
;
29)
![]() ;
30)
;
30)
![]() .
.
Задание 12
Найдите производные первого и второго порядков в точке M(x0, y0) от функции, заданной неявно.
1)
![]() ,
M(1;
1) ; 2)
,
M(1;
1) ; 2)
![]() ,
M(1;
-/4)
;
,
M(1;
-/4)
;
3)
![]() ,
M(1;
-1) ; 4)
,
M(1;
-1) ; 4)
![]() ,
M(0;
/4)
;
,
M(0;
/4)
;
5)
![]() ,
M(1;
1) ; 6)
,
M(1;
1) ; 6)
![]() ,
M(0;
/4)
;
,
M(0;
/4)
;
7)
![]() ,
M(0;
1) ; 8)
,
M(0;
1) ; 8)
![]() ,
M(1;
0) ;
,
M(1;
0) ;
9)
![]() ,
M(0;
1) ; 10)
,
M(0;
1) ; 10)
![]() ,
M(1;
1) ;
,
M(1;
1) ;
11)
![]() ,
M(2;
-1); 12)
,
M(2;
-1); 12)
![]() ,
M(0;
2) ;
,
M(0;
2) ;
13)
![]() ,
M(1;
1) ; 14)
,
M(1;
1) ; 14)
![]() ,
M(2;
1) ;
,
M(2;
1) ;
15)
![]() ,
M(4/;
/4)
; 16)
,
M(4/;
/4)
; 16)
![]() ,
M(1;
2) ;
,
M(1;
2) ;
17)
![]() ,
M(-1;
0) ; 18)
,
M(-1;
0) ; 18)
![]() ,
M(0;
1) ;
,
M(0;
1) ;
19)
![]() ,
M(0;
/2);
20)
,
M(0;
/2);
20)
![]() ,
M(0;
/2)
;
,
M(0;
/2)
;
21)
![]() ,
M(0;0)
22)
,
M(0;0)
22)
![]() ,
M(3;
0);
,
M(3;
0);
23)
![]() ,
M(1/4;1)
;
,
M(1/4;1)
;
24)
![]() ,
M(1;0)
;
,
M(1;0)
;
25)
![]() ,
M(0;0)
; 26)
,
M(0;0)
; 26)
![]() ,
M(0;1)
;
,
M(0;1)
;
27)
![]() ,
M(0;0);
,
M(0;0);
28)
![]() ,
M(0;0)
;
,
M(0;0)
;
29)
![]() ,
M(0;1)
; 30)
,
M(0;1)
; 30)
![]() ,
M(0;1).
,
M(0;1).
Задание 13
Найдите производные 1-го и 2-го порядков от функций, заданных параметрически.
1)
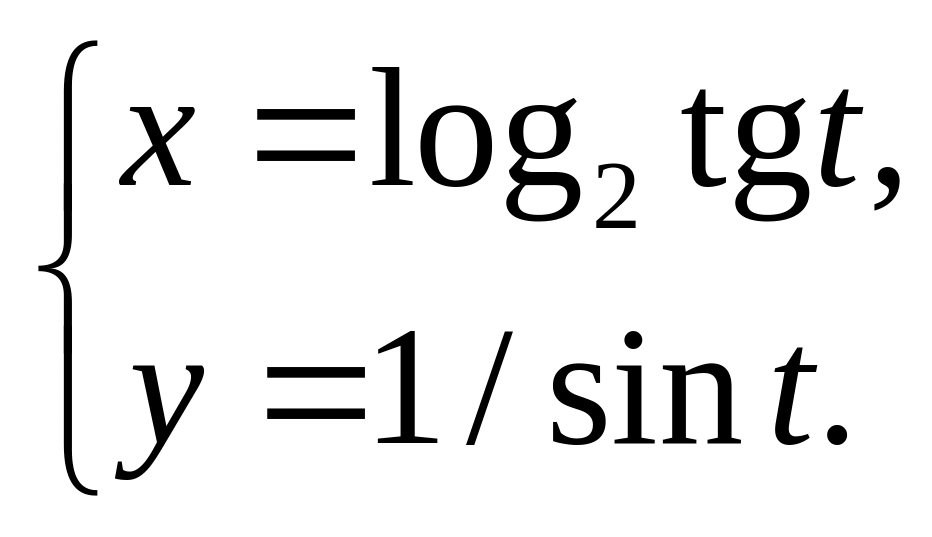 2)
2)
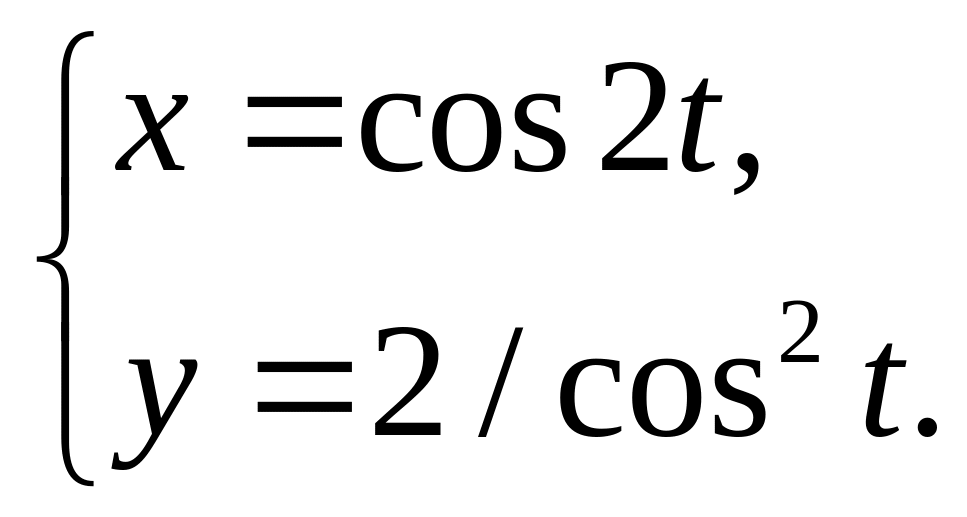
3)
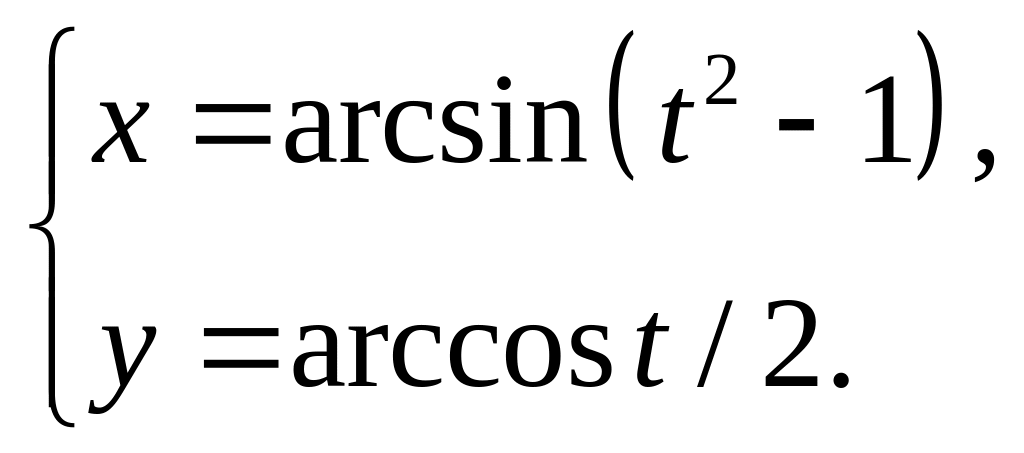 4)
4)
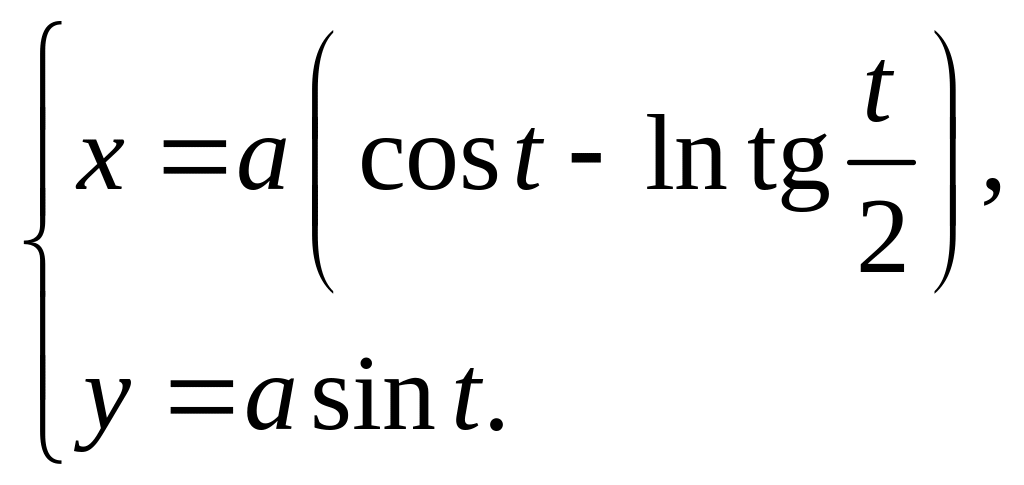
5)
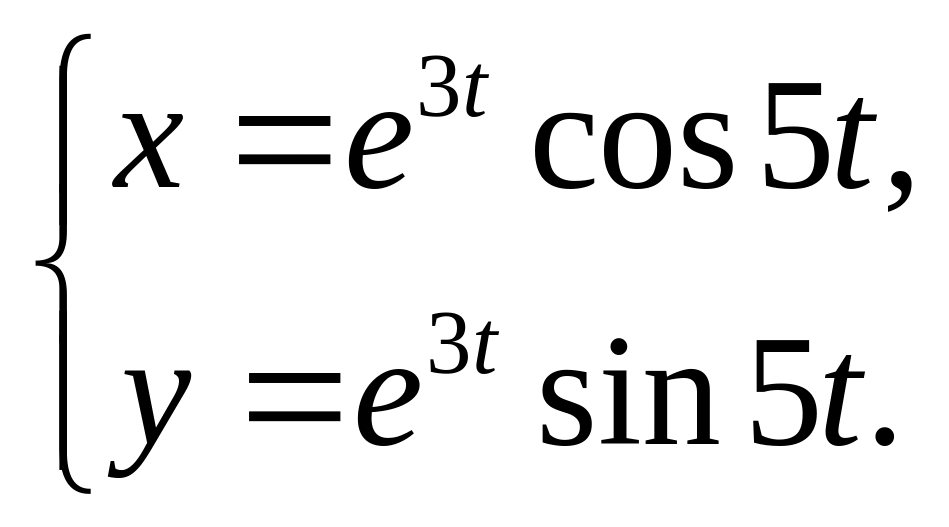 6)
6)
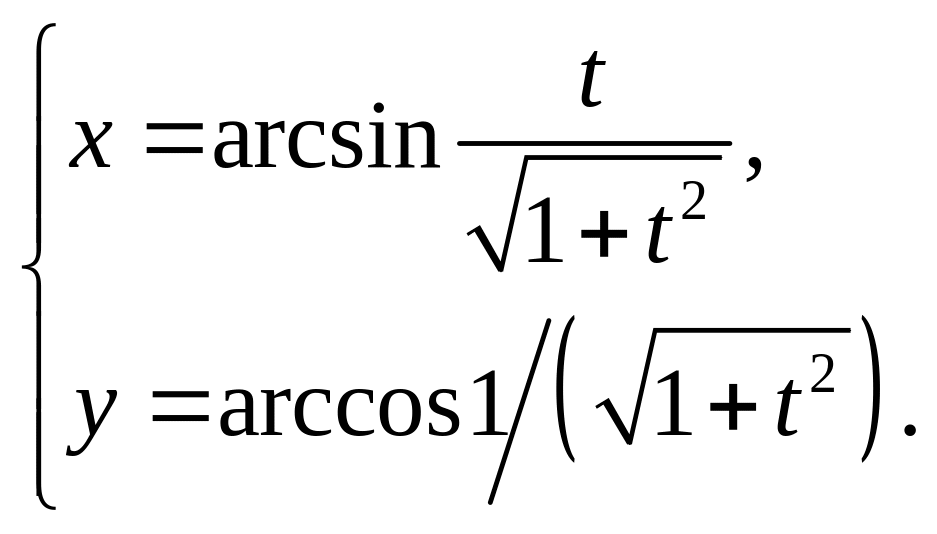
7)
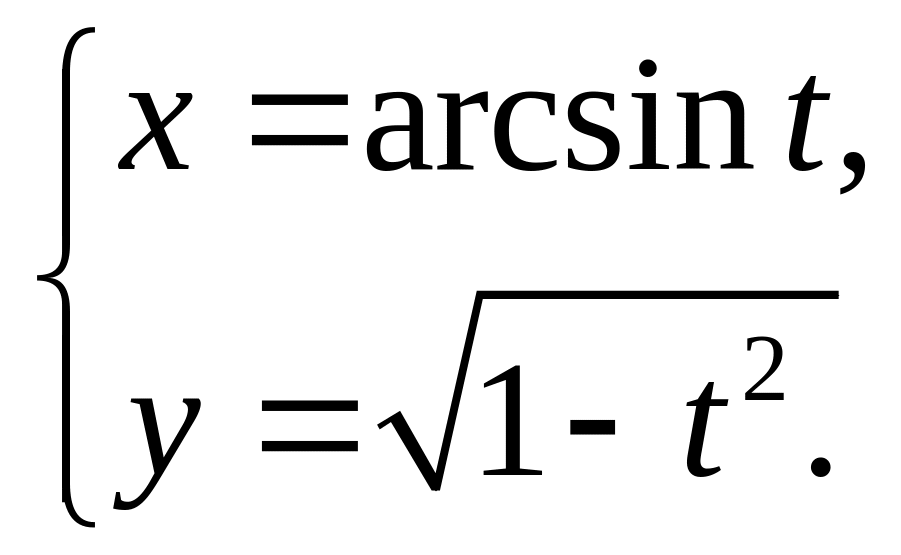 8)
8)

9)
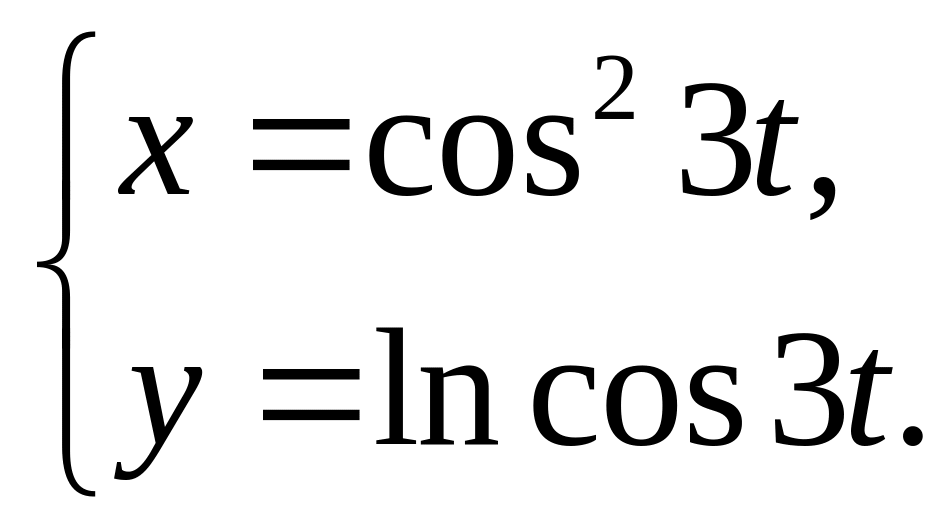 10)
10)
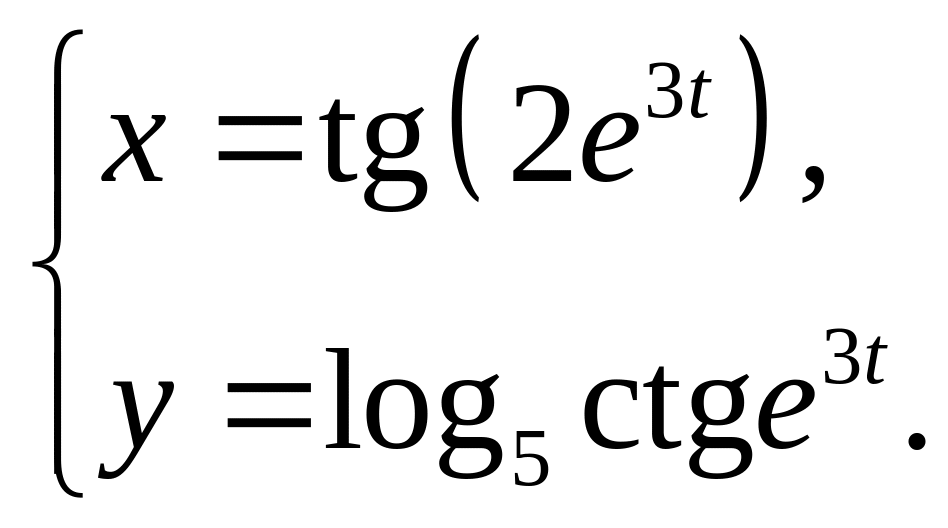
11)
![]() 12)
12)
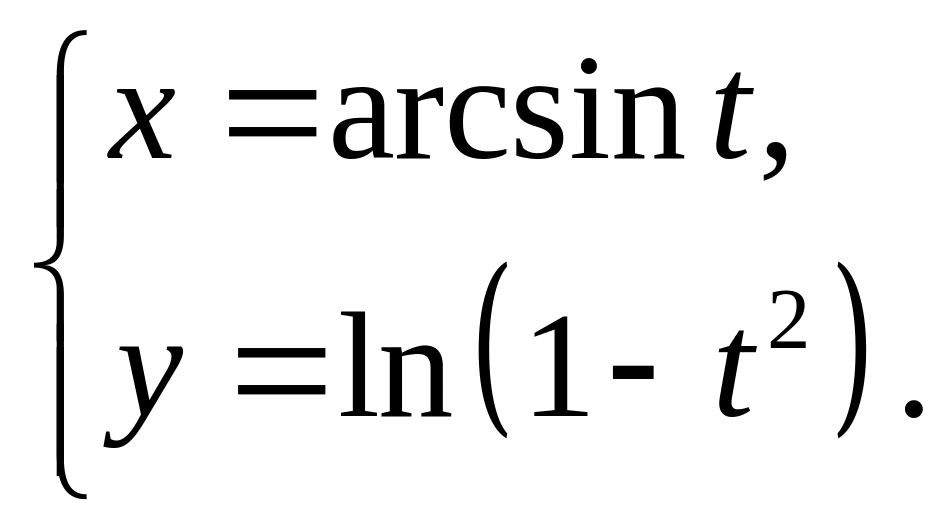
13)
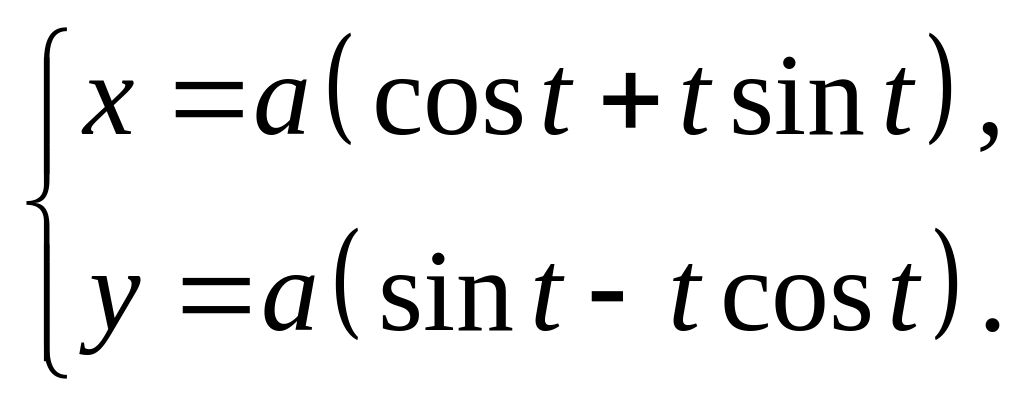 14)
14)

15)
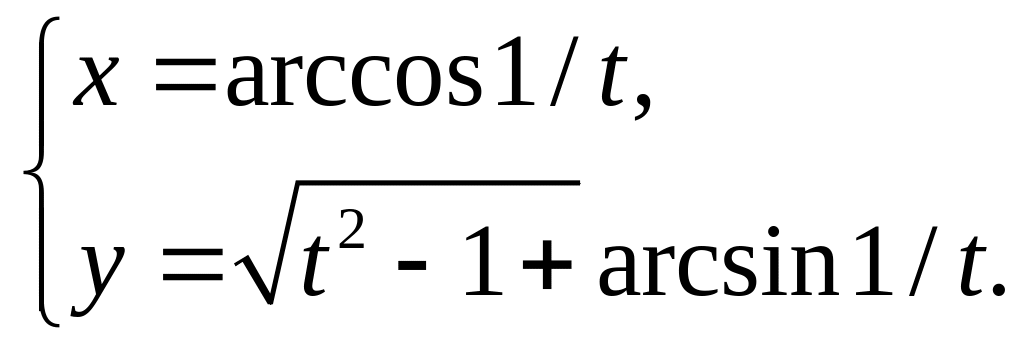 16)
16)
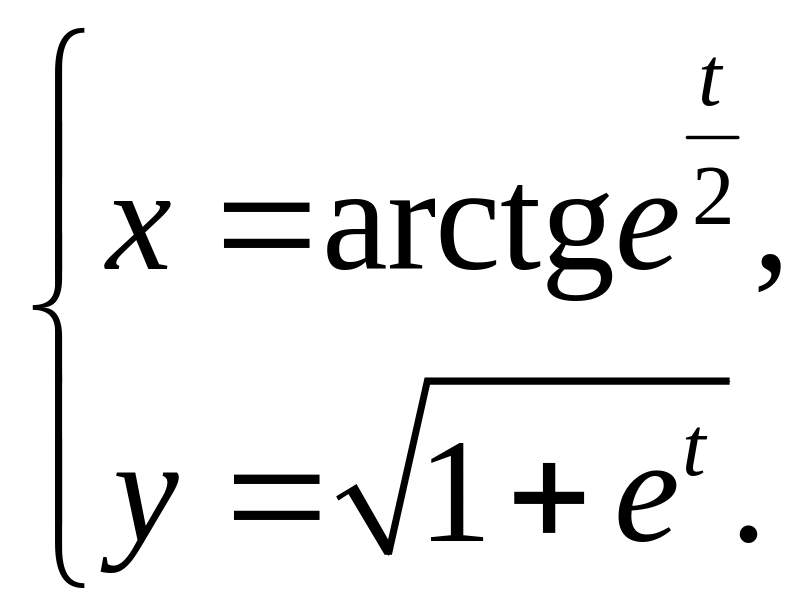
17)
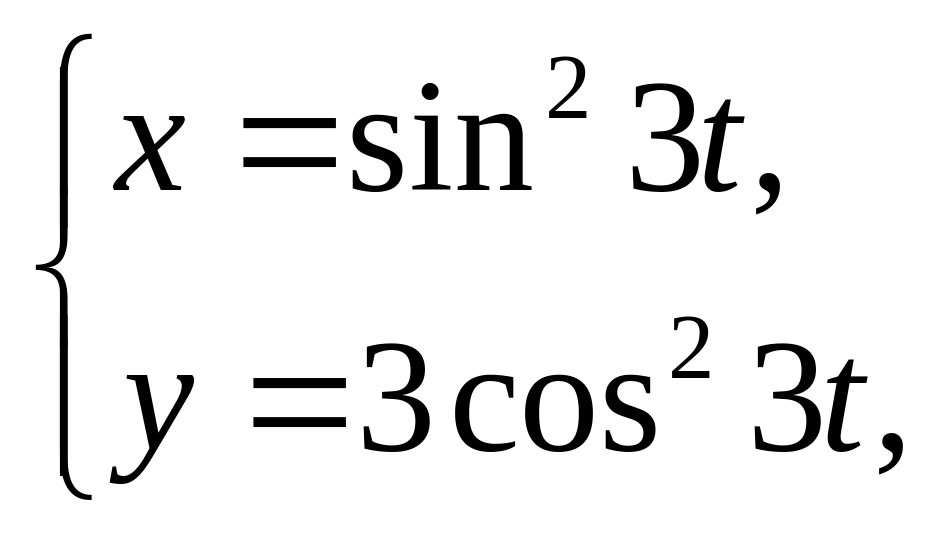 18)
18)
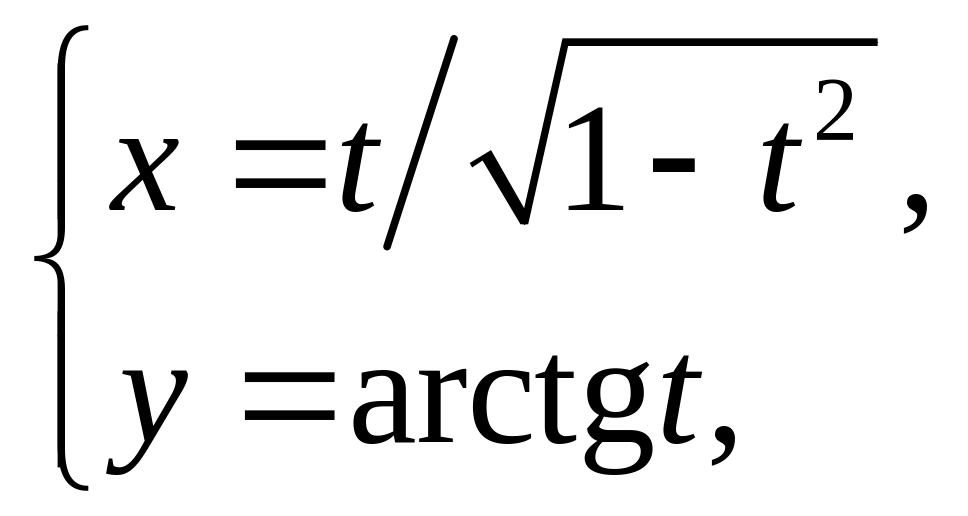
19)
![]() 20)
20)
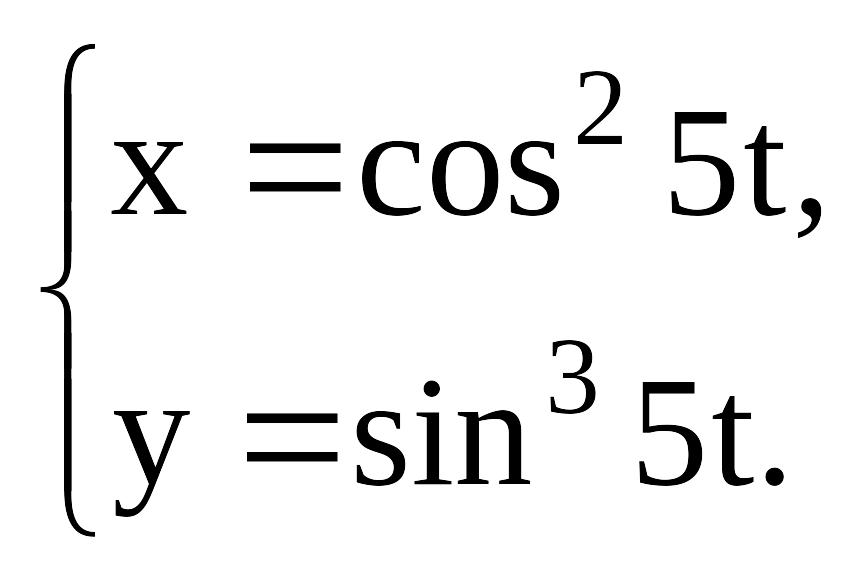
21)
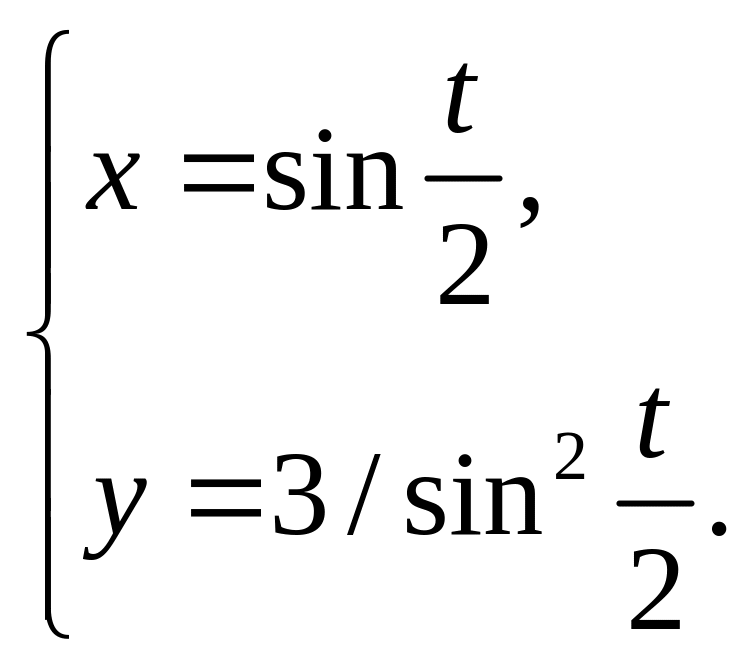 22)
22)
![]()
23)
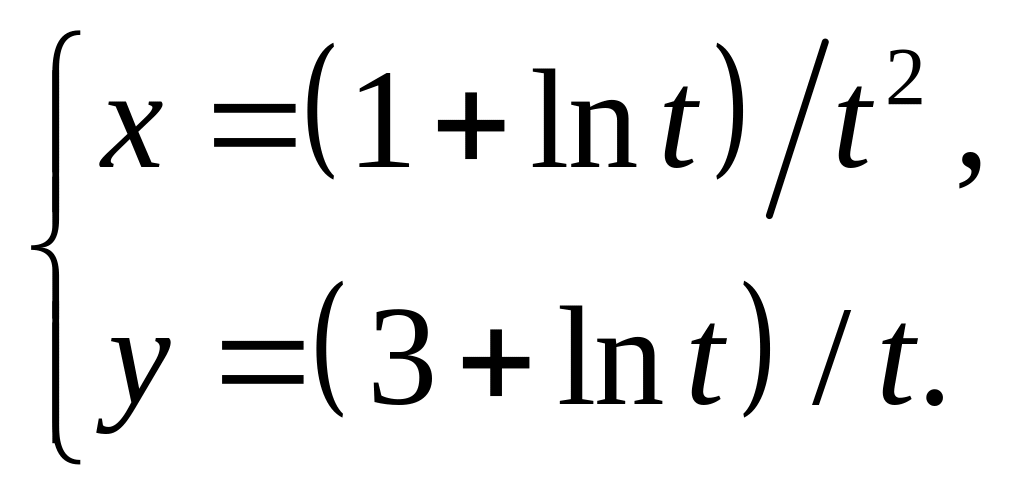 24)
24)
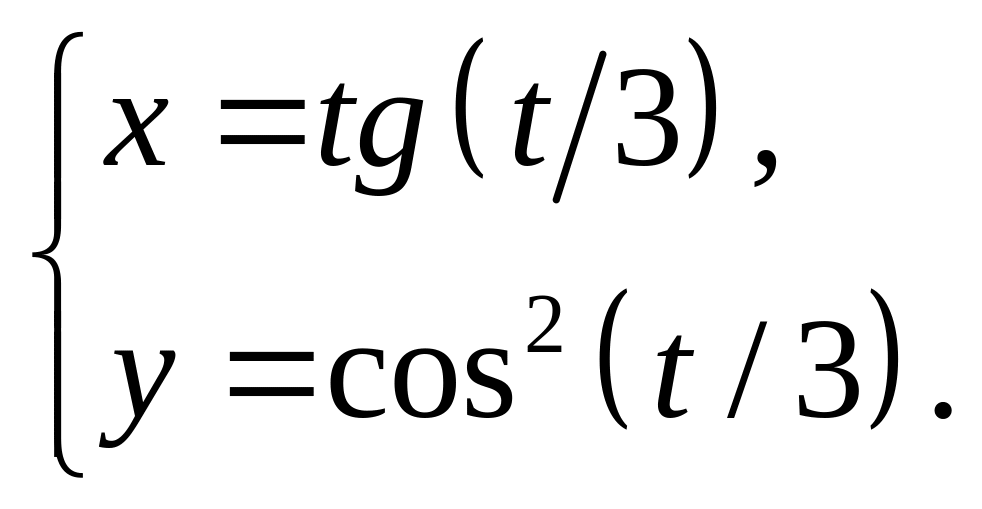
25)
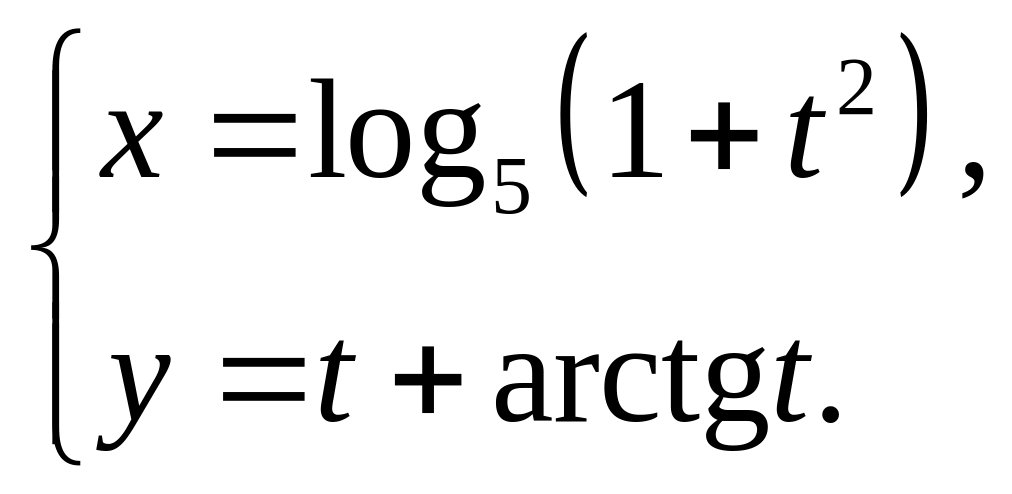 26)
26)
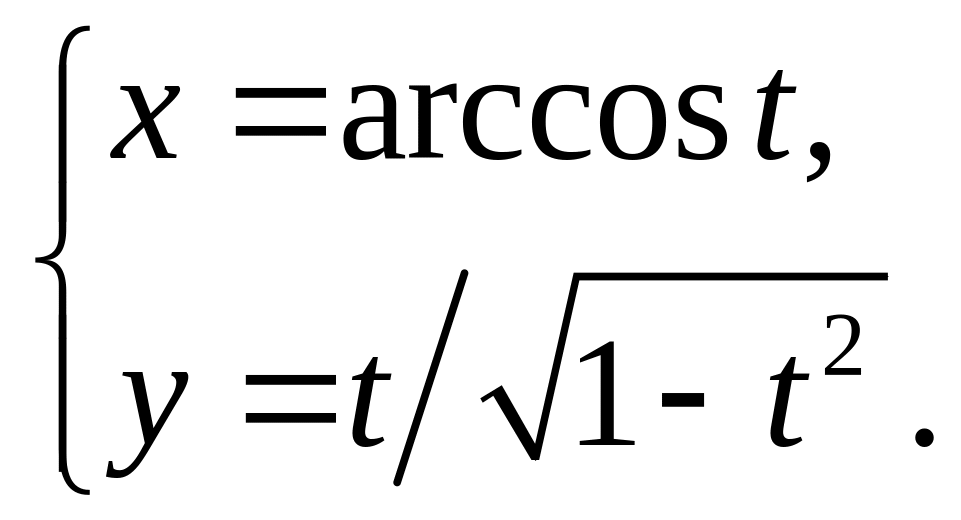
27)
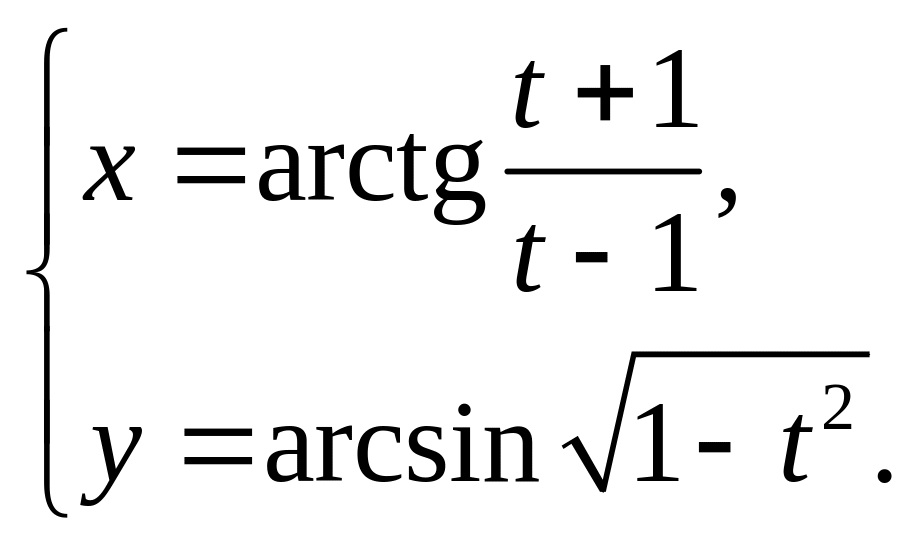 28)
28)
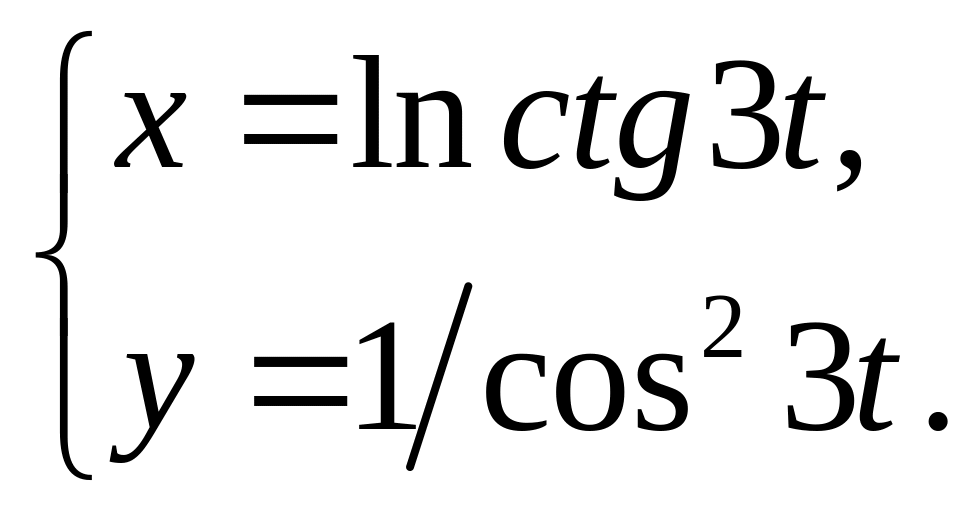
29)
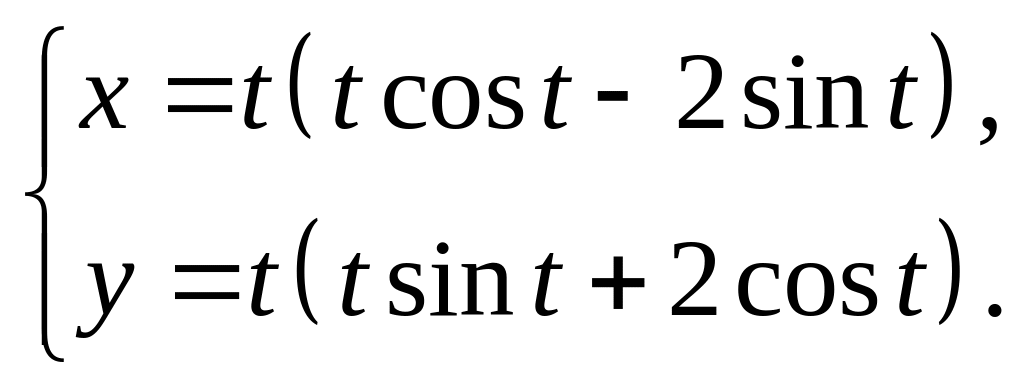 30)
30)
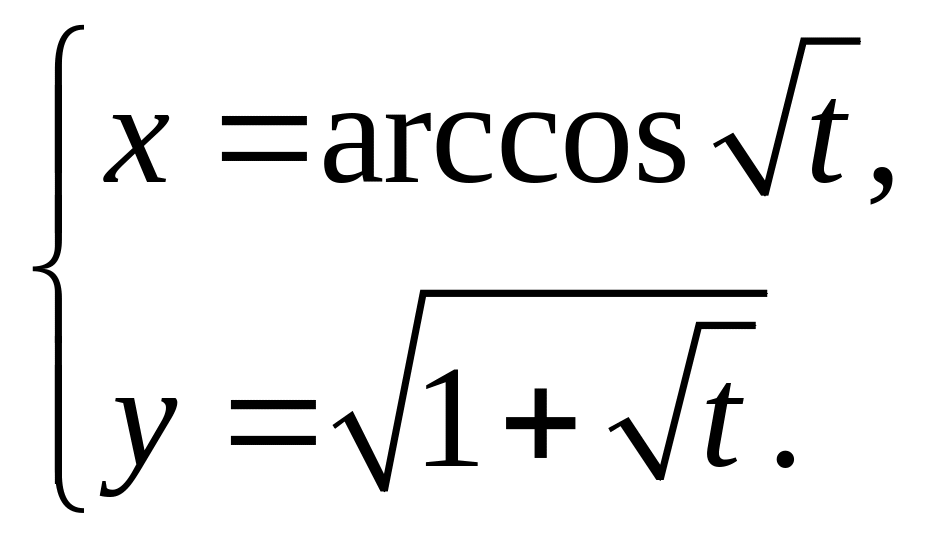
Задание 14
Используя дифференциал первого порядка, найдите приближённо (ln2 0,693, ln3 1,099, ln5 1,609, 3,1416).
1)
![]() ;
2)
;
2)
![]() ;
3) arctg 1,05; 4)
;
3) arctg 1,05; 4)
![]() ;
;
5)
arcsin 0,05; 6)
![]() ;
7) 32,1;
8)
;
7) 32,1;
8)
![]() ;
9) arctg 0,9; 10)
;
9) arctg 0,9; 10)
![]() ;
11) cos 1; 12) 51,9;
;
11) cos 1; 12) 51,9;
13)
![]() ;
14)
;
14)
![]() ;
15) tg 1; 16) 41,8;
;
15) tg 1; 16) 41,8;
17)
![]() ;
18) sin 320;
19)
;
18) sin 320;
19)
![]() ;
20) tg 440;
;
20) tg 440;
21)
23,1;
22) cos 310;
23)
![]() ;
24) 31,8;
;
24) 31,8;
25) ctg 470; 26) arctg 1,2; 27) sin 880; 28) 23,8;
29)
cos 930;
30)
![]() .
.
