2.1.5. Содержание отчета и его форма

Отчет должен содержать схему, описание лабораторного испытательного стенда и основные расчетные зависимости. Результаты замеров и вычислений вносятся в отчет в виде табл.2.

Таблица 2

Результаты замеров и вычислений

	Сжатый воздух					Разреженный воздух
Жидкость	Левое колено	Правое колено	см	Па	Па	Левое колено	Правое колено	см	Па	Па
1	2	3	4	5	6	7	8	9	10	11
Вода
Спирт

мм. рт. ст.; Па = .

2.2. Лабораторная работа: относительный

ПОКОЙ ЖИДКОСТИ

ЦЕЛЬ РАБОТЫ – экспериментальное установление формы свободной поверхности жидкости в круглом цилиндрическом сосуде, вращающемся с постоянной угловой скоростью вокруг собственной вертикальной оси, и аппроксимация (приближение) формы свободной поверхности, полученной из опыта, теоретическим параболоидом вращения.

СОДЕРЖАНИЕ РАБОТЫ – изучение поведения тяжелой капельной жидкости, находящейся во вращающемся сосуде, с сопоставлением расчетных и экспериментальных результатов.

2.2.1. Теоретические основы.

Состояние, когда жидкость в покое относительно стенок сосудов, вращающихся с ускорением, называют обычно относительным покоем. В соответствии с известным принципом механики при пользовании уравнениями равновесия в ситеме координат, которая движется с ускорением, мы должны в число действующих массовых сил включить также силы инерции переносного движения, направленные в сторону, противоположную направлению движения.

Пусть открытый вертикальный прямой круглый цилиндрический сосуд с жидкостью вращается вокруг своей оси с постоянной угловой скоростью . Жидкость, постепенно увлекаясь во вращение вследствие вязкости, в установленном режиме вращается вместе с сосудом, как единое целое с той же угловой скоростью , т.е. находится в состоянии покоя относительно стенок сосуда. Это состояние поддерживается равновесием сил гидростатического давления (Р), тяжести (g) и центробежной силы инерции ( ), действующих на каждую частицу жидкости (сила вязкого трения в установившемся состоянии относительного покоя отсутствует). Из уравнения равновесия Эйлера получается следующее распределение давлений в жидкости:

, ( 2.3 )

где z – ордината жидкой частицы, отсчитанная по вертикали вверх от самой нижней точки свободной поверхности;

r – расстояние до частицы по горизонтали от оси вращения;

 - угловая скорость вращения;  - плотность жидкости;

g – ускорение силы тяжести (g = 9,81 );

Р – давление в жидкой частице с координатами z и r.

Из выражения (2.3) при Р = const (dP = 0) получаются уравнения поверхностей равного давления, образующих семейство осесимметричных параболоидов вращения с общей осью z. В частности, при получается уравнение свободной поверхности, любое меридиональное сечение которой представляет собой параболу с вертикальной осью симметрии:

. ( 2.4 )

Как видно из последнего уравнения, форма свободной поверхности определяется только параметрами и r и не зависит от рода используемой жидкости.

2.2.2. Математическая обработка наблюдений.

Вычисляются расстояния от оси вращения до симметрично расположенных левых и правых точек с номером i по формуле:

.

Опытные значения координат наносятся на график симметрично относительно оси z и соединяются ломаной кривой (рис.9).

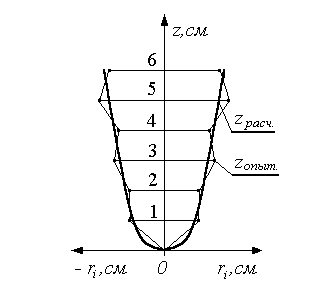
Рис.9. Согласование опытных и расчетных данных

Форма этой кривой напоминает параболу, поэтому опытную кривую аппроксимируют уравнением:

. ( 2.5 )

Из уравнения (2.5) для неизвестного коэффициента А получается соотношение:

. ( 2.6 )

Подставляя в уравнение (2.6) вместо r и z их опытные значения (i = 1, 2…N, где N – число наблюдений), вычисляют опытные значения коэффициента по формуле:

, ( i = 1, 2…N)

и заносят их в табл.3. Легко видеть, что в разных наблюдениях значения отличаются друг от друга. В качестве оценки истинного значения коэффициента А принимают среднее арифметическое:

. ( 2.7 )

Используя найденную величину коэффициента по уравнению (2.7) и придавая r значения (i = 1, 2,…N), вычисляем по формуле (2.5) и заносим в табл.3 теоретические значения. Точки ( ) наносим на график (см. рис.9) и соединяем их плавной кривой. Это и есть наблюдаемая форма свободной поверхности жидкости в сосуде, вращающемся с постоянной угловой скоростью.

Для определения угловой скорости  из уравнений (2.4) и (2.7) получаем соотношение:

. ( 2.8 )

Найденную угловую скорость  пересчитываем в число оборотов в минуту по формуле :

. ( 2.9 )

Следует сравнить рассчитанное число оборотов с опытным , отмеченным на приборе (или замеренным механическим тахометром) и объяснить расхождение.

2.2.3. Методика выполнения эксперимента.

Лабораторная установка (рис.10) состоит из открытого круглого цилиндрического сосуда 1, днище которого закреплено на вертикальном валу 2, расположенном на оси симметрии z сосуда. Сосуд, наполненный примерно на половину водой, приводится во вращение с постоянным числом n оборотов в минуту электродвигателем 3 через передачу 4. Определение координат свободной поверхности 5 производится с помощью координатника 6, закрепленного на неподвижной раме 7 прибора. По горизонтальным направляющим с миллиметровой шкалой 8 с помощью винта 9 перемещается каретка с измерительной иглой 10. Игла может перемещаться по вертикальным направляющим с миллиметровой шкалой 11 и фиксироваться винтом 12. Для отсчета горизонтальных и вертикальных координат на каретке и игле нанесены риски.

Рис.10. Схема лабораторной установки

2.2.4. Порядок выполнения работы на экспериментальной установке.

1. Отметить указанное на приборе число об./мин сосуда.

2. Включить электродвигатель 3 и дождаться установления состояния относительного покоя жидкости во вращающемся сосуде 1 (параболоид не меняет форму через 5-6 мин).

3. Установить измерительную иглу по оси параболоида, ввести острие в соприкосновение с поверхностью жидкости (в нижней точке параболоида) и произвести отсчеты по горизонтальной ( ) и вертикальной ( ) шкалам (нулевая точка).

4. Поднять иглу вверх на 1 см. Движением каретки влево с помощью винта 9 ввести остие иглы в соприкосновение с поверхностью жидкости. Произвести отсчет по горизонтальной шкале (первая левая точка).

5. Повторяя пункт 4, отсчитывают по горизонтальной шкале значения (i = 2, 3,…) для второй, третьей и последующих левых точек. Всего надо отметить 5-6 точек.

6. Оставив иглу, закрепленную винтом 12, на высоте, соответствующей последнему левому измерению, переместить каретку вправо до соприкосновения острия иглы с поверхностью жидкости справа от оси вращения, произвести отсчет по горизонтальной шкале (последняя правая точка; N – номер последней точки).

7. Повторить пункты 4 и 5 с тем лишь изменением, что теперь надо опускать иглу с шагом 1 см и производить горизонтальные правые отсчеты , и т.д. Возвращение иглы в нулевую точку ( ) свидетельствует о правильности измерений. В противном случае следует повторить измерения. Результаты измерений ( ) и расчетов по формулам раздела 2.2.2 занести в табл.3.

2.2.5. Порядок выполнения лабораторной работы на ПЭВМ.

1. Выполнить работы по п.п. 1-5 раздела 1.1.4.

2. Нажатием клавиши Tab переместить курсор в меню файлов Q BASIC и при помощи клавиши ↓ установить его на разделе Л.р. 10. bas.

3. Нажимая клавишу ENTER войти в файл программы Л.р. 10. bas.

4. Для запуска программы Л.р. 10. bas одновременно нажмите клавиши Shift и F5. На экране монитора откроется окно, содержащее информацию в соответствии с рис.11.

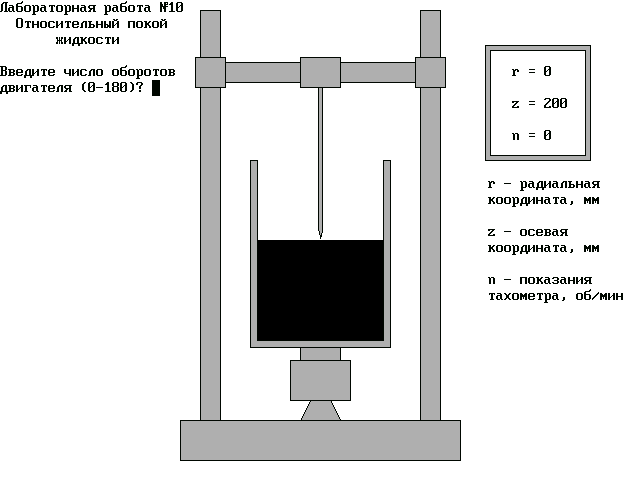
Рис.11. Содержание первого окна программы Л.р. 10.bas.

5. За знаком ? на месте мигающего курсора в соответствии со списком (см. рис.11) введите с клавиатуры необходимое число оборотов открытого цилиндрического сосуда, заполненного водой.

6. После нажатия клавиши ENTER откроется окно (рис.12), в котором можно наблюдать динамику протекания процесса и изменения формы свободной поверхности жидкости в зависимости от числа оборотов цилиндрического сосуда. В этом же окне приводится инструкция по пространственному перемещению конца измерительной иглы. При перемещении измерительной иглы ее координаты автоматически регистрируются и высвечиваются в информационном измерительном окне.

7. Руководствуясь инструкцией, помещенной в п. 6 и на рис.12, выполнить действия по п.п. 3-7 раздела 2.2.4.

8. По окончании выполнения исследований нажатием клавиш Е и ENTER остановить выполнение программы.

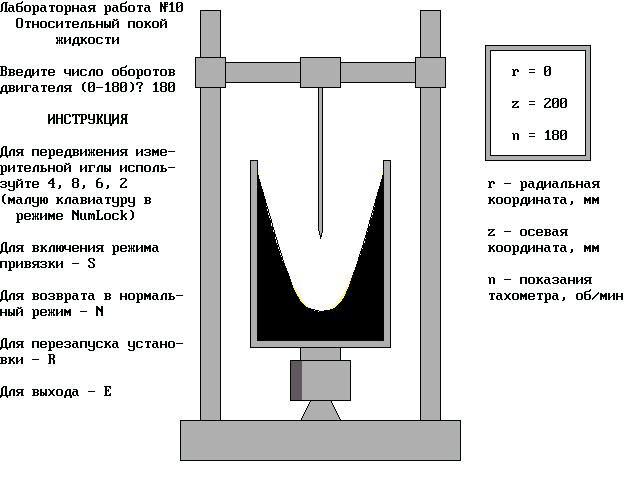
Рис.12. Содержание второго окна программы Л.р. 10.bas

9. Нажимая последовательно клавиши Alt и ← переместить курсор в меню программы Q BASIC к разделу «Файл» и, посредством клавиш ENTER и ↓ , подвести его в образовавшемся окне к разделу “Выход”.

10. Нажать клавишу ENTER и завершить работу программы Q BASIC.

11. Отключить системный блок и монитор компьютера от электросети.