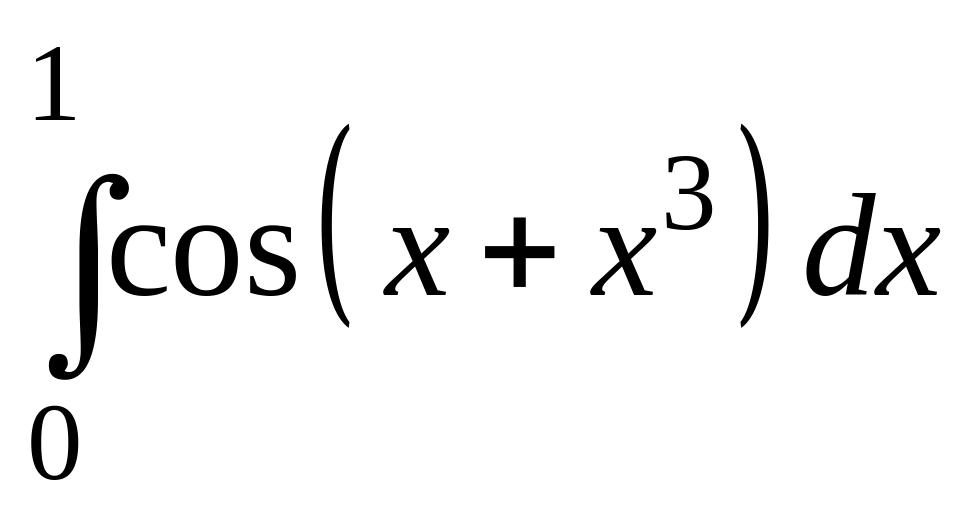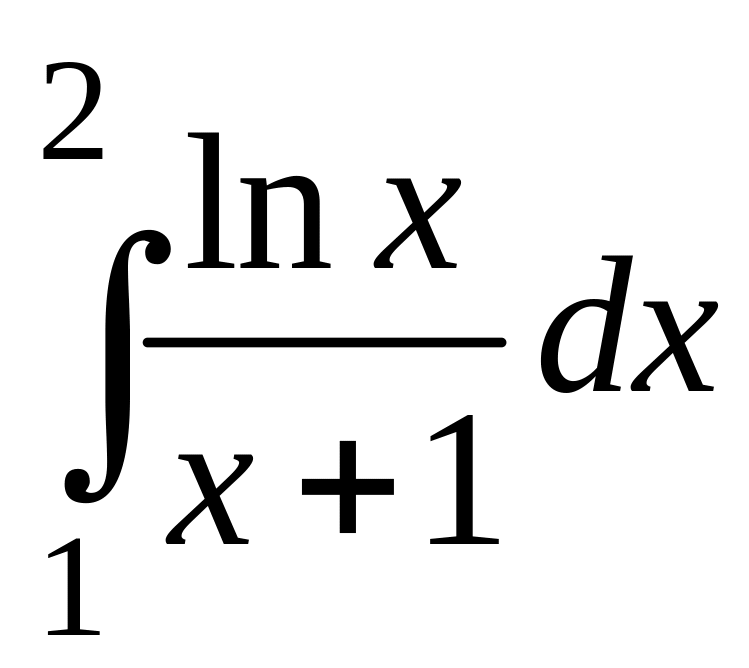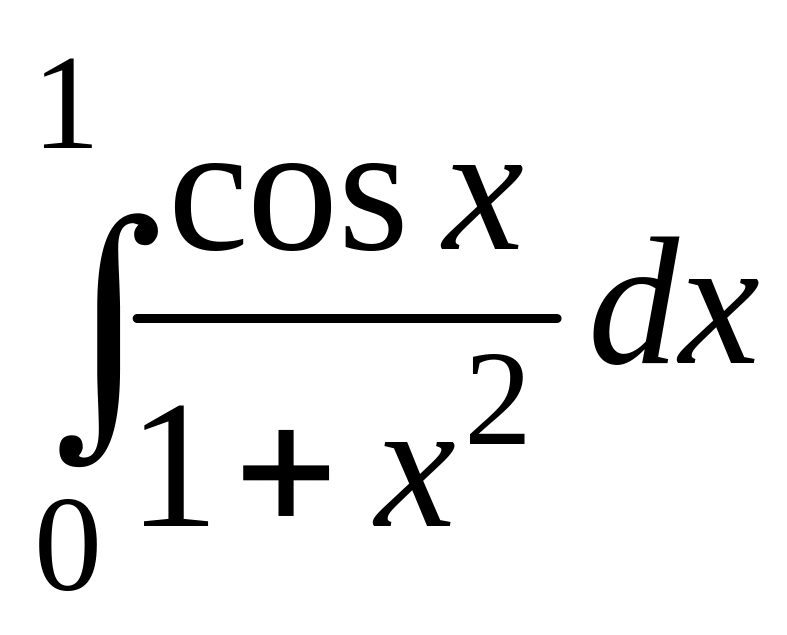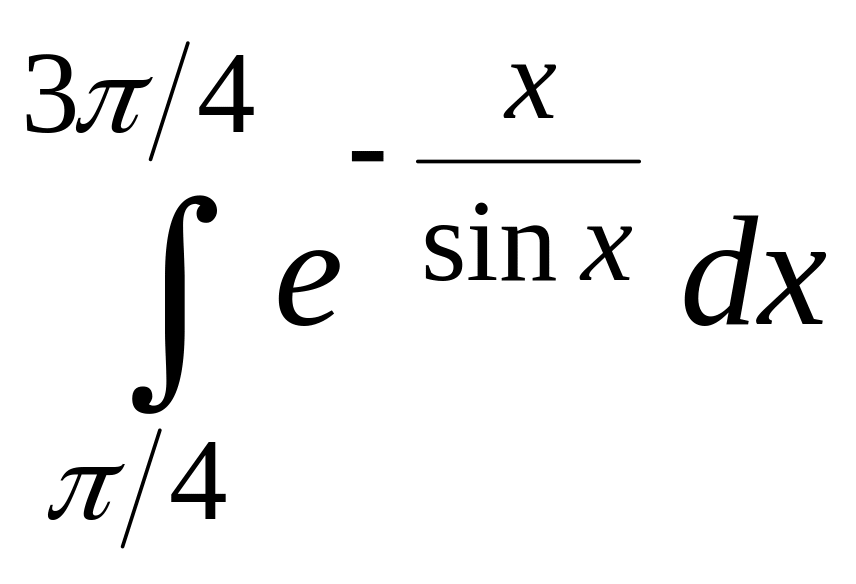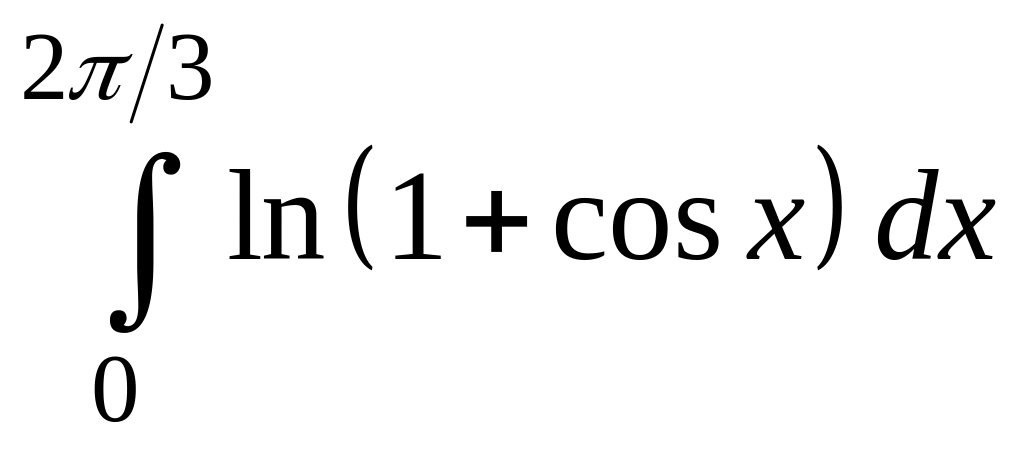Алгоритм программы
Задание констант x0
и 
;
описание переменных х, x1 и d;
описание функции 𝑓(х);
описание функции 
(х);
начало исполняемой части программы
присвоение начального приближения
переменной xl;
повторять
вывод на экран x1
и
d
с 7 цифрами после запятой до
выполнения условия
конец программы.
Контрольные вопросы
1. Как убедиться в том, что на отрезке имеются только один корень уравнения?
2. Опишите аналитический процесс нахождения корня методом касательных.
3. Дайте геометрическую интерпретацию метода для разных вариантов поведения функции: возрастающей, убывающей, вогнутой, выпуклой.
4. Как определить, в каком из концов дуги графика функции проводить касательную для получения приближения к корню?
5. Как оценить погрешность приближенного значения корня?
6. Как влияют численные значения первой и второй производной функции на скорость вычисления корня?
Содержание отчета
Отчет должен содержать постановку задачи, расчетную формулу, нахождение производных и вычисление их значений, проверку достаточных условий сходимости метода, обоснование выбора начального приближения, текст программы, вычисленные приближенные значения корня и соответствующие погрешности после каждой итерации.
Лабораторная работа № 3 приближенноевычисление определенных интегралов
Задание.
Вычислить интеграл 
методами
прямоугольников, трапеций и Симпсона с точностью
Краткое
описание методов: Вычисление
интеграла будем проводить параллельно
по трем формулам: прямоугольников,
трапеций и Симпсона. Процесс вычислений
будет закончен, когда требуемая точность
будет достигнута по одной из формул.
При этом отрезок интегрирования
первоначально разбивается на две равные
части, а в последующей итерации число
разбиений n увеличивается
в два раза. В
методе
прямоугольников
площадь элементарной криволинейной
трапеции приближенно заменяется площадью
прямоугольника. Методы прямоугольников
бывают трех видов:
метод
центральных прямоугольников, метод
левых прямоугольников и метод правых
прямоугольников.
В данной работе используется метод
левых прямоугольников, геометрическая
иллюстрация которого приведена на рис.
3. Соответствующая формула имеет вид
,
где
– величина шага разбиения отрезка 
.
ВВ
методе
трапеций
площадь элементарной криволинейной
трапеции приближенно заменяется площадью
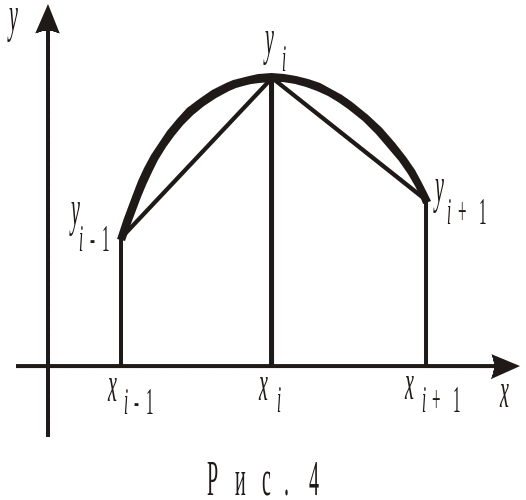
трапеции. Геометрическая иллюстрация
метода приведена на рис. 4. Соответствующая
формула для площади элементарной
криволинейной трапеции имеет вид 
.
Тогда вся площадь фигуры под кривой
В
методе
Симпсона
(методе парабол)
площадь элементарной криволинейной
трапеции заменяется площадью фигуры,
расположенной под параболой. Так как
число элементарных отрезков разбиения
четно, то в качестве элементарного
отрезка используется отрезок длины 2h
(рис.5). В
этом случае формула Симпсона имеет вид:
Отметим также, что формулы левых и правых прямоугольников имеют первый порядок точности относительно h, формулы центральных прямоугольников и трапеций имеют второй порядок точности, а формула Симпсона - четвертый порядок точности.
Варианты исходных данных
Ва- ри- ант |
Интеграл |
Ва- ри ант |
Интеграл |
1 |
|
13 |
|
2 |
|
14 |
|
3 |
|
15 |
|
4 |
|
16 |
|
5 |
|
17 |
|
6 |
|
18 |
|
7 |
|
19 |
|
8 |
|
20 |
|
9 |
|
21 |
|
10 |
|
22 |
|
11 |
|
23 |
|
12 |
|
24 |
|
Схема алгоритма метода.
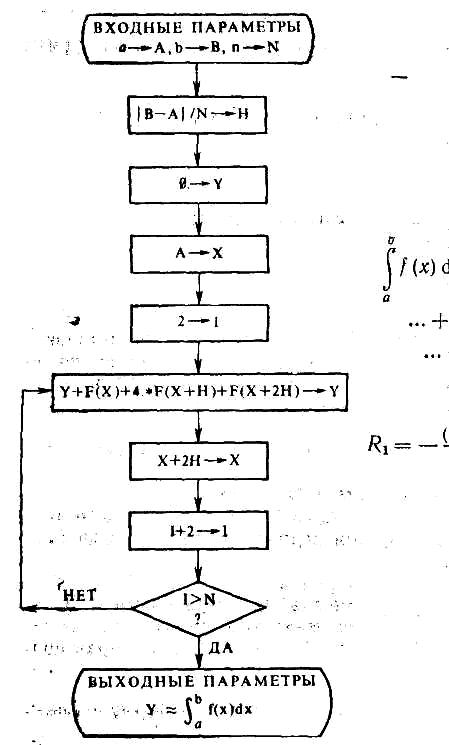
Алгоритм программы
Задание констант
а,
b
и
;
описание переменных х, Qn, Qs, h, Sp, St, SS, d, k, n;
описание подынтегральной функции 
;
начало исполняемой части программы
повторять
повторять
|
до выполнения условия
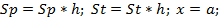
повторять
|
до выполнения условия
вывод на экран номера итерации k и значения Sp, St и SS с семью цифрами после запятой; до выполнения условия
.
конец программы.