Варианты исходных данных

Вариант	G(x)	C	D	[a,b]	h
1		-10	-35	[-1;8]	1,0
2		3	6	[-6;3]	1,0
3		-1	2	[-1;8]	1,0
4		11	-34	[-8;1]	1,0
5		10	-84	[-3;6]	1,0
6		0,3	-1	[-6;3]	1,0
7		-5	17	[1;10]	1,0
8		-1	3	[-2;7]	1,0
9		6	-12	[0,6;1,5]	0,1
10		5	-4	[0,1;1,0]	0,1
11		-3	10	[1,10]	1,0
12		-6	4	[0,1,1,0]	0,1
13		2	-10	[1,0;1,9]	0,1
14		-2	3	[0;9]	1,0
15		5	-6	[0,4;1,3]	0,1
16		0	-1	[1,8;2,7]	0,1
17		0	-2	[1,0;1,9]	0,1
18		-3	3	[1;2]	0,1
19		8	-80	[-3;2]	0,5
20		0,5	0	[1,0;1,9]	0,1
21		-1	-3	[1,0;1,9]	0,1
22		6	1	[0,5;1,4]	0,1
23		2,5	2	[-3;6]	1,0
24		0	-1	[0,1;0,9]	0,1

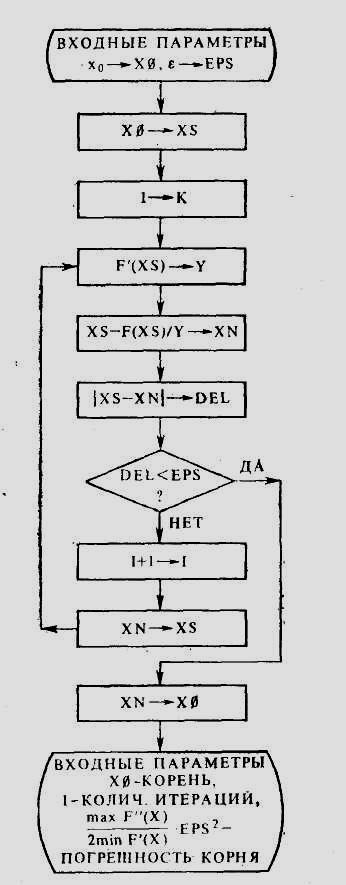
Схема алгоритма метода.

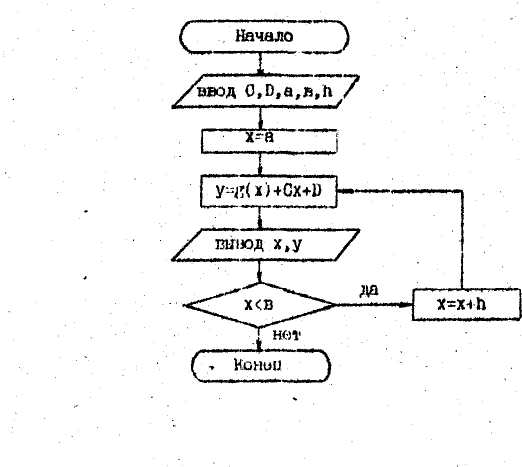
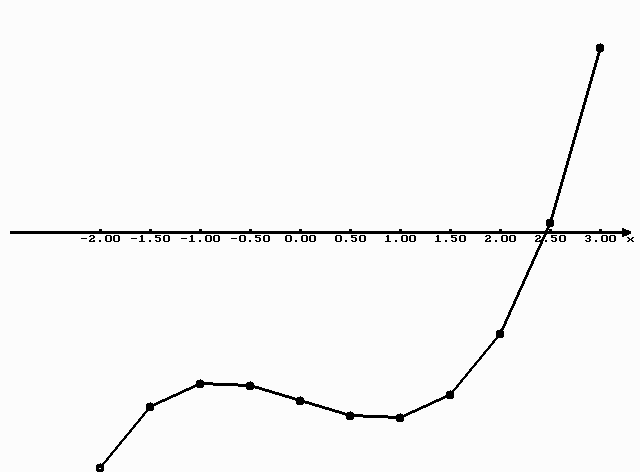
Приведем пример программы табулирования функции на отрезке [-2, 3] с шагом h=0,5 и ее график.

На экране появляются результаты табулирования:

x= -2.0000 x= -1.5000 x= -1.0000 x= -0.0000 x= 0.0000 x= 0.5000 x= 1.0000 x= 1.5000 x= 2.0000 x= 2.5000 x= 3.0000

y=-14.0000 y=-10.3750 y= -9.0000 y= -9.1250 y=-10.0000 y=-10.8750 y=-11.0000 y= -9.6250 y= -6.0000 y= 0.6250 y= 11.0000 max y=14.0000

Рис.1.

Из полученных значений функции и графика видно, что

функция меняет знак на отрезке [2,0; 2,5], а значит корень

уравнения расположен на этом отрезке.

Контрольные вопросы

1. В чем заключается табулирование функции на отрезке?

2. С какой целью используется табулирование функции и построение ее графика?

3. Как организован цикл для табулирования функции?

4. Как организован цикл для построения графика?

Содержание отчета

Отчет должен содержать постановку задачи, текст программы, результаты табулирования и график функции.

ЛАБОРАТОРНАЯ РАБОТА № 2

ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ

УРАВНЕНИЙ

Задание. Найти по методу Ньютона (методу касательных) приближенное значение корня уравнения с

точностью . Функция для каждого варианта та же, что и в лабораторной работе № 1.

Описание метода

Если известно хорошее начальное приближение решения уравнения , то эффективным методом повышения точности является метод Ньютона.

Он состоит в построении итерационной последовательности сходящейся к корню уравнения. Сформулируем достаточные условия сходимости метода.

Теорема. Пусть f(x)определена и дважды дифференцируема на [a,b], причем , а производные 𝑓'(х) и 𝑓"(x) сохраняют знак на [a,b]. Тогда, исходя из начального приближения , удовлетворяющего неравенству f( )f"( )>0 можно построить последовательность (2.1), сходящуюся к единственному на решению ξ уравнения f(x)=0.

Метод Ньютона допускает простую геометрическую интерпретацию (рис.2).

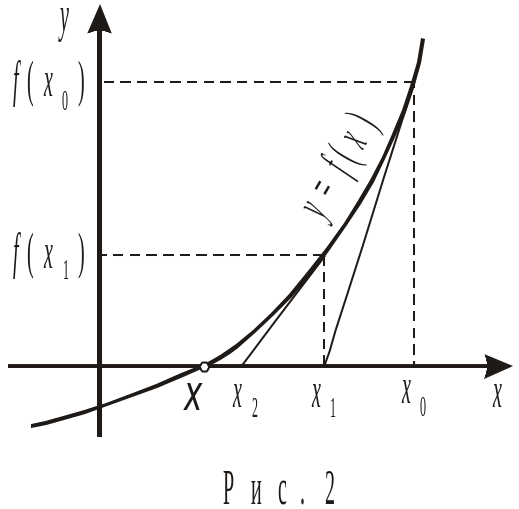
Через точку с координатами проводим касательную до пересечения с осью Ох. Абсцисса точки пересечения будет являться очередным приближением корня уравнения. Через точку с координатами тоже проводим касательную к графику функции и получаем очередное приближение . Продолжая далее этот процесс, получим последовательность точек . Из рисунка видно, что эта последовательность сходится к решению ξ уравнения . Для оценки погрешности n-го приближения корня можно воспользоваться неравенством , где , . Таким образом, если . Последнее соотношение означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро.

Порядок выполнения лабораторной работы

1. По результатам лабораторной работы № 1 определить отрезок [a,b], на котором функция меняет знак.

2. Убедиться, что на найденном отрезке функция удовлетворяет достаточным условиям сходимости метода Ньютона.

3. В качестве начального приближения х₀ взять тот конец отрезка [a,b], на котором выполняется

4. Составить программу по приведенному ниже алгоритму. В качестве критерия достижения точности принять выполнение неравенства .

Схема алгоритма метода