
- •Операции над комплексными числами.
- •2.1. Условие дифференцируемости функции комплексной переменной
- •2.2. Геометрический смысл аргумента и модуля производной
- •2.3. Гармонические функции
- •3. Элементарные функции комплексной переменной (кп)
- •3.1. Дробно-линейная функция
- •3. Рассмотрим общее дробно-линейное преобразование
- •3.3. Показательная функция и логарифм
- •4.Разложение функции комплексной переменной в ряды тейлора и лорана
- •4.1. Сходимость и равномерная сходимость
- •4.2. Свойства равномерно сходящихся рядов
- •4.3. Область сходимости степенного ряда
- •4.4. Ряд Тейлора
- •4.5. Способы разложения функций в ряд Тейлора
- •4.6. Ряд Лорана, разложение функций в ряд Лорана.
- •5. Вычеты и их приложения
- •Библиографический список
- •394026 Воронеж, Московский просп., 14
4.5. Способы разложения функций в ряд Тейлора
Естественный
и универсальный способ разложения
аналитической функции в ряд Тейлора
- это вычисление коэффициентов
по формулам
![]() или
или
![]() .
.
Пример:
разложить главную ветвь
![]() в степенной ряд в окрестности точки
в степенной ряд в окрестности точки
![]() .
Главная ветвь
.
Главная ветвь
![]() определяется условием
определяется условием
![]() ,
она имеет вид
,
она имеет вид
![]() .
.
В
качестве комплексной плоскости
рассматривается расширенная комплексная
плоскость (включая бесконечно удаленную
точку) с разрезом по полуоси
![]() .
Вычислим значения функции и ее
производных в точке
.
Вычислим значения функции и ее
производных в точке
![]() :
:
![]() ,
,
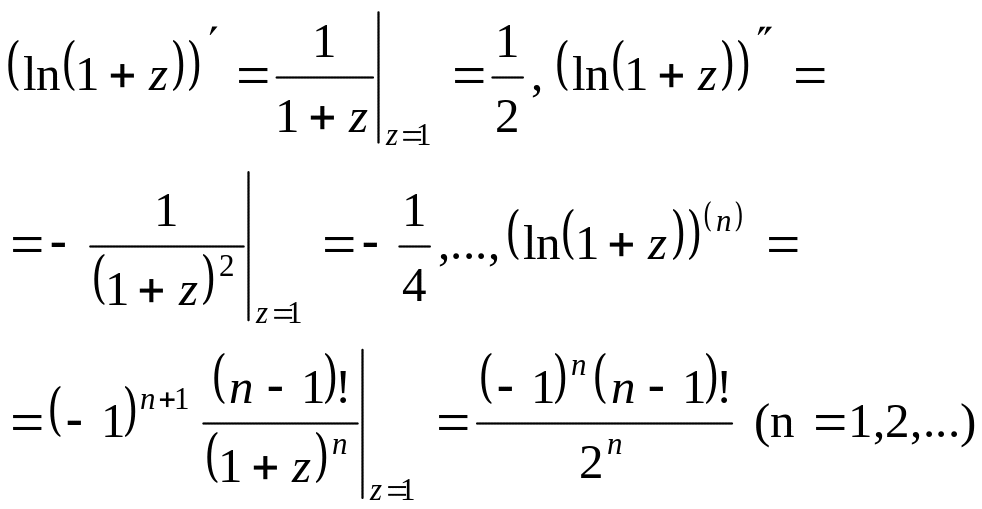
Следовательно, разложение имеет вид
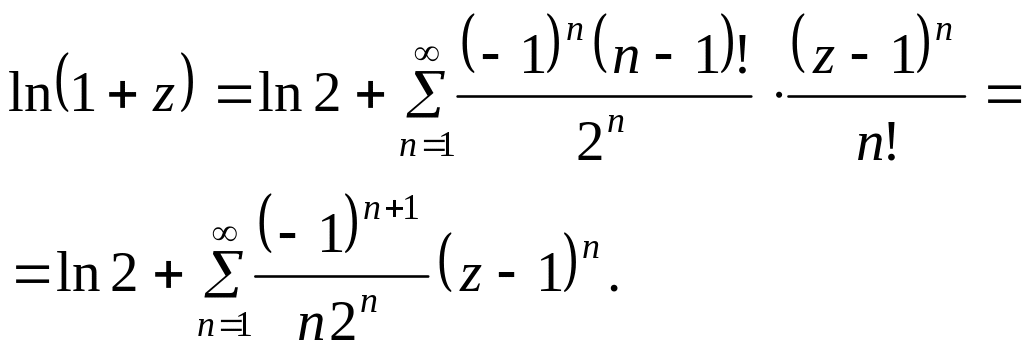
Часто
удается воспользоваться известными
табличными разложениями и не делать
громоздких вычислений связанных с
нахождением коэффициентов
.
Например, в предыдущем примере можно
было получить тот же результат проще,
вводя новую переменную
![]() и пользуясь табличным разложением для
логарифма:
и пользуясь табличным разложением для
логарифма:
![]()
![]()
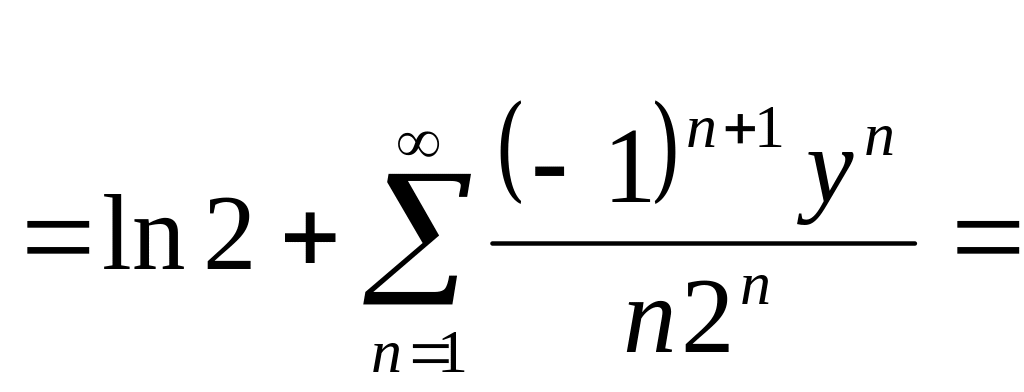
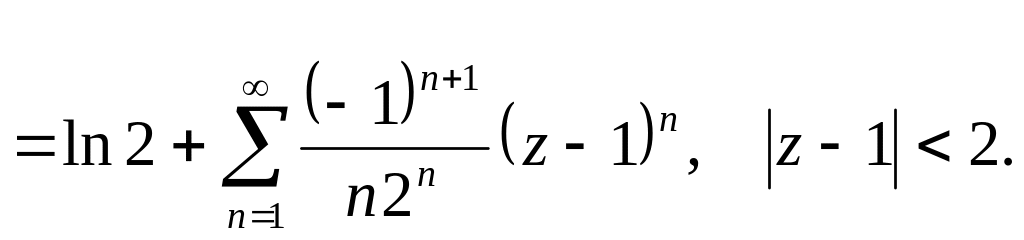
Существует
общий способ разложения функций, который
называется подстановкой ряда в ряд.
Пусть
![]() ,
причем
,
причем
![]() аналитична в круге
аналитична в круге
![]() ,
(тогда
,
(тогда
![]() ),
пусть
),
пусть
![]() аналитична в кpyre
аналитична в кpyre
![]() ,
(тогда
,
(тогда
![]() ,
коэффициенты разложения
,
коэффициенты разложения
![]() известны). Очевидно что
известны). Очевидно что
![]() ,
поэтому можно выбрать
,
поэтому можно выбрать
![]()
![]() такое, что при
такое, что при
![]() выполнено
выполнено
![]() ,
т.e.
принадлежит кругу
,
т.e.
принадлежит кругу
![]() - области аналитичности
.
Так как
аналитична в круге
,
то
- области аналитичности
.
Так как
аналитична в круге
,
то
![]() является аналитической в круге
и разлагается в нем по степеням
.
Следовательно,
является аналитической в круге
и разлагается в нем по степеням
.
Следовательно,
![]() .
.
Ряд
в правой части сходится равномерно в
круге
![]() ,
n
- кратное умножение возможно, так как
умножаются степенные ряды, а они сходятся
абсолютно в круге сходимости.
,
n
- кратное умножение возможно, так как
умножаются степенные ряды, а они сходятся
абсолютно в круге сходимости.
Таким
образом, выведено правило подстановки
ряда в ряд: для того, чтобы получить
разложение
в ряд Тейлора по степеням z , где
аналитична в окрестности
,
a
аналитична в окрестности
![]() ,
надо подставить ряд для
в ряд для
выполнить необходимые умножения рядов
и сложить коэффициенты членов, содержащих
одинаковые степени z. Полученный ряд
дает разложение
в ряд Тейлора и сходится в круге
,
надо подставить ряд для
в ряд для
выполнить необходимые умножения рядов
и сложить коэффициенты членов, содержащих
одинаковые степени z. Полученный ряд
дает разложение
в ряд Тейлора и сходится в круге
![]() ,
где
,
где
![]() выбирается так, чтобы при
было выполнено
выбирается так, чтобы при
было выполнено
![]() .
Заметим, что возможность получать
коэффициенты суммированием
следует из первой теоремы Вейерштрасса:
если
.
Заметим, что возможность получать
коэффициенты суммированием
следует из первой теоремы Вейерштрасса:
если![]() аналитична в
аналитична в
![]() ,
то
,
то
![]() .
.
Отсюда следует также возможность суммирования степенных рядов в общих областях сходимости.
Пример:
разложить в ряд по степеням z функцию
![]() .
.
Решеие:
Известно,
что
![]() .
В предыдущем примере получено разложение
.
В предыдущем примере получено разложение
![]() .
.
Подставляя ряд в ряд, получим
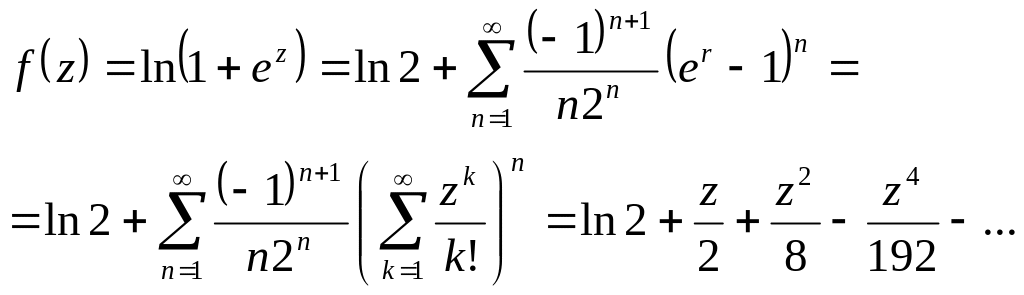 ,
,
где
;
выбирается из
![]() .
.
Примеры:
1. Разложить в ряд Тейлора по степеням z
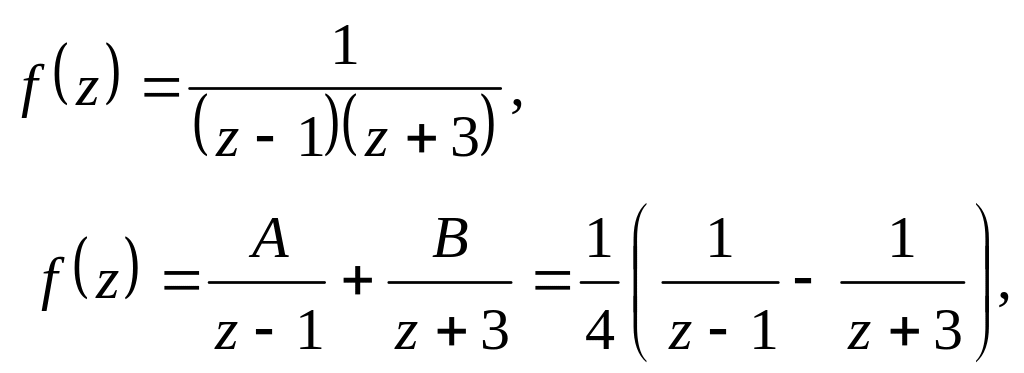
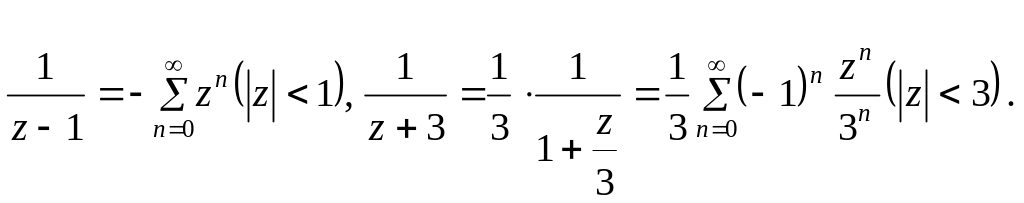
Область - общая область сходимости степенных рядов. Суммируя в этой области оба разложения, получим разложение в ряд Тейлора в круге :
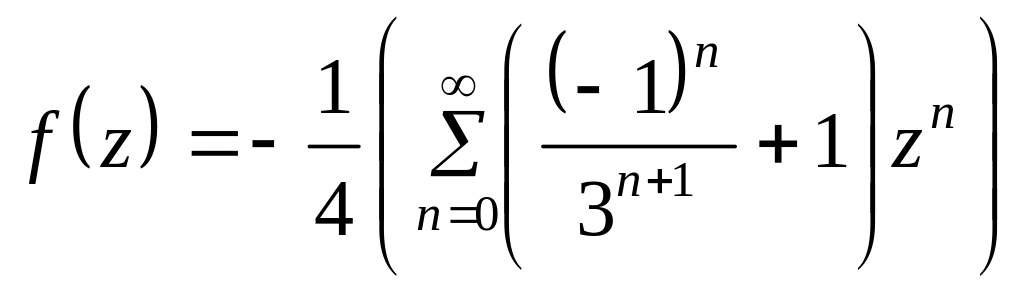 .
.
2.
Разложить в ряд Тейлора по степеням z
![]() .
.
Решение:
Здесь
удобнее дифференцировать ряд
![]() почленно
два раза:
почленно
два раза:
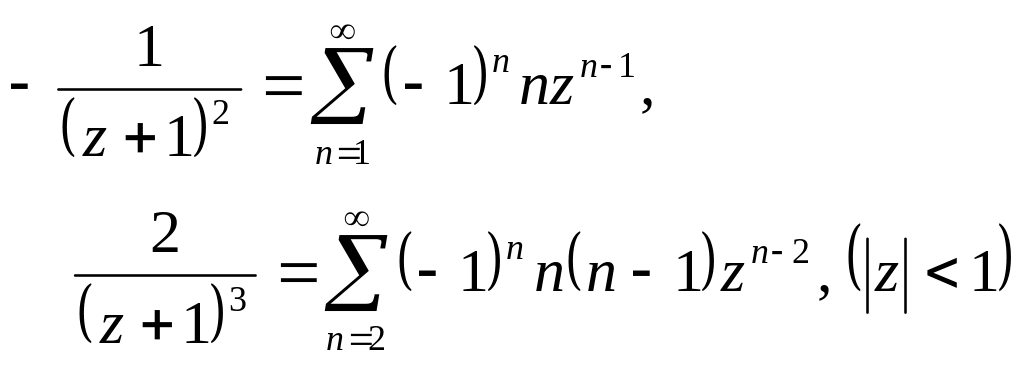 .
.
Упражнение: разложить в ряд по степеням z выписать три-четыре члена разложения
 ,
2)
,
2)
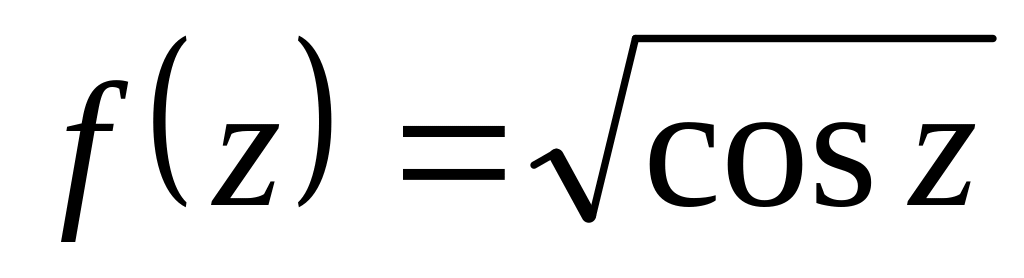 ,
3)
,
3)
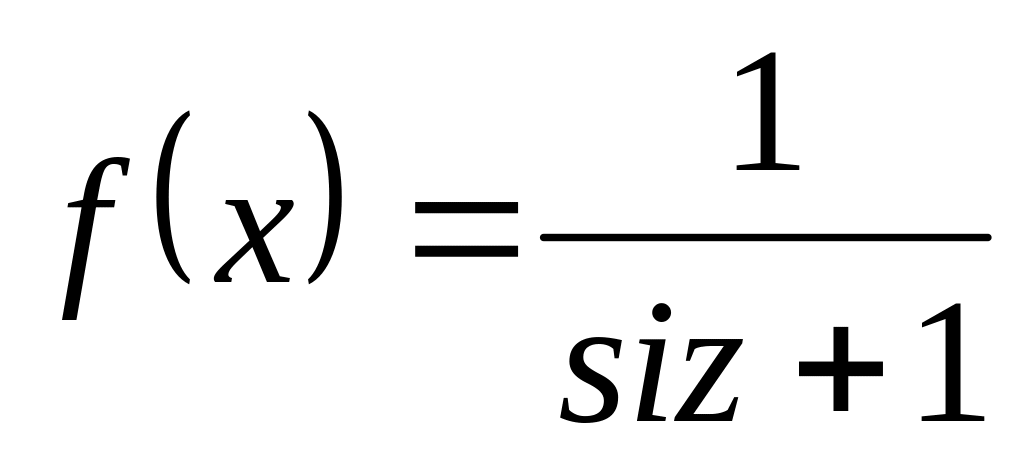 ,
,
4)
![]() ,
5)
,
5)
![]() ,
6)
,
6)
![]() .
.
4.6. Ряд Лорана, разложение функций в ряд Лорана.
Рядом
Лорана называется ряд
![]() .
.
Его
можно представить как сумму двух рядов:
- степенного ряда (правильная часть),
сходящегося
в круге
,
![]() - ряда по отрицательным степеням
- ряда по отрицательным степеням
![]() (главная часть). Если в главной части
сделать замену
(главная часть). Если в главной части
сделать замену
![]() ,
то главная часть перейдет в степенной
ряд
,
то главная часть перейдет в степенной
ряд
![]() сходящийся в некотором круге
сходящийся в некотором круге
![]() .
Если
,
то
.
Если
,
то
![]() ,
т.е. ряд
,
т.е. ряд
![]() сходится во внешности круга:
.
Следовательно, ряд
Лорана
сходится в круговом кольце
сходится во внешности круга:
.
Следовательно, ряд
Лорана
сходится в круговом кольце
![]() .
Если
.
Если
![]() или
или
![]() и на окружности
и на окружности
![]() нет общих точек сходимости главной
и правильной частей, то область сходимости
- пустое множество. Если
нет общих точек сходимости главной
и правильной частей, то область сходимости
- пустое множество. Если
![]() ,
но такие точки есть, то область сходимости
вырождается в совокупность точек или
дуги окружности. Если
,
но такие точки есть, то область сходимости
вырождается в совокупность точек или
дуги окружности. Если
![]() ,
то область сходимости представляет
собой круг с выколотым центром, а при
,
то область сходимости представляет
собой круг с выколотым центром, а при
![]() - внешность круга
- внешность круга
![]() .
Справедлива теорема Лорана: функция
.
Справедлива теорема Лорана: функция
![]() ,
аналитическая в кольце
,
представляется в нем сходящимся рядом
Лорана. Ряд Лорана равномерно сходится
в любом замкнутом кольце
,
аналитическая в кольце
,
представляется в нем сходящимся рядом
Лорана. Ряд Лорана равномерно сходится
в любом замкнутом кольце
![]() ,
целиком, содержащимся в исходном
,
целиком, содержащимся в исходном
![]() .
Сумма ряда Лорана является аналитической
функцией в кольце сходимости ряда
Лорана.
.
Сумма ряда Лорана является аналитической
функцией в кольце сходимости ряда
Лорана.
При
разложении в ряд Лорана можно использовать
внутри кольца сходимости суммирование
рядов, подстановку ряда в ряд, почленное
дифференцирование и интегрирование.
Коэффициенты ряда Лорана можно вычислить
по формуле, аналогичной соответствующей
формуле для
коэффициентов степенного ряда
![]() ,
где l –
кусочно-замкнутый контур, целиком
лежащий в кольце сходимости и охватывающий
точку
,
где l –
кусочно-замкнутый контур, целиком
лежащий в кольце сходимости и охватывающий
точку
![]() .
.
Пусть
ставится следующая задача: найти все
разложения
по степеням
![]() .
- задано.
.
- задано.
Первое,
что здесь необходимо сделать, это найти
все точки
![]() ,
в которых функция теряет аналитичность.
Если можно выбрать число С
такое, что, полагая
,
в которых функция теряет аналитичность.
Если можно выбрать число С
такое, что, полагая
![]() удаётся сделать функцию аналитической
в некоторой окрестности а
(здесь
удаётся сделать функцию аналитической
в некоторой окрестности а
(здесь
![]() - точка конечной плоскости), то такая
точка а
называется устранимой или правильной
точкой функции. Если такого С
не существует, но существует окрестность
точки a
, не содержащая других особых точек, то
такая точка а называется изолированной
особой точкой
функции однозначного характера (или
просто особой точкой). Например, точкам
для функции
- точка конечной плоскости), то такая
точка а
называется устранимой или правильной
точкой функции. Если такого С
не существует, но существует окрестность
точки a
, не содержащая других особых точек, то
такая точка а называется изолированной
особой точкой
функции однозначного характера (или
просто особой точкой). Например, точкам
для функции
![]() - устранимая точка.
Заметим, что
если a
- устранимая точка, то существует конечный
предел
- устранимая точка.
Заметим, что
если a
- устранимая точка, то существует конечный
предел
![]() .
Если этот предел бесконечен, то точка
а
называется полюсом функции, если предела
вообще не
существует, то точка а
называется существенно особой точкой
функции. Можно
показать, что разложение в ряд Лорана
в окрестности особой точки a:
.
Если этот предел бесконечен, то точка
а
называется полюсом функции, если предела
вообще не
существует, то точка а
называется существенно особой точкой
функции. Можно
показать, что разложение в ряд Лорана
в окрестности особой точки a:
а) не содержит главной части, если а - устранимая;
б)
содержит член
![]() ,
но не содержит члены
,
но не содержит члены
![]() низших степеней,
низших степеней,
![]() ,
если a
- полюс k-го
порядка (т.е. a
– нуль k-го
порядка функции
,
если a
- полюс k-го
порядка (т.е. a
– нуль k-го
порядка функции
![]() );
);
в)
содержит бесконечное количество членов
с отрицательными степенями
![]() ,
если a
- существенно особая точка функции.
,
если a
- существенно особая точка функции.
Предположи,
все особые точки
![]() функции найдены. Заметим, что бесконечно
удаленная точка всегда считается особой
и анализируется отдельно, причем анализ
может быть проведен аналогично, только
вместо членов с отрицательней степенями
надо рассматривать члены с положительными
степенями. После того, как все особые
точки найдены, надо провести на комплексной
плоскости концентрические окружности
с центром в точке
и радиусами, равными расстояниям от
точки
до особых точек
,
функции найдены. Заметим, что бесконечно
удаленная точка всегда считается особой
и анализируется отдельно, причем анализ
может быть проведен аналогично, только
вместо членов с отрицательней степенями
надо рассматривать члены с положительными
степенями. После того, как все особые
точки найдены, надо провести на комплексной
плоскости концентрические окружности
с центром в точке
и радиусами, равными расстояниям от
точки
до особых точек
,
![]() .
В каждом из образовавшихся круговых
колец функция
аналитична, и разлагается в свой ряд
Лорана, ряды в различных круговых
кольцах, как правило, различны. Если
функция представлена в виде суммы
функций (обычно специально разлагают
функцию в сумму более простых функций),
то надо построить разложения
функций-слагаемых во всех круговых
кольцах и суммированием получить
разложение функции-суммы.
.
В каждом из образовавшихся круговых
колец функция
аналитична, и разлагается в свой ряд
Лорана, ряды в различных круговых
кольцах, как правило, различны. Если
функция представлена в виде суммы
функций (обычно специально разлагают
функцию в сумму более простых функций),
то надо построить разложения
функций-слагаемых во всех круговых
кольцах и суммированием получить
разложение функции-суммы.
Примеры.
I. Найти все разложения функции
по степеням
![]() .
.
Решение:
Особая
точка
- полюс первого порядка, имеются две
области разложения:
-
область 1 и
![]() - область 2.
Выпишем разложение:
- область 2.
Выпишем разложение:
![]() при
,
т.е. в области 1,
при
,
т.е. в области 1,
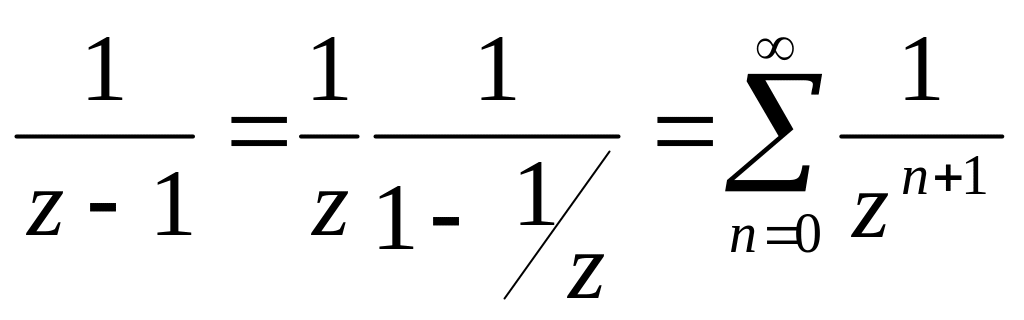 при
,
т.е. в области 2.
при
,
т.е. в области 2.
2. Найти разложения функции по степеням ,
Решение:
![]() .
.
Имеются
три области разложения:
- область 1,
![]() - область 2,
- область 2,
![]() - область 3.
- область 3.
![]() ,
,
![]() .
.
В области I получим разложение
![]() ,
,
в области 2 получим разложение
![]() ,
,
в области 3 получим разложение
![]() .
.
3.
Найти все разложения функции
по степеням
![]() ,
,
![]() .
.
Решение:
Здесь одна область разложения, так как - единственная особая точка. Вводя новую переменную , используем табличное разложение для экспоненты:
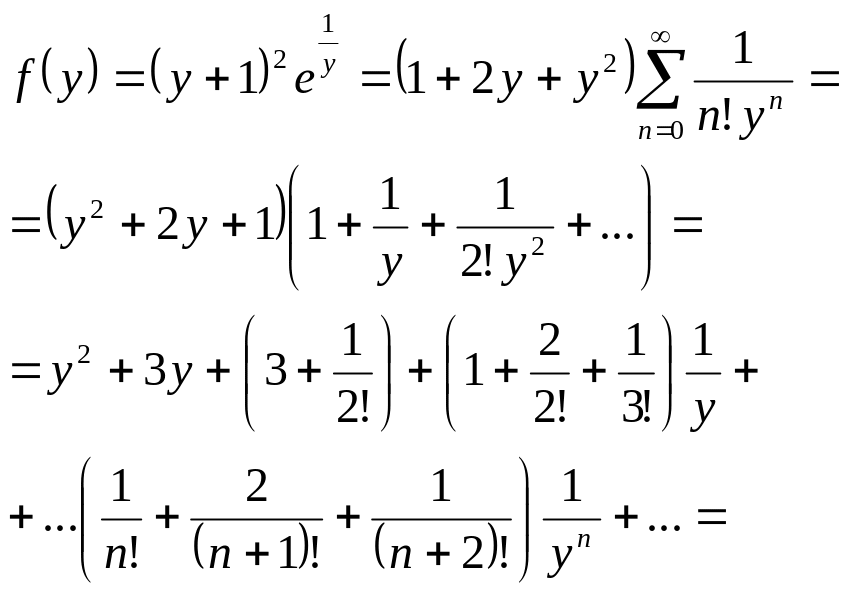
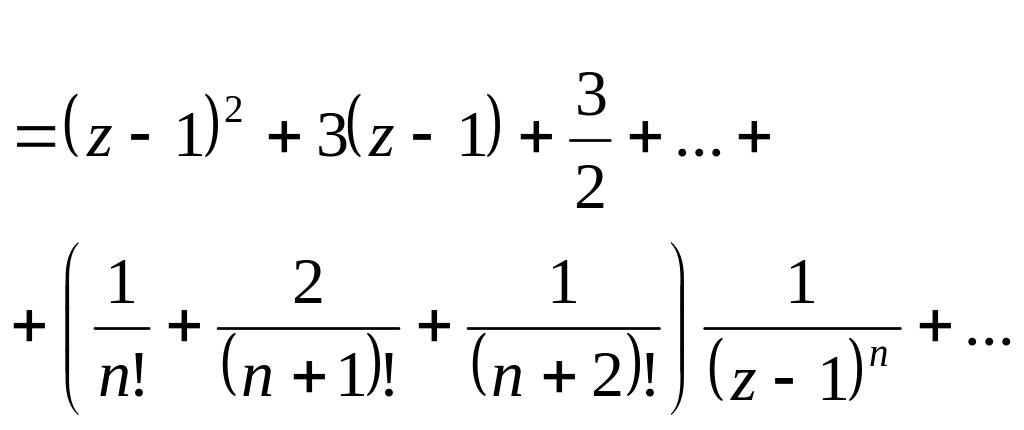
Это
и есть
разложение функции в кольце
![]() .
.
Упражнение: найти все разложения по степеням
1)
![]() ;
;
2)
![]() ;
;
3)![]() ;
;
4)
![]() ;
;
5)
![]()
