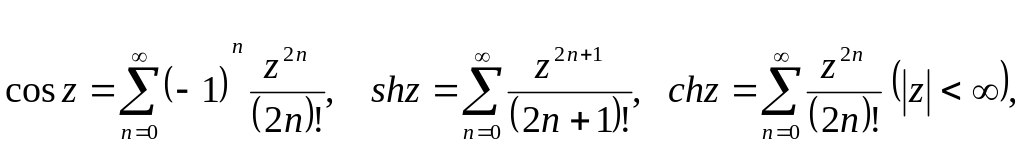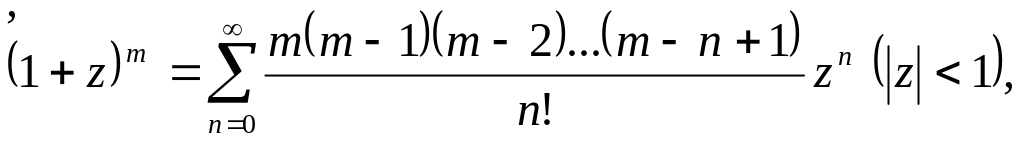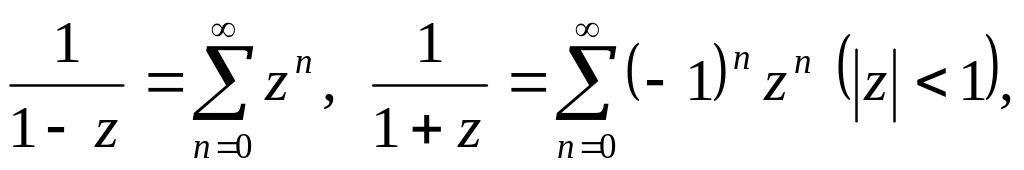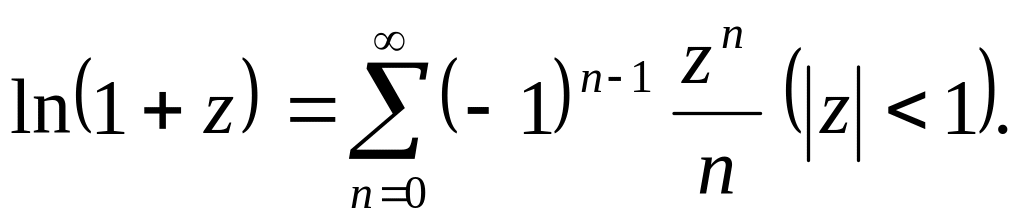4.2. Свойства равномерно сходящихся рядов

1. Если все члены функционального ряда непрерывны в области D и ряд равномерно сходится в D, то сумма ряда непрерывна в D (теорема о непрерывности сум­мы равномерно сходящегося ряда).

2. Пусть ряд равномерно сходится в D к , функции непрерывны в D при любом n, пусть кусочно-гладкий контур l целиком лежит в D. Тогда

(теорема о почленном интегрировании).

З. Пусть ряд равномерно сходится в любой замкнутой подобласти области D, функции анали­тические в D. Тогда

а) - сумма ряда - есть аналитическая функция в D;

б)

в) ряд сходится равномерно в любой подобласти области D (первая теорема Вейерштрасса).

4. Пусть ряд равномерно сходится на границе Г области D , - аналитические функции в открытой области D и непрерывные в замкнутой области D. Тогда ряд равномерно сходится в области D (вторая теорема Вейерштрасса).

4.3. Область сходимости степенного ряда

Функциональный ряд вида называется степен­ным. Очевидно, при любых ряд сходится в точке . Точка называется центром сходимости степенного ряда. Оказывается, что степенной ряд сходится в круге , где R - радиус сходимости степенного ряда. Это - следствие теоремы Абеля, которая формулируется следующим образом: если степенной ряд сходится в точке , то он абсолютно сходится в круге . Радиус сходимости степенного ряда можно найти, рассматривая ряд из модулей и применяя один из признаков сходи­мости знакопостоянных рядов, например признак Даламбера или радикальный признак Коши, как это было сделано в примерах п. 4.1. Сходимость на границе круга исследуется отдельно. Если ряд сходится, то степенной ряд сходится на всей грани­це. Если ряд расходится и не стремиться к 0, то ряд расходится во всех точках границы. Если ряд расходится, но , , то ряд может сходиться в одних точках границы и расходиться в других; в этом случае надо выделять ряды из действительных и мнимых частей и исследо­вать каждый из них.

Пример: определить область сходимости ряда и проанализировать его сходимость в точках .

Решение:

Найдем радиус сходимости ряда, рассматривая ряд из модулей и применяя признак Даламбера:

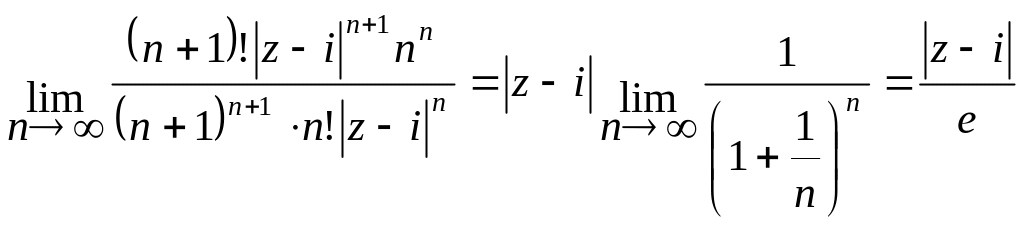
Ряд сходится в круге . Подставим в ряд из модулей , получим расходящийся ряд . Проверим необходимый признак сходимости ряда из модулей на границе круга:

Следовательно, ряд может сходиться в одних точках границы и расходиться в других. Подставим в ряд, получим - расходящийся ряд. Подставляя в ряд, получим ряд - сходящийся по признаку Лейбница. Подставим в ряд, получим

.

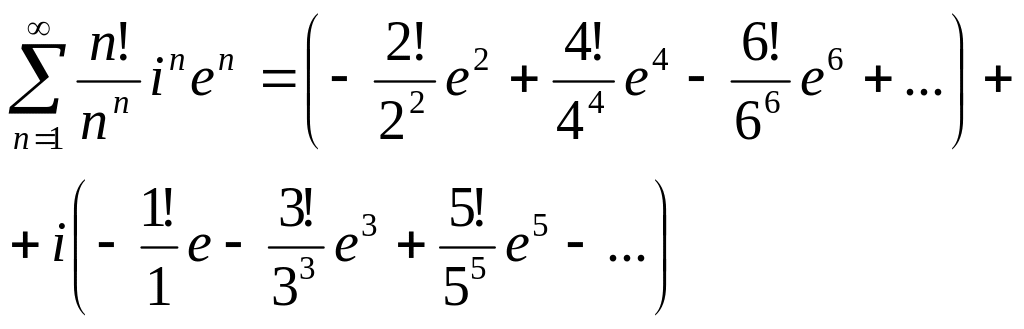Ряд из действительных и мнимых частей сходится по признаку Лейбница.

4.4. Ряд Тейлора

Можно показать, что степенной ряд равномерно сходится в круге , поэтому к нему могут быть применены теоремы п. 4.2, в частности, первая теорема Вейерштрасса.

Следовательно, всякий степенной ряд внутри своего круга сходимости сходится к некоторой аналитической функции , причем можно найти, дифференцируя степенной ряд почленно k раз. Дифференцируя ряд , получим

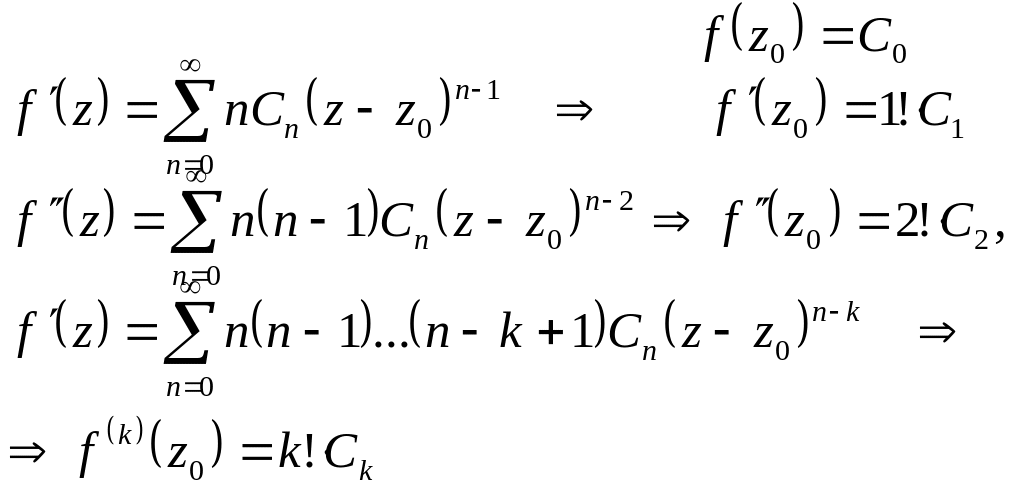
Таким образом, подставляя коэффициенты в ряд, получим

- ряд Тейлора функции . Итак, всякий сходящийся степенной ряд есть ряд Тейлора своей суммы. При ряд Тейлора называется рядом Маклорена.

Справедлива теорема о разложении аналитической функции в степенной ряд: функция , аналитическая в круге , разлагается в кем в степенной ряд , где коэффициенты можно вычислять по формулам или . В этих формулах l – любой кусочно-гладкий замкнутый контур, целиком лежащий в круге и охватывающий точку . Для коэффициентов ряда справедливы неравенства Коши , где ; - окружность . Приведем разложения в ряды Маклорена наиболее часто встречающихся функций: