4.Разложение функции комплексной переменной в ряды тейлора и лорана
4.1. Сходимость и равномерная сходимость
Исследование
рядов с комплексными членами во многом
аналогично исследованию рядов с
действительными членами. Известно,
например, что ряд
,
где
- комплексные числа, сходится тогда и
только тогда, когда сходятся оба ряда;
из действительных
и
мнимых
частей. Поэтому исследование ряда с
комплексными членами сводится к
исследованию пары рядов с действительными
членами.
Формулируя
критерий Коши для последовательности
частичных сумм ряда
,
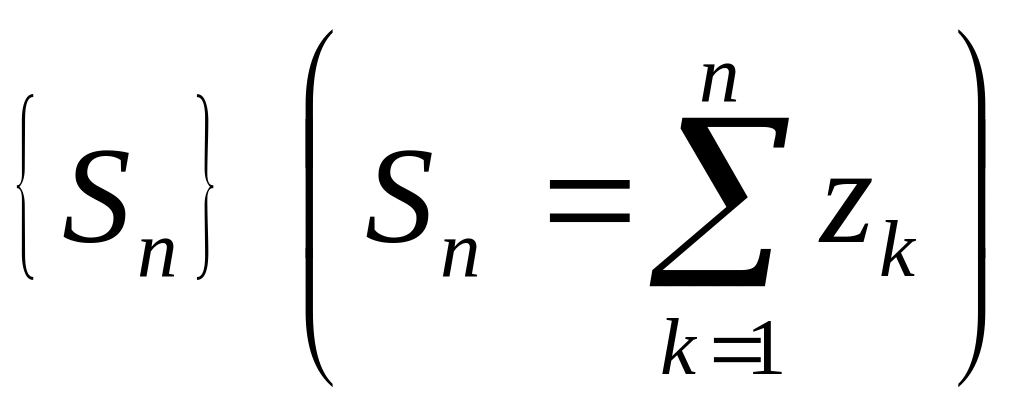получим критерий Коши сходимости ряда:
ряд сходится тогда и только тогда, когда
для любого
существует такое
,
что неравенство
выполняется при любом
и любом натуральном p.
Можно
сформулировать критерий сходимости
ряда, вводя остаток ряда
:
ряд сходится тогда и только тогда, когда
Примеры. 1. Исследовать на сходимость ряд
.
Решение:
Ряд
из действительных
частей
и
мнимых частей
абсолютно сходятся, следовательно,
исходный ряд сходится.
В
этом примере достаточно сразу исследовать
ряд
:
,
ряд
сходится, поэтому члены рядов из
действительных и мнимых частей
мажорируются членами сходящегося ряда
из модулей.
2.
Исследовать на сходимость ряд
.
Здесь абсолютной сходимости нет, но ряды из действительных и мнимых частей сходятся по признаку Лейбница, следовательно ряд сходится.
3.
Исследовать на сходимость ряд
.
Здесь оба ряда из действительных и мнимых частей расходятся, следовательно, ряд расходится.
Если
члены ряда являются функциями комплексной
переменной, то имеем функциональный
ряд
.
Если выбрать конкретное значение
,
то получим числовой ряд
,
который сходится или расходится.
Множество точек z, в которых ряд сходится,
составляет область сходимости
функционального ряда.
Среди функциональных рядов выделяется класс рядов, близкий по свойствам к числовым рядам - равномерно сходящиеся ряды.
Ряд
называется равномерно сходящимся в
области D к функции
,
если для любого
найдется такой номер
,
при котором для любого
и любого
выполнено
.
Числовые сходящиеся ряды, очевидно,
равномерно сходятся в любой области.
Можно сформулировать критерий Коши
равномерной сходимости функционального
ряда: ряд равномерно сходится в области
D тогда и только тогда, когда для любого
существует
такое
,
что неравенство
выполняется при любом
,
любом натуральном p
при всех
.
Критерий равномерной сходимости можно
сформулировать, вводя остаток ряда: ряд
равномерно сходится в области D тогда
и только тогда, когда
.
Если
ряд сходится, но не равномерно, то
,
но
(
)
либо не
существует, либо не равен нулю. Равномерную
сходимость ряда часто легко установить,
пользуясь признаком равномерной
сходимости Вейерштрасса: пусть дан
функциональный ряд
,
причем числовой ряд
сходится.
Тогда функциональный ряд
сходится равномерно в области D.
Пример:
исследовать ряд
на сходимость.
Решение:
Рассмотрим ряд из модулей , применим к нему признак Даламбера:
.
Ряд
сходится при
.
В любой граничной точке z,
ряд мажорируется сходящимся рядом
поэтому область сходимости ряда.
.
В этой области ряд сходится равномерно,
так как в любой области исходный ряд
мажорируется рядом
.
Пример:
исследовать
на сходимость
ряд
(геометрическая прогрессия).
Решение:
Рассматривая
ряд из модулей, применим радикальный
признак Коши или признак Даламбера.
Оказывается, что ряд сходится при
,
но расходится при
.
Так как
никогда
не стремиться к 0 при
,
то необходимый признак сходимости ряда
не выполнен. Ясно, что
сумма ряда
,
при
,
остаток ряда
,
поэтому ряд не сходится равномерно в .