3. Рассмотрим общее дробно-линейное преобразование

,считая .

ФКП W осуществляет взаимно-однозначное отображение , так как

, .

Нетрудно видеть, что общее дробно-линейное отображение можно получить, последовательно осуществляя линейные отображения и отображение :

. (14)

Из (14) получаем последовательность отображений:

1) ;

2) ;

3) ,

т.е. два линейных отображения и одно типа .

Следовательно, если какое-либо свойство присуще линейному и отображению, то это же свойство будет характерным и для дробно-линейного отображения.

Докажем, что дробно-линейное отображение обладает круговым свойством: окружности, принадлежащие плоскости преобразу­ются в окружности, принадлежащие плоскости W . При этом прямые считаем окружностями бесконечно большого радиуса.

Убедимся в том, что отображение обладает круговым свойством:

, ,

,

.

Уравнение семейства окружностей на записывается в виде

.

Уравнение образа этого семейства на плоскости W

Рассмотрим на плоскости точку . При отображении . Следовательно, образ каждой прямой или окружности, проходящей в плоскости через точку , содержит точку , т.е. все прямые и окружности, проходящие в плоскости через точку , переходят в прямые на плоскости W. Все прямые и окружности, не проходящие через , в плоскости W являются окружностями, так как ни одна точка их прообразов не перейдет в точку .

Пример: отобразить конформно верхнюю полуплоскость на внутренность круга так, чтобы граница полуплоскости перешла в окружность . Дробно-линейное отображение обладает круговым свойством, поэтому для решения поставленной задачи достаточно так подобрать коэффициенты функции , чтобы установить соответствие между выбранными точками оси ( ) и наперед заданными точками окружности . Пусть , тогда

,

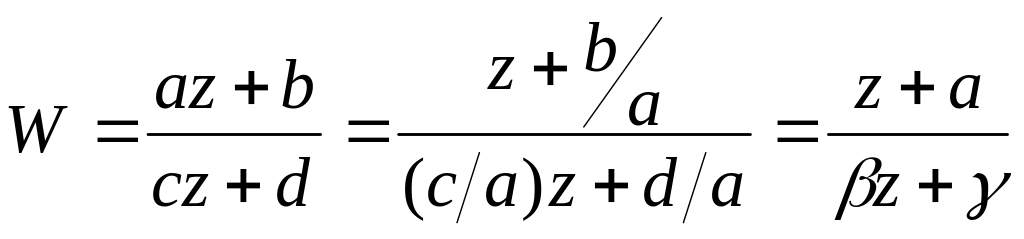т.е. для задания дробно-линейного отображения достаточно знать три параметра чего необходимо задать соответствие

.

Например, так подберем чтобы

y

v

i

(рис. 6)

x

0

-1

1

u

0

-1

1

-i

Из (16) имеем (k = I, 2, 3). Отсюда для нахождения получим систему трех линей­ных уравнений:

Отсюда , , .

Таким образом .

3.2. Степенная функция

Изучим некоторые свойства отображения, осуществляемого функцией .

Представим числа z и W в тригонометрической форме:

(17)

По формуле Муавра

(18)

Отсюда видно, что при отображении с помощью степенной функции происходит поворот каждого вектора на угол и растяжение в раз. Легко проверяется следующее утверж­дение: если две точки и плоскости Z таковы, что , то их образы и равны.

Поэтому для выделения областей плоскости (т.), для точек которых степенная функция осуществляет взаимно-однозначное отображение, необходимо потребовать, чтобы область не содержала точек с аргументами, отличающимися на целое кратное .

Р

x

x

y

Θ

φ

W=zⁿ

ис. 7.

u

nφ

nΘ

Такими областями на являются углы (рис. 7)

(к=0, I, ...) (19)

Области, для точек которых данная функция осуществляет взаимно-однозначное отображение, называются областями однолистности данного отображения (функции).

Следовательно, области (19) являются областями однолистности отображения, задаваемого степенной функцией .

Н

y

C

D

γ

W=z²

а примере отображения посредством функции введем одно важное понятие. Из предыдущего следует, что областями однолистности для данной функции на плоскости являются полуплоскости (рис. 8). Очевидно, что левая и правая полуоси ОХ как стороны угла переходят в лучи и на плоскости W , т.е. в полуось. ReW=0.

x

0

1

-1

B

A

v

C’

A’

γ*

Рис. 8.

v

B’

D’

Чтобы для всех точек полуплоскости сохранить условие однолистности отображения, мысленно разрежем плоскость W по полуоси и слегка сместим края разреза (в плоскости W). Получим геометрическое представление о плоскости с разрезом по оси 0u.

Пользуясь этим примером, можно объяснить происхождение термина однолистность: для отображения точек верхней полуплоскости потребовалась целая плоскость w (один лист); для отобра­жения всех точек плоскости z потребуется еще одна плоскость (лист).

Будем говорить, что луч переходит в верхний берег разреза, луч - в нижний берег разреза.

Вообще, если , то каждый из углов плоскости z отображается в плоскость с разрезом, а вся плоскость z отображается в n-листную плоскость w.

Отметим, что изучаемое отображение (n - целое положи­тельное) конформно всюду, кроме точки (см. пример в п.2):

. (20)

Используя методы анализа, можно вывести аналогичную (20) формулу для любого действительного показателя r : ,

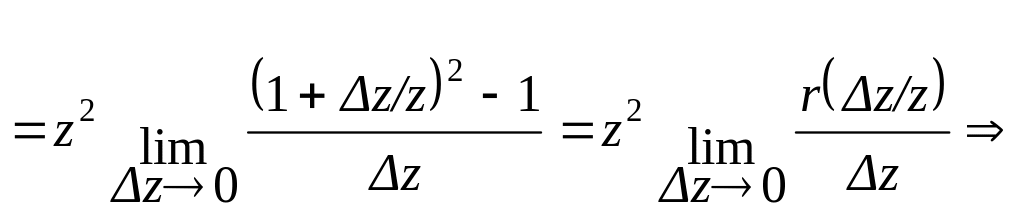
(20’)

Функция, обратная к , называется корнем n-й степени и записывается в виде . Число W называется корнем n-й степени из числа z, если .

В алгебре комплексных чисел было выяснено, что корень n-й степени из числа z имеет n различных значений.

Следовательно, функция n-значна: .

Значение определяется значением аргумента, выбранным для точки z (вспомним, что значение аргумента числа z определяется с точностью до ).

Обозначим через одно из значений аргумента точки и предположим, что точка описывает замкнутую кривую С на плоскости Zтак, что начало координат остается вне области D границей которой является С (рис. 9). Через обозначим значения аргументов точек .

L

Z₀

c

x

y

W₀

Ĺ

v

Ć₃

Ć₁

Ć₂

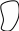
Рис. 9.

Очевидно, при обходе контура C меняется непрерывно от и при полном обходе контура C принимает прежнее значение, равное .

Следовательно, в плоскости W точка

,

описывая замкнутую кривую ,начиная от точки

,

вернется к своему прежнему значению .

Значения корня, определяемые другим выбором аргумента /например, (к = I, 2,...)/ при полном обходе по кривой С также описывают замкнутые кривые , отличающиеся от C лишь поворотом на .

Теперь рассмотрим кривую внутренность, которой содержит точку (см. на рис. 9 пунктир).

При полном обходе кривой L от точки со значением аргумента соответствующая точка не возвращается в положение , а занимает новое положение,

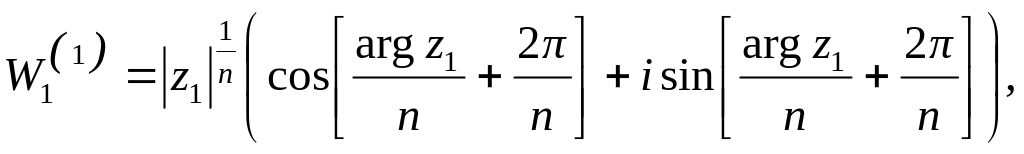так как аргумент точки при полном обходе по L получил приращение своему начальному значению , точка вернется лишь при n-кратном обходе кривой L , поскольку в этом случае аргумент точки , получит приращение .

На рис. 9 показан случай n=3.

Отсюда следует, что в любой области , не содержащей ни одной кривой, обходящей точку , можно выделить n непрерывных и однозначных функций, принимающих одно из значений корня .

Эти n функций называются ветвями многозначной функции ; их значения для каждого фиксированного z отличаются друг от друга множителями .

В этом случае каждая из ветвей является непрерывной функцией и осуществляет однолистное (взаимно однозначное) отображение области D. Поэтому каждой точке области D применима теорема о производной обратной функции

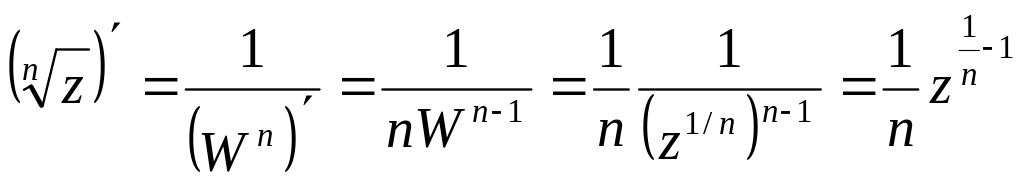
Если область в плоскости z содержит хотя бы одну кривую, об­ходящую точку , то ветви отделить нельзя, они непрерывно переходят одна в другую.

Сравните на рис. 9 кривые .