4.1.3.Плоскопараллельное движение твердого тела

Движение твердого тела называется плоскопараллельным (или плоским), если все точки тела перемещаются в плоскостях, параллельных некоторой фиксированной плоскости (основной плоскости).

На рис. 4.2 изображено некоторое тело V, совершающее плоское движение ( - основная плоскость).

Частным случаем плоского движения является вращение твердого тела вокруг неподвижной оси: все точки вращающегося тела движутся в плоскостях, параллельных некоторой перпендикулярной оси вращения неподвижной плоскости.

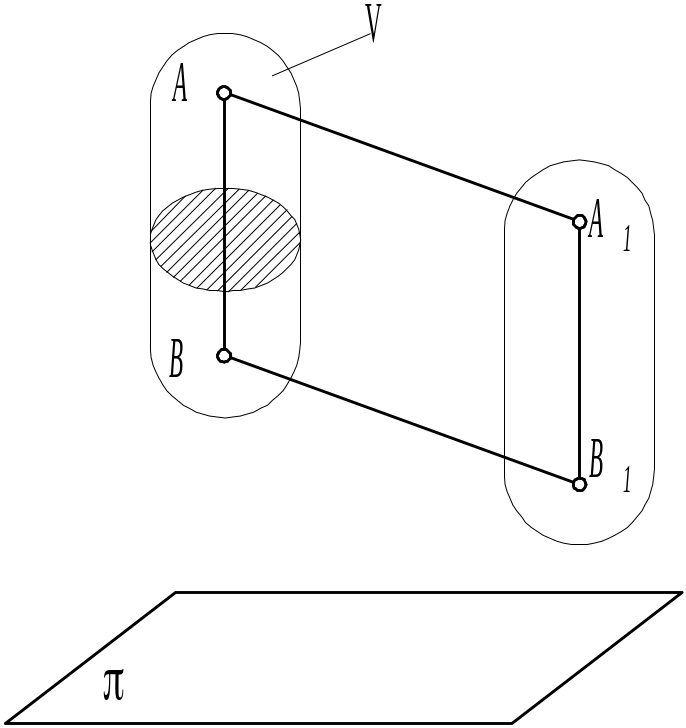
Рис. 4.20

Качение колеса по прямолинейному отрезку рельса тоже является плоскопараллельным движением, так как все его точки перемещаются в плоскостях, параллельных плоскости, перпендикулярной оси колеса.

4.1.4.Разложение плоскопараллельного движения на поступательное и вращательное

Пусть некоторое тело совершает плоскопараллельное движение. Рассмотрим некоторое параллельное основной плоскости сечение этого тела.

Произвольно выбранную точку сечения (или плоскости, которой принадлежит сечение и которая неизменно связана с сечением) называют полюсом.

Теорема: Всякое перемещение плоской фигуры в ее плоскости может быть составлено из поступательного перемещения фигуры вместе с некоторым полюсом и поворота вокруг этого полюса.

4.1.5.Скорость точки плоской фигуры

Теорема: Скорость V_B любой точки В плоской фигуры (рис. 4.3) в данный момент времени есть геометрическая сумма скорости V_A некоторого полюса А и скорости V_BA, возникающей вследствие вращения фигуры вокруг полюса, т.е.:

V_B=V_A+V_BA. (4.2)

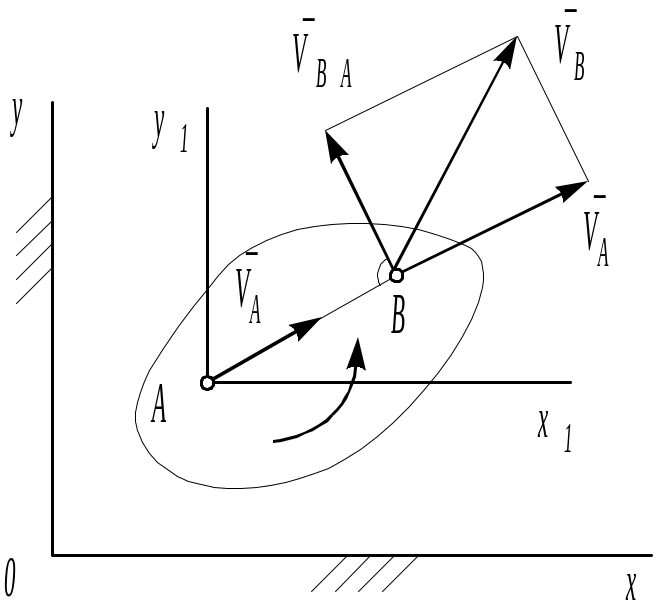
Рис. 4.21

Теорема: Проекции скоростей двух точек плоской фигуры на ось, проходящую через эти точки, равны между собой.

4.1.6.Мгновенный центр скоростей и распределение скоростей точек плоской фигуры

Мгновенным центром скоростей (м.ц.с.) называется такая точка плоской фигуры (или неизменно связанной с этой фигурой плоскости), скорость которой в данный момент времени равна нулю.

Скорости точек плоской фигуры в данный момент времени распределены таким образом, как если бы эта фигура вращалась вокруг мгновенного центра скоростей с угловой скоростью  (рис. 4.4).

Рис. 4.22

Рассмотрим способы нахождения мгновенного центра скоростей.

а) Пусть заданы направления скоростей двух точек А и В, причем векторы V_A и V_B не параллельны (рис. 4.5).

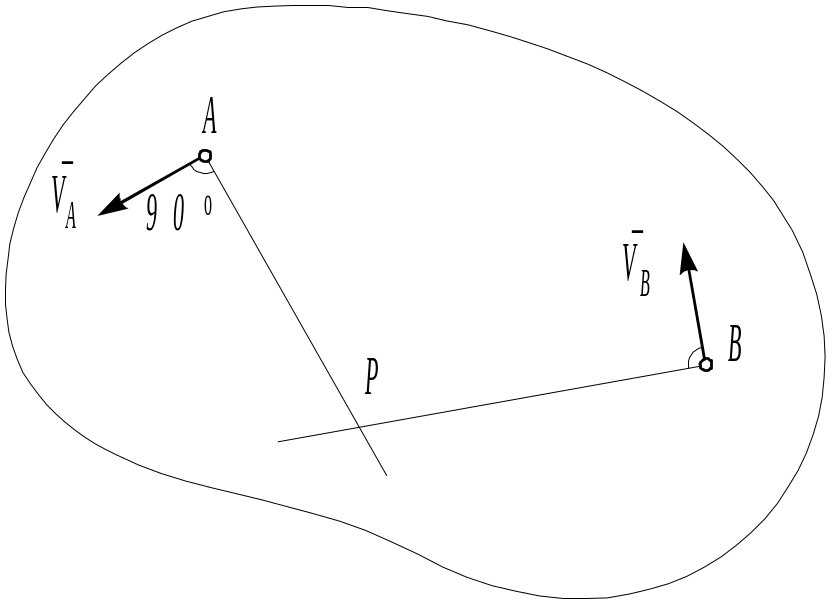
Рис. 4.23

Проведем через точки А и В прямые, перпендикулярные соответственно V_A и V_B. Точка их пересечения P и будет мгновенным центром скоростей.

б) Пусть скорости точек А и В параллельны друг другу и перпендикулярны отрезку АВ (рис. 4.6), причем V_AV_B.

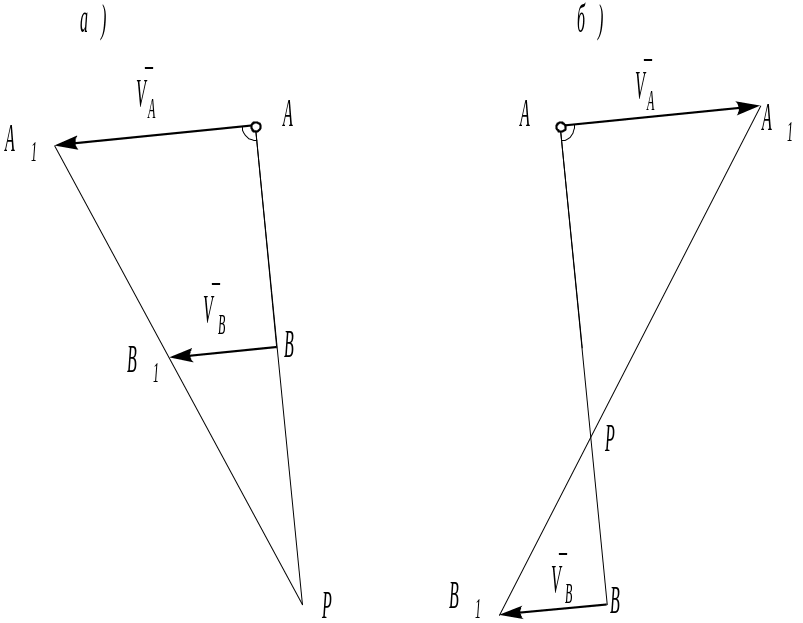
Рис. 4.24

Проведем прямую через концы А₁ и В₁ векторов V_A и V_B. Точка пересечения Р этой прямой с прямой АВ является мгновенным центром скоростей.

в) Пусть скорости точек А и В параллельны друг другу, но не перпендикулярны отрезку АВ (рис. 4.7).

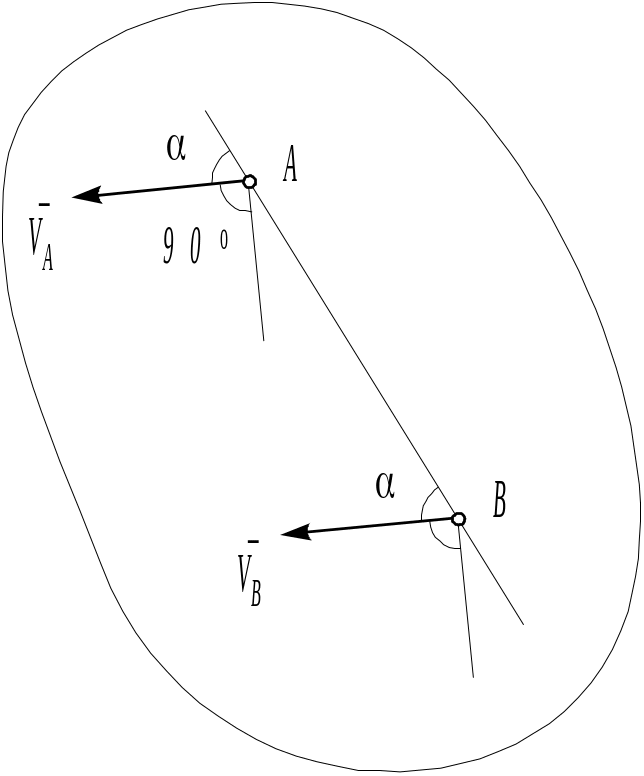
Рис. 4.25

В этом случае прямые линии, неперпендикулярные векторам V_A и V_B, не пересекаются, и мгновенного центра скоростей не существует. Скорости всех точек плоской фигуры в данный момент времени одинаковы. В этом случае скорости точек тела распределены таким образом, как если бы тело совершало в данный момент времени поступательное движение.

г) Пусть диск S катится без скольжения в своей плоскости по некоторой поверхности (рис. 4.8).

Рис. 4.26

В этом случае мгновенный центр скоростей P совпадает с точкой соприкосновения диска S и поверхности. В самом деле, в силу отсутствия скольжения скорость упомянутой точки фигуры S относительно поверхности равна нулю.