- •РАсЧЁт систем водоснабжения и водоотведения на эвм
- •Рецензенты:
- •Введение
- •Глава I. Задачи в системах водоснабжения и водоотведения и математические методы их решения
- •1.1. Методология решения задач с помощью эвм
- •1.2. Задачи, решаемые в отрасли водоснабжения и водоотведения. Их классификация
- •1.3. Задачи, решаемые методами исследования операций
- •1.4. Критерии задач, решаемых в системах водоснабжения и водоотведения
- •1.5. Пример задачи проектирования очистных сооружений
- •1.6. Расчёт параметров по таблицам
- •1.6.1. Линейная интерполяция
- •1.6.2. Интерполяционный полином Ньютона для неравностоящих узлов интерполяции
- •Глава II. Проектирование водоотводящих сетей
- •М оделирование на эвм водоотводящей сети
- •М атематическая модель проектирования хозяйственно-бытовой новой сети
- •2.1. Водоотводящая сеть с точки зрения математики и алгоритм её расчёта
- •Глава III. Проектирование водопроводных сетей с помощью эвм
- •3.1. Подготовка к гидравлическому расчёту
- •3.2. Определение расчётных расходов
- •3.3. Описание программы v_cetu.Exe
- •3.4. Трассировка кольцевой сети. Требования к сети
- •3.5. Потокораспределение
- •3.6. Гидравлический расчет водопроводно-кольцевой сети. Метод Лобачева-Кросса
- •3.7. Метод Ньютона (касательных) решения нелинейных уравнений
- •3.8. Модифицированный метод Ньютона
- •3.9. Метод Ньютона для решения системы нелинейных уравнений
- •3.10. Метод Лобачева-Кросса
- •3.11. Высотное проектирование водопроводной сети. Определение диктующей точки
- •3.12. Определение пьезометрических отметок и построение пьезокарт
- •3.13. Внешняя увязка гидравлической кольцевой сети
- •3.14. Подготовка данных к расчёту на эвм внешней увязки кольцевой сети
- •Глава IV. Применение методов математического моделирования для анализа и расчета систем очистки природных и сточных вод. Принципы и расчёт процессов и аппаратов
- •4.1. Классификация процессов очистки природных и сточных вод
- •4.2. Общие принципы анализа и расчёта процессов и аппаратов очистки природных и сточных вод
- •Уравнения материального баланса
- •Концентрация
- •4.4. Интенсивность процессов и аппаратов
- •4.5. Технологические характеристики аппарата
- •4.6. Аппараты идеального смешения и вытеснения (предельные модели)
- •4.6.1. Аппараты идеального вытеснения
- •4.6.2. Аппарат идеального перемешивания (смешения)
- •4.6.3. Процессы промежуточного типа между идеальным смешением и идеальным вытеснением
- •4.7. Моделирование процесса отстаивания
- •4.8. Моделирование процессов коагуляции и флокуляции
- •4.9. Фильтрование
- •Глава V. Интернет – источник получения информации
- •Основные принципы, лежащие в основе работы сети Интернет
- •5.2. Технология поиска информации
- •Составляющие решения поисковой задачи
- •Цель поиска.
- •Средства поиска.
- •Методы.
- •Компьютерные технологии в учебном процессе
- •Задачи для практических занятий
- •Задания для лабораторных занятий
- •Тестовые вопросы по дисциплине «Расчёт систем ВиВ на эвм»
- •Тематика рефератов
- •Заключение
- •Основные приёмы редактора электронных таблиц Excel
- •Оглавление
- •Учебное издание Ирина Владимировна Журавлева
- •3 94006 Воронеж, ул. 20-летия Октября, 84
2.1. Водоотводящая сеть с точки зрения математики и алгоритм её расчёта
С математической точки зрения водоотводящая сеть представляет собой связный граф без циклов (дерево). Он имеет множество вершин – М и рёбер – N, соединяющих вершины графа (zi1, zi2), zi1, zi2 М, i1i2. N =М-1.
Ребро li1=(zi1, zi2) – обозначение. Читается: ребро li1 исходит из вершины zi1 и ведёт к вершине zi2. Так как водоотводящая сеть предусматривается безнапорной и вода в ней движется только под собственным весом, то исходную вершину (zi1) справедливо назвать верхней, а вершину zi2 – нижней (по ходу движения воды).
Последовательность ребер li1, li2, li…, lik назовём путём длины k, если каждое ребро lij ведёт в вершину, из которой исходит ребро lij+1 j=1, …, k-1.
Очевидно, что путь длиной k можно представить в виде последовательности рёбер, соединяющих вершины zi1,…, zik+1. Пример приведён на рис. 10.
Рёбра l1=(1, 2); l2=(2, 3); l3=(3, 4); l4=(4, 5); l5=(5, 6); l6=(6, 7); l7=(7, 8); l8=(8, 9); l9=(9, 10); l10(10, 11); l11=(11, 12) составляют путь длиной k=1...12 от вершины 1 до корневой вершины 12. Рёбра l12=(14, 15) и l13=(15, 6) составляют путь длиной k1 = 14...6 от вершины 14 до вершины 6.

Рис. 10. Пример дерева водоотводящей сети
Цепью наибольшей длины будет та цепь, которая содержит наибольшее количество рёбер. Для нашего примера это путь k.
Начальные вершины цепи называются висячими. С этих вершин начинаются пути.
Будем считать, что каждому ребру графа lj поставлен в соответствие некоторый расход Qj0 j=1,…, m – пропускная способность ребра (дуги) lj.
Определяют этот расход для каждого квартала в зависимости от модуля стока:
![]() ,
л/(сга), (2.1)
,
л/(сга), (2.1)
где p – плотность населения, чел./га;
qб – норма водоотведения бытовых вод л/(сут.чел.).
и площади квартала (Fi), с которого поступает сточная жидкость в вершину рассматриваемого ребра
Qj=Fiq0, л/с. (2.2)
Основной задачей теории потоков в сетях является задача построения максимального потока q. Поэтому трассировку сети и нумерацию расчётных точек выполняют сначала с главного или бассейнового коллекторов, а затем - уличной сети по принципу дерева. Начинают нумерацию по цепи наибольшей длины от висячего колодца до прикорневой точки (корневой вершины), в которую самотёком приходят сточные воды с бассейна. Далее нумеруют цепи, соответствующие толстым ветвям дерева, и последними нумеруют участки, соответствующие самым тоненьким веточкам.
Различают несколько видов расходов: попутный, транзитный, средний, максимальный и сосредоточенный.
Попутный расход образуется с прилегающего к ребру квартала - qпоп.
Транзитный расход – это расход, проходящий от нижней вершины первого ребра до корневой вершины (qтранз.). На рёбрах с висячими вершинами транзитных расходов не бывает.
Средний расход складывается из попутного и транзитного расходов участка. В качестве транзитных расходов принимаются средние расходы с вышележащих рёбер. Например, (см. рис. 10) для ребра l6=(6, 7) в качестве транзитного расхода следует принимать сумму средних расходов рёбер l5=(5, 6) и l13=(15, 6). По каждому бассейну выполняют промежуточную проверку. В корневой вершине средний расход должен совпадать со средним расходом по бассейну, с которого собирается сточная вода в эту вершину самотёком.
Максимальный секундный расход на любом участке (ребре) сети получается умножением среднего расхода участка на коэффициент общей неравномерности [14, с. 34, формула (1.10)].
В качестве сосредоточенных расходов следует принимать расходы от насосных станций, перебрасывающих сточную воду через водораздел и присоединяющихся к коллектору; а также расходы промышленных предприятий.
В качестве расчётного расхода промышленного предприятия следует принимать суммарный расход максимальных секундных расходов бытовых и производственных сточных вод из [31, табл. 4].
В качестве расчётного расхода от насосных станций следует принимать при равномерной работе станции средний секундный расход, а при ступенчатой работе – максимальный секундный расход, соответствующий максимальной ступени.
Рассмотрим пример трассы и сбор расходов с участков сети с учётом рельефа местности.
Сначала пронумеровали наиболее длинную цепь (рис. 11) 1 - 8, затем все остальные подсоединения к этой цепи (9 – 4; 11 - 6; 14 – 6; 16 – 7).

Рис. 11. Расчётная схема водоотводящей сети
Собирать расходы следует сначала с самых тонких ветвей, затем с тех, что «потолще» и только потом ‑ по стволу к прикорневому колодцу.
Попутные расходы собираются с прилегающего к данному расчётному участку квартала (или нескольких кварталов или их частей как в примере на участке 5 – 6 с кварталов 8а и 9а). Расходы с кварталов определяются раньше по плотности населения и норме водоотведения [31, с. 7 – 9]. Транзитные расходы при написании программы для ЭВМ можно определять автоматически в цикле, сравнивая цифру первого колодца расчётного участка с последней цифрой всех предыдущих участков [13]. При этом необходимо выполнить обязательные условия: строго начинать сбор расходов с самых тоненьких веточек, постепенно переходя к стволу; строго соблюдать направление течения воды по участку, первая цифра расчётного участка должна обозначать начальный колодец (исток), а вторая – конечный (куда втекает сток с участка). При работе в среде Excel у студента всегда перед глазами план города, поэтому себя можно проконтролировать визуально и по предложенному для ЭВМ алгоритму (прил. 2), чтобы не упустить боковые притоки. Можно сделать проверку расчётов, сравнивая расход в прикорневой точке с расходом от всего бассейна. Сразу будет видно правильно ли разбит город на бассейны канализования и правильно ли собраны расходы по участкам. Если условие не выполнено, то надо искать ошибку, анализируя принадлежность участков к тому или иному бассейну, и проверять попутные и путевые расходы в табл. 1. В качестве транзитного принимается средний расход qmid.s с предыдущего участка (или расходы, если в колодец вливается сток с нескольких участков). Например, на участке 4 – 5 транзитными будут расходы с участков 3 – 4, 10 – 4. Транзитных расходов не будет на висячих участках. Средний расход на расчётном участке принимается в общем виде как сумма попутного и транзитного расходов. Далее определяется методом интерполяции коэффициент общей неравномерности как функция от среднего расхода по участку Кgen.max=f(qmid.s) по [31, табл. 9]. Максимальный секундный расход qmax.s. получается перемножением среднего секундного расхода и коэффициента общей неравномерности.
Таблица 3
Определение расчетных расходов на участках водоотводящей сети
Номера расчётных участков |
Средние расходы |
Кgen.max |
Максимальный секундный расход, qmax.s., л/с |
Сосредоточенный расход qсоср, л/с |
Суммарный расчётный расход, qcit, л/с |
|||||
попутные |
транзитные |
qmid.s, л/с |
||||||||
номера кварталов |
qпоп., л/с |
транзитные участки |
qтр., л/с |
мест-ный |
транзитный |
|||||
9-10 |
5 |
1 |
- |
|
1 |
2,5 |
2,5 |
|
|
2,5 |
10-4 |
4 |
1,2 |
9-10 |
1 |
2,2 |
2,5 |
5,5 |
|
|
5,5 |
11-12 |
6 |
0,6 |
- |
|
0,6 |
2,5 |
1,5 |
|
|
1,5 |
12-13 |
7 |
1,0 |
11-12 |
0,6 |
1,6 |
2,5 |
4,0 |
|
|
4,0 |
13-6 |
12б |
0,54 |
12-13 |
1,6 |
2,14 |
2,5 |
5,35 |
|
|
5,35 |
14-15 |
10 |
0,98 |
- |
|
0,98 |
2,5 |
2,45 |
|
|
2,45 |
15-6 |
9б |
0,58 |
14-15 |
0,98 |
1,56 |
2,5 |
3,9 |
|
|
3,9 |
16-17 |
11 |
1,43 |
- |
|
1,43 |
2,5 |
3,575 |
|
|
3,575 |
17-7 |
12б |
0,54 |
16-17 |
1,43 |
1,97 |
2,5 |
4,925 |
|
|
4,925 |
1-2 |
1 |
1,1 |
- |
|
1,1 |
2,5 |
2,75 |
|
|
2,75 |
2-3 |
2 |
0,9 |
1-2 |
1,1 |
2,0 |
2,5 |
5,0 |
|
|
5,0 |
3-4 |
3 |
0,9 |
2-3 |
2,0 |
2,9 |
2,5 |
7,25 |
|
|
7,25 |
4-5 |
- |
|
3-4, 10-4 |
2,9 2,2 |
5,1 |
2,492 |
12,7092 |
|
|
12,71 |
5-6 |
8а, 9а |
1,12 |
4-5 |
5,1 |
6,22 |
2,402 |
14,943 |
п.п. 32,5 |
|
47,443 |
6-7 |
12а |
0,54 |
5-6, 13-6, 15-6 |
6,22 2,14 1,56 |
9,92 |
2,106 |
20,895 |
|
п.п. 32,5 |
53,395 |
7-8 |
- |
- |
6-7, 17-7 |
9,92 1,97 |
11,89 |
2,062 |
24,52 |
|
п.п. 32,5 |
57,02 |
В качестве сосредоточенных расходов принимаются расходы промышленных предприятий или районных канализационных насосных станций (если таковые есть). Сосредоточенные расходы принимаются как местные для расчётного участка, когда они поступают впервые в сеть в первый колодец расчётного участка (например, для участка 5 – 6 сосредоточенный расход от промышленного предприятия учитывается как местный qсоср.(5-6)=32,5, а для участков 6 – 7 и 7 – 8 сосредоточенный расход от промышленного предприятия учитывается как транзитный). Расчётный расход на i-ом участке сети (гр. 11, табл. 3) определяется суммированием максимального секундного и
сосредоточенного расходов: qcit(i) = [qпоп.(i) + qтр.(i)]* Кgen.max(i) + qсоср.(i), л/с. (2.3)
Далее определяются начальные заглубления висячих колодцев водоотводящей сети (расчёт сводится в табл. 4) по следующему алгоритму:
назначается минимальный диаметр внутриквартальной сети dв/к, м;
определяется расстояние от первого колодца до контрольного колодца внутриквартальной сети L, м, по генплану города;
определяется расстояние от контрольного колодца внутриквартальной сети до рассматриваемого уличного колодца l/2, м;
определяются абсолютные отметки земли в начале внутриквартальной сети (z2) и около уличного колодца (z1) по генплану города;
определяется начальное заглубление лотка трубы в первом колодце квартала (hmin). Допускается принимать минимальную глубину заложения на 0,3 м выше глубины промерзания грунта (для труб d< 500 мм):
hmin = (hпр. – 0,3) (0,7+d), м, (2.4)
где hпр. – глубина промерзания грунта, м, (определяется по карте нормативных глубин промерзания [14, рис. 4.4]; d - диаметр трубы уличной сети, м;
оценивается уклон поверхности земли от начального внутриквартального колодца до уличного колодца (iзем.) и сравнивается с нормативным минимальным уклоном для трубопровода внутриквартальной сети (табл. 5).
Если iзем.>
![]() ,
то imin
= (z2-
z1
-d)/
(L
+ l/2). (2.5)
,
то imin
= (z2-
z1
-d)/
(L
+ l/2). (2.5)
Если iзем. , то imin = ; (2.6)
определяется начальное заглубление лотка уличного колодца в зависимости от выбранного уклона.
Если iзем.> , то Н= hmin. (2.7)
Если imin = , то Н= hmin+ imin*(L+ l/2)+ d – (z2- z1). (2.8)
Таблица 4
Начальные заглубления висячих колодцев водоотводящей сети
Номера колодцев уличной сети |
Диаметр внутриквартальной сети |
Длина внутриквартальной сети по кварталу |
Длины сети от контрольного колодца до уличного |
Абсолютная отметка земли в начале внутриквартальной сети |
Абсолютная отметка земли около уличного колодца |
Начальное заглубление лотка трубы в первом колодце квартала, м |
Уклон поверхности земли от начального до уличного колодцев |
Уклон внутриквартальной трубы, |
Начальное заглубление лотка уличного колодца |
|
dв/к, м |
L, м |
l/2, м |
z2, м |
z1, м |
hmin |
iзем. |
imin |
Н, м |
1 |
0,15 |
45 |
20 |
85,34 |
83,87 |
1,0 |
0,0226 |
0,0218 |
1,0 |
9 |
0,15 |
40 |
20 |
85,44 |
83,83 |
1,0 |
0,0268 |
0,026 |
1,0 |
11 |
0,15 |
20 |
20 |
81,17 |
79,90 |
1,0 |
0,03175 |
0,0305 |
1,0 |
14 |
0,15 |
50 |
20 |
79,17 |
78,00 |
1,0 |
0,0167 |
0,016 |
1,0 |
16 |
0,15 |
60 |
20 |
77,44 |
75,00 |
1,0 |
0,0305 |
0,03 |
1,0 |
Рассмотренный алгоритм использован в программе ceti_k2 (прил. 2).
Таблица 5
Ограничения, принимаемые на основании нормативных документов
d, мм |
h/dmax |
min, м/с |
|
d, мм |
h/dmax |
min, м/с |
|
150 200 250 |
0,6 |
0,7 |
0,008 0,007 1/d |
300…400 450…500 600…800 900 1000…св. 1500 |
0,75
|
0,8 0,9 1,0 |
1/d |
1,15 |
|||||||
0,8 |
Нормативные требования в значительной степени и определяют заглубления уличных сетей и коллекторов особенно в тех случаях, когда рельеф местности на начальных участках сети имеет обратный уклон (рис. 12, а), является горизонтальным (рис. 12, б) либо меньше или равен минимальному уклону труб (рис.12, в, г). В этих случаях диаметр труб подбирают из условия пропуска расчётного расхода сточных вод при уклоне, обеспечивающем допустимые наполнения и скорости не ниже минимально допустимых. Если при выполнении соответствующих требований не удаётся избежать значительных заглублений сети, то для уменьшения заглублений труб целесообразно использовать расчётные участки со станциями перекачки (рис. 12, е), принимая на них минимальные уклоны укладки труб.

Рис. 12. Возможные случаи уклонов поверхности земли
на расчётных участках
Выбор уклона трубы выполняется в зависимости от уклона земли по следующим формулам
imр.= iзем.=(zз.н. – zз.к.)/L; (2.9)
imр.= . (2.10)
Если уклон поверхности земли больше минимального нормативного (рис. 12, д) и заглубление сети в начальном колодце на расчётном участке больше минимального, то целесообразно принять уклон трубопровода по формуле (2.11), чтобы в конец участка получить минимальное заложение лотка:
iзем. > imр. > . (2.11)
Таблица 6
Значения наименьших уклонов и диаметров в зависимости от расчётных расходов
Расход q, л/с |
Скорость , м/с |
Уклон i |
Наполнение h/d |
Диаметр труб ПНД d, мм |
1,5–4,4 2,2–5,9 1,3–8,5 3 – 12 4,7–16,3 5,6–19,6 6,1–23,6 7,7 – 26,7 10,4–36,21 19,2–54,7 26–63 28,9–77,3 79,6–99 94,6–133 94,1–161 |
0,78–0,83 0,83–0,85 0,7 –0,77 0,76–0,81 0,85–0,88 0,83–0,86 0,77–0,82 0,73–0,75 0,79–0,81 0,84–0,89 0,83–0,84 0,82–0,85 0,9–0,91 0,91–0,92 0,9–0,91 |
0,01 0,009 0,01 0,006 0,006 0,005 0,004 0,004 0,003 0,0025 0,002 0,0015 0,0014 0,0013 0,0012 |
0,3 0,3 0,2 0,3 0,3 0,2 0,3 0,3 0,3 0,4 0,4 0,5 0,6 0,6–0,7 0,5 |
110 125 140 160 180 200 225 250 280 315 355 400 450 500 560 |
При слишком крутом рельефе местности, даже при прокладке труб с максимальными уклонами, при которых скорость движения жидкости достигает максимально допустимых значений, глубина заложения сети все же может оказаться меньше допустимых значений. Для увеличения заглубления можно использовать приемы укладки труб (рис. 13).
Каждый участок сети следует рассчитывать исходя из схемы, представленной на рис. 14.
Расчёт числа
Рейнольдса: ![]() ,
где =f(t,K0), (2.12)
,
где =f(t,K0), (2.12)
где R – гидравлический радиус, м, R=q/(2d); - скорость, м/с; - коэффициент кинематической вязкости м2/с.
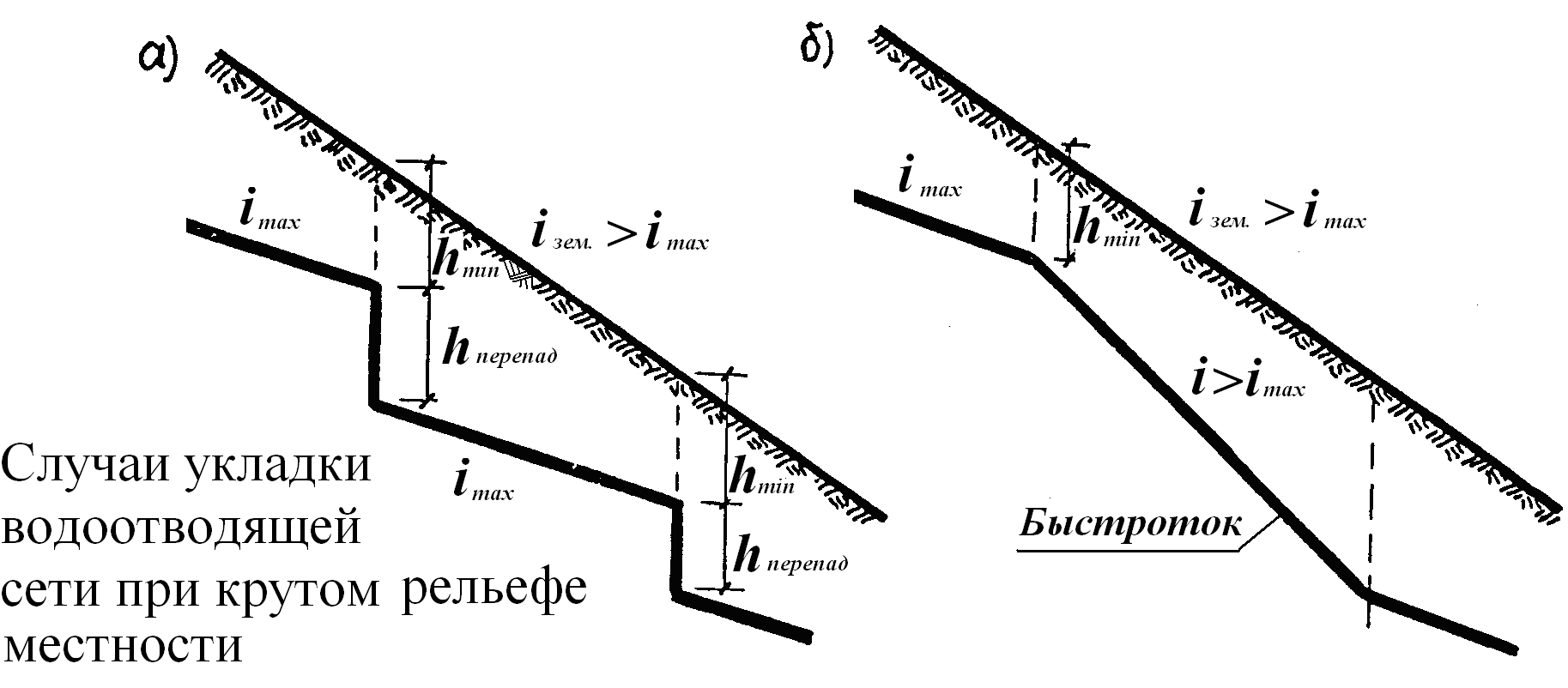
Рис.13. Укладка трубопроводов:
а) с перепадами; б) с быстротоком
В зависимости от величины Re определяется коэффициент гидравлического сопротивления .
При Re100000 =0,3164/ Re0,25 – по формуле Блазиуса. (2.13)

Р
zл.н.=zз.н.-
hн; (4.3)
zл.к.
=
zл.н.-h; (4.4)
hк.=zз.к.
–zл.к.; (4.5)
zв.н.=
zл.н.+h; (4.6)
zв.к.=
zл.к+h=
zв.н.
-h
(4.7)
При Re>100000 коэффициент гидравлического сопротивления определяется по формуле
 . (2.14)
. (2.14)
Уклон определяется
по формуле ![]() .
(2.15)
.
(2.15)
Потеря по длине участка определяется по формуле Н=iL. (2.16)
В начальных участках отметки определяются по формулам
zл.н.=zз.н.- hн; (2.17)
zл.к. = zл.н.- Н; (2.18)
zв.н.= zл.н.+h; (2.19)
zв.к.= zл.к+h= zв.н. -Н.; (2.20)
hк.=zз.к. –zл.к.. (2.21)
На следующем участке определяются скорость, уклон, наполнение, потеря по длине и в зависимости от диаметров, наполнений и скоростей на расчётном и предыдущем участках рассматривают различные варианты сопряжения трубопроводов (рис. 15).
1а) |
|
|
|
|
|
Рис. 15. Способы соединения труб в колодцах (к табл. 7)
Расчётные формулы сопряжения лотков в колодцах сведены в табл. 7. Ими успешно можно пользоваться при гидравлическом расчёте сети в редакторе Microsoft Office Excel, форма таблицы соответствует [31, табл. 12].
Если глубина заложения сети превышает 6 м, то устанавливают насосную станцию. И на следующем участке принимают начальное заглубление
Н = (hпр. – 0,3) (0,7+d), м. (2.22)
Остальные расчёты выполняются как на начальных участках.
Таблица 7
Варианты сопряжения трубопроводов в колодце к рис. 15
Сравнение параметров на предыдущем (первом) и расчётном (втором) участках |
Метод соединения трубопроводов |
Расчётные формулы |
а) h1<h2 и 21
б) 21
в) h1>h2, i1≤i2 |
по воде |
zв.н.(2)= zв.к.(1) zл.н(2)= zв.н.(2) –h2 zл.к.(2) = zл.н.(2)-h2; zв.к.(2)= zв.н.(2) -h2= zл.к.(2)+h2 hн(2).=zз.н.(2) –zл.н(2) hк(2).=zз.к.(2) –zл.к(2) |
zв.н.(2)= zв.к.(1) –0,15 остальные формулы те же |
||
по лоткам |
hн(2).= hк(1) zл.н(2)= zл.к.(1); zл.к.(2) = zл.н.(2)-h; hк(2).=zз.к(2). –zл.к(2).; zв.н.(2)= zл.н.(2)+h2; zв.к(2).= zл.к(2)+h2= zв.н.(2) -h2 |
|
а) h1≤h2 и (d2-d1) ≤(h2-h1) и 21 б) 21 и (d2-d1)> (h2-h1+{0,1-0,2})
в) h1<h2 и (d2-d1) >(h2-h1)
г) h1>h2, i1≤i2 |
по воде
|
алгоритм п.1,а) алгоритм п.1.б) |
по шелыгам |
hн(2).= hк(1)+ (d2-d1), м zл.н(2)= zз.н.(2)- hн(2) zл.к.(2) = zл.н.(2)-h; hк(2).=zз.к(2). –zл.к(2).; zв.н.(2)= zл.н.(2)+h2; zв.к(2).= zл.к(2)+h2= zв.н.(2) -h2 |
|
по лоткам |
алгоритм п.1, в) |
|
3. d1>d2 h1>h2, i1≤i2 |
по лоткам |
алгоритм п.1, в) |
Затем строится профиль укладки трубопроводов (рис. 16).
На профиле показывается геологический разрез и боковые присоединения в расчётных колодцах. Наносятся все основные расчётные параметры: расход и скорость сточных вод на участке, диаметр, уклон и наполнение трубы, отмечается уровень грунтовых вод и заглубление лотка трубы относительно отметки земли.

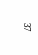
Р ис.16.
Продольный профиль водоотводящей сети
к проектному заданию
ис.16.
Продольный профиль водоотводящей сети
к проектному заданию