§ 2. Дифференциальные уравнения высших
ПОРЯДКОВ
2.1. Дифференциальные уравнения второго
ПОРЯДКА
Уравнение
,
(2.1)
связывающее между собой независимую
переменную, неизвестную функцию
,
а также ее первые две производные
и
,
называется дифференциальным уравнением
второго порядка.
Если уравнение можно записать в виде
,
(2.2)
то говорят, что оно разрешено относительно второй производной.
Задача отыскания решения уравнения (2.2), удовлетворяю-
щего заданным начальным условиям
,
где
-
некоторые числа называется задачей
Коши.
Решением уравнения (2.2) называется
всякая функция
,
которая при подстановке вместе с
и
в это
уравнение обращает его в тождество. График функции в этом случае называется интегральной кривой.
Общим решением уравнения (2.2)
называется функция
,
зависящая от двух произвольных постоянных
и
и такая, что:
она является решением этого уравнения при любых конкретных значениях и
при любых допустимых начальных условиях
(2.3)
можно подобрать такие значения постоянных
и
,
что функция
будет удовлетворять этим начальным
условиям.
Любая функция , получающаяся из общего решения уравнения (2.2) при конкретных значениях постоянных и , называется частным решением этого уравнения.
Для дифференциального уравнения второго порядка имеет место теорема существования и единственности решения, аналогичная соответствующей теореме для уравнения первого порядка.
Теорема. Если функция
и ее частные производные
и
непрерывны в некоторой области
,
содержащей точку с координатами
,
то существует и притом единственное
решение
уравнения (2.2), удовлетворяющее начальным
условиям
.
Общий интеграл
или общее решение
уравнения (2.2) представляет собой семейство
кривых, зависящих от двух произвольных постоянных
и
.
Задача Коши в таком случае состоит в
определении интегральной кривой
,
проходящей через данную точку
и имеющей данный угловой коэффициент
касательной, т.е.
2.2. Понижение порядка дифференциальных
УРАВНЕНИЙ
В некоторых частных случаях удается понизить порядок дифференциального уравнения второго порядка. Зачастую оно в итоге приводится к дифференциальному уравнению первого порядка одного из изученных ранее типов. Рассмотрим наиболее типичные случаи.
Уравнения вида
.
Интегрированием обеих частей уравнения оно приводится к уравнению первого порядка
Повторно интегрируя полученное равенство, находим общее решение исходного уравнения:
Дифференциальные уравнения
,
явно не содержащие искомой функции
Такие уравнения допускают понижение
порядка подстановкой
,
т.е. данное уравнение равносильно системе
дифференциальных уравнений первого
порядка
Дифференциальные уравнения
,
явно не содержащие независимой переменной
.
Уравнения такого вида допускают
понижение порядка подстановкой
т.к. формальное отсутствие аргумента
позволяет считать неизвестную функцию
функцией аргумента
,
тогда
.
Таким образом, уравнение равносильно системе
Интегрирование дифференциальных уравнений порядка выше второго.
Приемы, описанные выше, можно распространить на уравнения более высокого порядка.
Общее решение простейшего
дифференциального уравнения
-го
порядка
находится
-кратным
интегрированием функции
и содержит
произвольных
постоянных.
Дифференциальное уравнение вида
не содержащее в явном виде искомой
функции
,
допускает понижение порядка подстановкой
Другими словами, данное уравнение
равносильно системе
Дифференциальное уравнение вида
,
не содержащее явно аргумент
,
допускает понижение порядка на единицу
подстановкой
.
При этом (по правилу дифференцирования
сложной функции):
и т.д.
Задача 2.1. Найти частное решение данного дифференциального уравнения, удовлетворяющее заданным начальным условиям:
Решение. Находим общее решение.
Интегрируя по частям, находим
=
Повторное интегрирование по частям приводит к общему решению:
С учетом заданных начальных условий,
получаем систему уравнений для
определения неизвестных констант
и
Найденные значения постоянных подставляем в общее решение. Получаем искомое частное решение
Задача 2.2. Решить дифференциальное
уравнение
Найти частное решение, если
.
Решение. Данное дифференциальное
уравнение второго порядка не содержит
явно искомую функцию
,
т.е. имеет вид
.
Положим
,
тогда
.
Получаем дифференциальное уравнение
первого порядка
- линейное относительно неизвестной
функции
.
Общее решение этого уравнения найдем
подстановкой
,
.
Получаем:
тогда
Из первого уравнения находим
,
т.е.
Подставляя
во второе уравнение, получим
,
откуда
Следовательно,
,
т.е.
.
Интегрируя это равенство, найдем общее
решение исходного уравнения
.
Подставляя в два последних равенства начальные условия , получаем
Найденные значения
и
подставляем в общее решение. Отсюда
искомое частное решение
Задача 2.3. Найти общее решение дифференциального
уравнения
.
Найти частное решение, удовлетво-
ряющее начальным условиям
Решение. Данное дифференциальное
уравнение не содержит в явном виде
аргумента
,
т.е. имеет вид
.
Примем в качестве независимой переменной
и выполним замену
Тогда
,
а исходное уравнение принимает вид:
Если
,
то
,
и
После сокращения на
решим дифференциальное уравнение
первого порядка
.
Это уравнение с разделяющимися
переменными. Разделяя переменные
и интегрируя, получим
,
откуда
(заметим, что найденное ранее решение
содержится в полученном выражении при
).
Заменим
на
и решим уравнение
,
которое также является уравнением с
разделяющимися переменными:
,
или
Получили общее решение исходного
уравнения с неявном виде. Из начальных
условий имеем
или
,
а из равенства
,
находим
.
Подставляя полученные значения констант
в общее решение, которое запишем в виде
,
находим требуемое частное решение
.
Задача 2.4. Найти общее решение
дифференциального уравнения третьего
порядка
Решение. Это простейшее дифференциальное уравнение решается трехкратным интегрированием правой части. Сначала понизим степень косинуса:
После первого интегрирования получаем
после второго
а после третьего – общее решение
Замечание. Произведение произвольных
постоянных на конкретные числа также
можно считать произвольными постоянными.
Например, в общем решении можно писать
вместо
Задача 2.5. Решить дифференциальное
уравнение четвертого порядка
Решение. Это уравнение имеет вид
,
поэтому его порядок можно понизить на
три единицы при помощи замены
Приходим к уравнению
.
Рассмотрим два случая:
если , т.е.
,
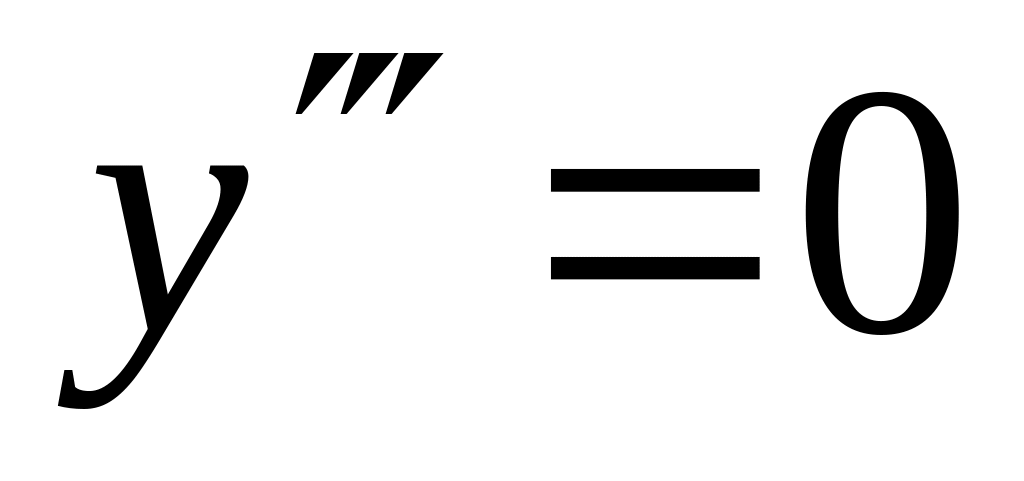то
-
не общее решение;если , то
.
Отсюда получаем
или
Последовательные
интегрирования дают
к которому присоединим полученное ранее
не общее решение
Задача 2.6. Найти частное решение
дифференциального уравнения
удовлетворяющее начальным условиям
Решение. Данное уравнение имеет вид
,
т.е. не содержит явно
и
Поэтому положим
Получаем линейное относительно
неизвестной функции
уравнение
Его общее решение имеет вид
Остается
решить простейшее дифференциальное
уравнение
Подставив из начальных условий
находим
Интегрируя получающееся равенство
,
имеем
Снова подставляя начальные условия
находим
.
Значит,
Отсюда
учитывая, что
,
т.е.
получим
и следовательно,
.
Найти общие решения данных дифференциальных уравнений, а там, где указаны начальные условия, найти соответствующее частное решение:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
Ответы: 1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
и
20.
21.
22.
.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальные и интегральные исчисления / Н.С. Пискунов.- М.: Наука, 2001.Т.2.- 576 с.
2. Агафонов С.А. Дифференциальные уравнения / С.А. Ага-
фонов, А.Д. Герман, Т.В. Муратова. - М.: Изд-во МГТУ им.
Н.Э. Баумана, 2000.-348 с.
3. Данко П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: «Оникс 21
век» «Мир и образование», 2003. Ч. 2.
4. Зимина О.В. Высшая математика / О.В. Зимина, А.И. Кириллов, Т.А. Сальникова.- М.: Физико-математическая литература, 2001.-368 с.
5. Ефимов А.В. Сборник задач по математике для втузов / А.В. Ефимов, Б.П. Демидович; под ред. А.В. Ефимова. - М.: Наука,1986. –Ч.2.-368 с.
6. Лунгу К.Н. Сборник задач по высшей математике. 2 курс/К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А. Шевченко; под ред. С.Н. Федина. - М.: Айрис-пресс, 2005.-592 с.
7. Рябушко А.П. Индивидуальные задания по высшей математике: Комплексные числа. Неопределенные и определенные интегралы. Функции нескольких переменных. Обыкновенные дифференциальные уравнения / А. П. Рябушко и др.; под общ. ред. А. П. Рябушко.- 3-е изд.- Минск.: Выш. шк., 2007.-396 с.