Работа. Энергия системы зарядов

Задача 1.17. Две частицы, обладающие массами m₁ и m₂ и зарядами +q₁ и +q₂, движутся навстречу друг другу, имея вдалеке относительную скорость _отн. На какое наименьшее расстояние сблизятся частицы.

Дано: m1 m2 q1 q2

rmin – ?

Решение

Рассмотрим движение частиц в какой-либо «лабораторной» системе отсчета, например, связанной с Землей. Полагая систему двух заряженных частиц изолированной, воспользуемся законом сохранения энергии: где W – полная энергия частиц. Последние обладают в каждый момент времени кинетической энергией, а также потенциальной энергией кулоновского взаимодействия.

Когда частицы находятся вдалеке друг друга, то их потенциальной энергией можно пренебречь.

Тогда полная энергия системы равна:

,

(1)

где и – скорости частиц в выбранной системе отсчета.

Так как векторы и направлены противоположно, то значения и связаны с заданной относительной скоростью _отн соотношением:

или ,

(2)

При сближении частиц потенциальная энергия их кулоновского взаимодействия (отталкивания), будучи величиной положительной, начнет увеличиваться. Следовательно, суммарная кинетическая энергия частиц станет уменьшаться. Частицы не могут как угодно близко подойти друг к другу, иначе их потенциальная энергия оказалась бы больше полной энергии W₁, противоречит условию .

При наибольшем сближении частиц, когда расстояние между ними равно r_min полная энергия равна:

,

(3)

где W_min – кинетическая энергия системы.

Чтобы найти W_min, учтем, что в момент наибольшего сближения частиц их скорости будут одинаковыми: . Действительно, когда скорости частиц неодинаковые, расстояние между ними растет или уменьшается и, следовательно, не является минимальным.

Применив к системе закон сохранения импульса, запишем:

,

(4)

где - импульс системы удаленных частиц, - импульс системы при наибольшем сближении. При этом вектор предположительно выбран совпадающим по направлению с вектором (очевидно, при подсчете кинетической энергии направление скорости несущественно).

Из уравнения (4) имеем:

,

тогда для величины W_min получим:

,

(5)

Подставив (5)в (3) и приравняв правые части (1) и (3) на основе закона сохранения энергии, а также учитывая (2), найдем:

.

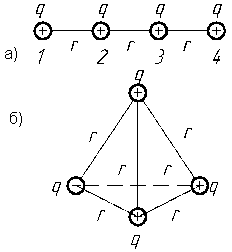
Задача 1.18. Четыре одинаковых точечных заряда q расположены на одной прямой, на расстоянии r друг от друга. Какую работу надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.

Дано: q r ε =1

А – ?

Р ешение

Р

Рис. 1.15

абота по переносу зарядов равна разности энергий системы: зарядов W₂, расположенных в вершинах тетраэдра (рис. 1.15б) и энергии системы W₁, расположенных на одной прямой (рис. 1.15а):

(1)

Энергия системы N точечных зарядов определяется формулой:

,

здесь q – заряд в некоторой точке, – потенциал поля в этой же точке, созданного зарядами системы.

Запишем эту формулу применительно к системе четырех зарядов, расположенных на одной прямой:

,

(2)

здесь , , , – потенциалы поля, созданного в точках 1, 2, 3, 4 остальными зарядами, не считая того заряда, который находится в данной точке.

Потенциал поля в точке 1, созданного зарядами в точках 2, 3, 4 равен:

,

(3)

В силу симметрии . (4)

Потенциал в точке 2, созданного зарядами в точках 1, 3, 4 равен:

,

(5)

В силу симметрии . (6)

Подставим (3)-(6) в (2):

,

(7)

Теперь определим энергию системы зарядов , расположенных в вершинах тетраэдра. Очевидно, что энергия заряда в одной вершине равна:

,

где – потенциал поля, созданного в этой вершине каждым из остальных трех зарядов.

В силу симметрии вся энергия этой системы четырех зарядов будет в четыре раза больше:

, где .

Поэтому (8)

Поставим (7) и (8) в (1):

Ответ: .

Задача 1.19. В однородное электростатическое поле напряжённостью =700 перпендикулярно полю поместили стеклянную пластину толщиной =1,5 , площадью =200 и относительной диэлектрической проницаемостью =7. Определить: 1) поверхностную плотность связанных зарядов на стекле; 2) энергию электростатического поля, сосредоточенную в пластине.

Дано: =700 =7 =1,5мм=1,5 =200 =2

-? -?

Решение

Зная и , выражаем напряжённость поля в стекле и электрическое смещение

, .

Тогда поверхностная плотность связанных зарядов равна:

(1)

Энергию электростатического поля, сосредоточенную в пластине, можно найти через объемную плотность энергии электрического поля и объём

(2)

Подставив числовые значения в выражения (1) и (2), получим:

(пДж)

Ответ: ; пДж.

Задача 1.20. Пространство между пластинами плоского конденсатора заполненного стеклом . Когда конденсатор присоединили к источнику напряжения, давление пластин на стекло оказалось равным 1Па. Определить: 1) поверхностную плотность зарядов на пластинах конденсатора; 2)электрическое смещение; 3) напряжённость электростатического поля в стекле; 4) поверхностную плотность связанных зарядов на стекле; 5) объёмную плотность энергии электростатического поля в стекле.

Дано: 7 1Па

w-?

Решение

Давление пластин конденсатора на стекло равно

, (1)

где (2)

Подставив выражение (2) в (1), получим

(3)

Электрическое смещение равно

и , (4)

следовательно, . (5)

Поверхностная плотность связанных зарядов на стекле равна поляризованности

(6)

Объёмная плотность энергии электрического поля в стекле равна

(7)

Подставив числовые значения, получим:

=11,1 ( )

( )

( )

( )

Ответ: , , , , .

Задача 1.21. Две концентрические сферы радиусами заряжены соответственно одинаковыми зарядами . Определить энергию электростатического поля, заключённого между этими сферами.

Дано:

Решение

Р

Рис. 1.16

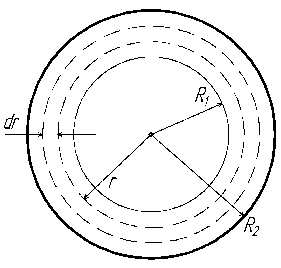
азобьём про­странство между сфе­рами на отдельные концентрические сферы бесконечно ма­лой толщины с внутренним радиусом и внешним (рис. 1.16).

Воспользуемся формулой для определения объёмной плотности энергии электростатического поля

, (1)

где , тогда энергия электростатического поля, заключённого между сферами, может быть определена путём интегрирования

, . (2)

Используя выражения (1) и (2), получим

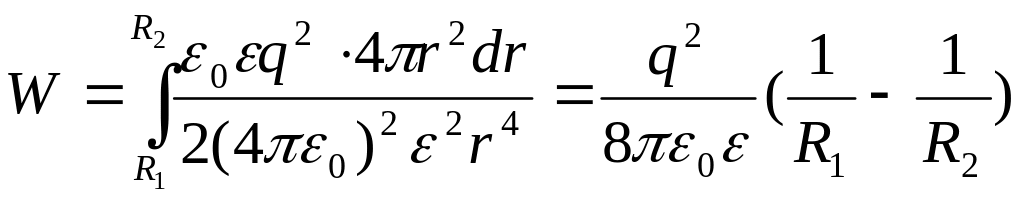(3)

Подставив числовые значения в выражение (3) и вычислив, найдём

( ).

Ответ: 135 .