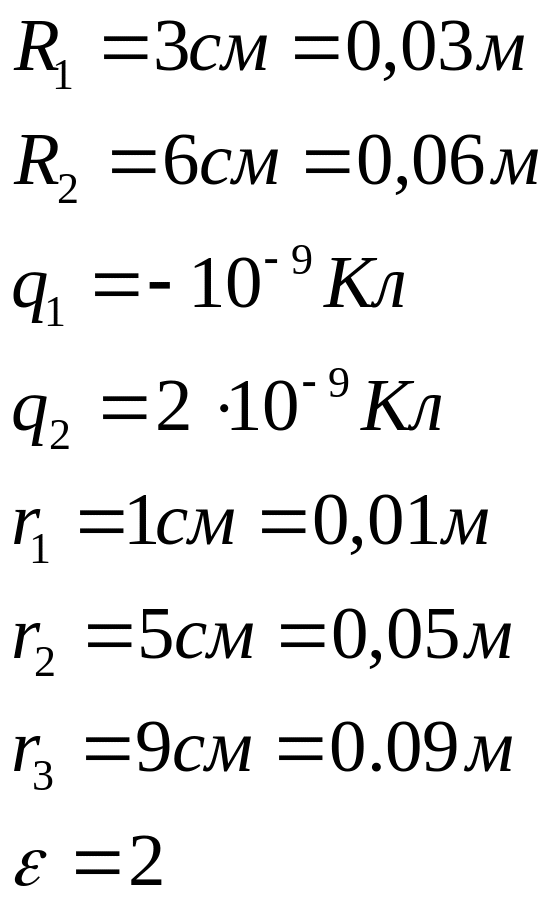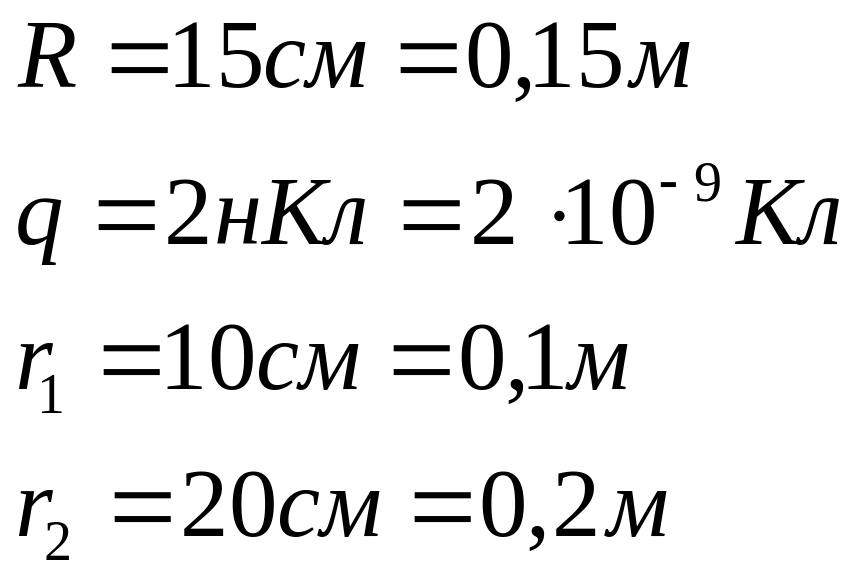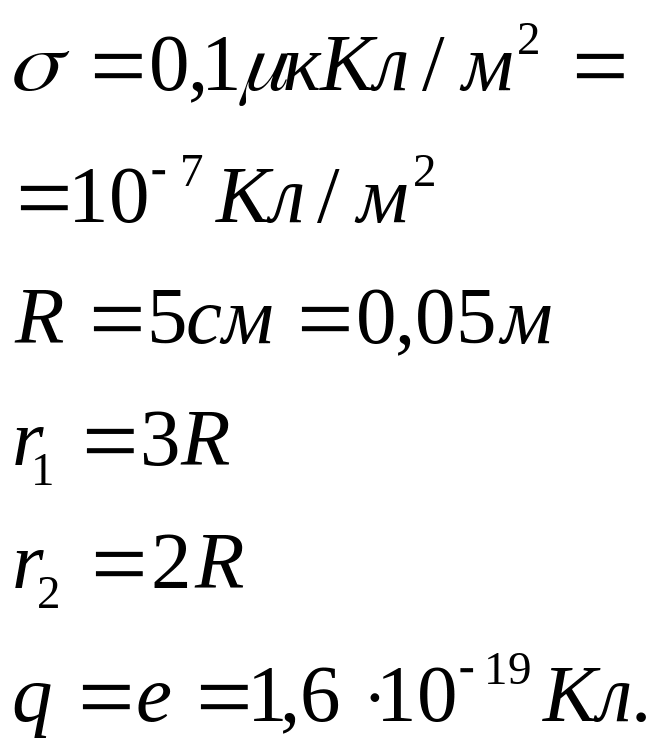- •Методические указания
- •Предисловие
- •Электростатика Основные формулы
- •1. Примеры решения задач Взаимодействие зарядов
- •Решение
- •Напряжённость
- •Решение
- •Потенциал
- •Связь напряжённости с разностью потенциалов. Вектор
- •Решение
- •Диэлектрики
- •Электроёмкость
- •Работа. Энергия системы зарядов
- •2. Задачи для самостоятельного решения
- •3. Примерные варианты для контрольных заданий
- •Библиографический список
- •Содержание
- •Методические указания
- •394026 Воронеж, Московский просп., 14
Связь напряжённости с разностью потенциалов. Вектор
З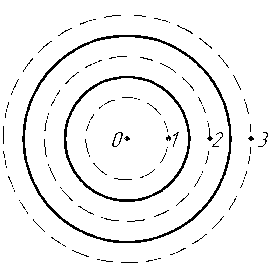 адача
1.7. Имеются две концентрические
металлические сферы радиусами
адача
1.7. Имеются две концентрические
металлические сферы радиусами
![]() и
и
![]() .
Пространство между сферами заполнено
парафином (
.
Пространство между сферами заполнено
парафином (![]() .
Заряд
внутренней
сферы равен
.
Заряд
внутренней
сферы равен
![]() ,
внешней
,
внешней
![]() =
=![]() .
Найти потенциал
.
Найти потенциал
![]() электрического поля на расстоянии: 1)
электрического поля на расстоянии: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() от центра сфер.
от центра сфер.
Дано:
|
|
П
Рис
1.7![]() и
и
![]() (рис. 1.7). Для определения напряжённостей
(рис. 1.7). Для определения напряжённостей
электрического поля в точках 1, 2, 3 воспользуемся теоремой Гаусса:
1)![]() ,
так как внутри сферы радиуса
нет электрических зарядов, поэтому
,
так как внутри сферы радиуса
нет электрических зарядов, поэтому![]() .
.
2)![]() ,
так как сфера радиуса
включает свободный заряд
,
поэтому
,
так как сфера радиуса
включает свободный заряд
,
поэтому
![]() .
Используя формулу
,
из последнего выражения получим:
.
Используя формулу
,
из последнего выражения получим:
![]()
3)![]()
![]() ,
так как сфера радиуса
проведена в вакууме и включает свободные
заряды
и
,
поэтому
,
так как сфера радиуса
проведена в вакууме и включает свободные
заряды
и
,
поэтому
![]() .
Для определения потенциалов электрического
поля в точках 1,2,3 воспользуемся формулой,
связывающей напряжённость
с потенциалом
.
Для определения потенциалов электрического
поля в точках 1,2,3 воспользуемся формулой,
связывающей напряжённость
с потенциалом
![]()
Потенциал в точке 1:
![]()
Так как
![]() (нормальная
составляющая вектора напряжённости)
терпит разрыв на всех заряженных
поверхностях, т.е. при
(нормальная
составляющая вектора напряжённости)
терпит разрыв на всех заряженных
поверхностях, т.е. при
![]() и
и
![]() ,
то последний интеграл необходимо
разобрать на два интеграла:
,
то последний интеграл необходимо
разобрать на два интеграла:
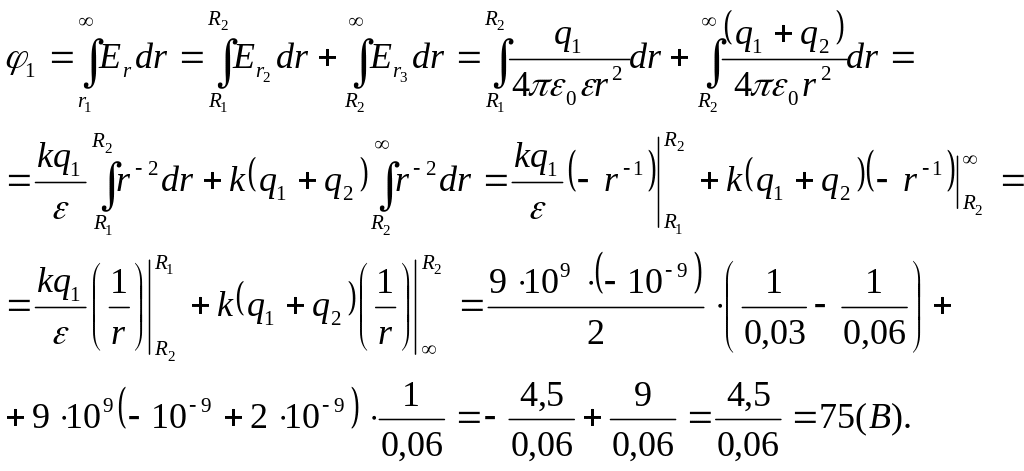 Потенциал
в точке 2:
Потенциал
в точке 2:
![]()
терпит
разрыв при
![]() ,
поэтому данный интеграл необходимо
разбить на два интеграла:
,
поэтому данный интеграл необходимо
разбить на два интеграла:
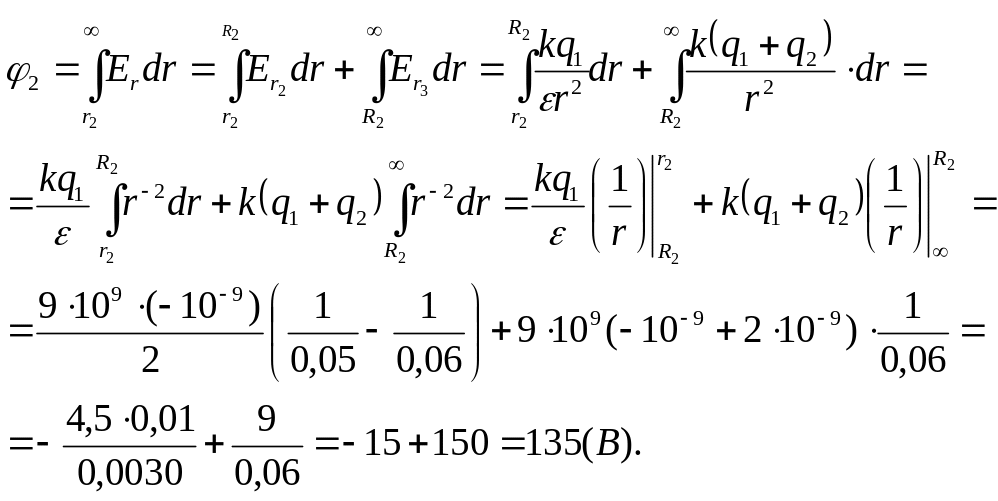
Потенциал в точке 3:
 Ответ:
Ответ:
![]()
![]()
![]()
Задача 1.8. На металлической сфере
радиусом 15 см находится заряд
![]() Определить напряженность и потенциал
электрического поля: 1) на расстоянии
Определить напряженность и потенциал
электрического поля: 1) на расстоянии
![]() от центра сферы; 2) на поверхности сферы;
3) на расстоянии
от центра сферы; 2) на поверхности сферы;
3) на расстоянии
![]() от центра сферы. Построить графики
зависимостей
от центра сферы. Построить графики
зависимостей
![]()
![]() .
.
Дано:
|
|
Точки, в которых требуется найти
напряжённость и потенциал электрического
поля, лежат в трёх областях:
![]() и
.
Для определения напряженности в
соответствующих областях воспользуемся
теоремой Гаусса:
и
.
Для определения напряженности в
соответствующих областях воспользуемся
теоремой Гаусса:
![]() .
.
Так как при (внутри сферы зарядов нет), то
![]() (1)
(1)
где
![]() сферическая поверхность радиусом
;
сферическая поверхность радиусом
;
![]() - нормальная составляющая напряжённости
электрического поля.
- нормальная составляющая напряжённости
электрического поля.
Из соображений симметрии нормальная
составляющая
должна быть равна самой напряжённости
и постоянна для всех точек сферы, то
есть
![]() .
Поэтому её можно вынести за знак
интеграла. Равенство (1) примет вид
.
Поэтому её можно вынести за знак
интеграла. Равенство (1) примет вид
![]() .
.
Так как площадь сферы не равна нулю, то
![]() ,
т. е. напряжённость поля во всех точках,
удовлетворяющих условию
,
будет равна нулю.
,
т. е. напряжённость поля во всех точках,
удовлетворяющих условию
,
будет равна нулю.
При
(поверхность сферы
![]() )
заряд равен
по условию задачи, тогда согласно теореме
Гаусса, можно записать равенство:
)
заряд равен
по условию задачи, тогда согласно теореме
Гаусса, можно записать равенство:
![]() .
.
Так как
![]() ,
то из условий симметрии следует
,
то из условий симметрии следует
![]() или
или
![]() ,
откуда
,
откуда
![]() (2)
(2)
Аналогично, при
![]() ,
,
где
![]() ,
тогда
,
тогда
![]() .
.
Потенциал электрического поля, создаваемого металлической сферой радиусом , несущей заряд , на расстоянии от центра сферы равен:
внутри сферы E =
0, потенциал одинаков и равен потенциалу
на поверхности сферы
![]()
![]() ;
;
на поверхности сферы
![]() ;
;
вне сферы
![]()
![]() .
.
Следовательно,
![]() ;
;
![]() .
.
Подставив числовые значения, получим:
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Графики зависимостей представлены соответственно на рис. 1.8 и рис. 1.9.
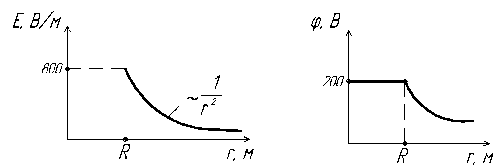
Рис. 1.8 Рис. 1.9
Ответ:![]()
![]() ,
,![]() ;
;
![]()
![]()
Задача 1.9. Электрическое поле создано
бесконечно длинным равномерно заряженным
с поверхностной плотностью заряда
![]() цилиндром радиусом
цилиндром радиусом
![]() Определить изменение потенциальной
энергии однозарядного положительного
иона при перемещении его из точки 1 в
точку 2 (рис 1.10).
Определить изменение потенциальной
энергии однозарядного положительного
иона при перемещении его из точки 1 в
точку 2 (рис 1.10).
Дано:
|
|