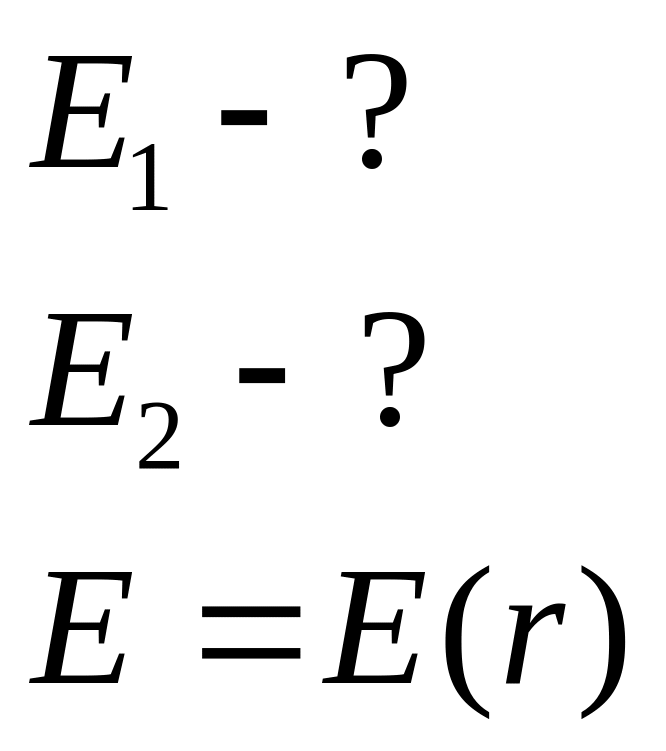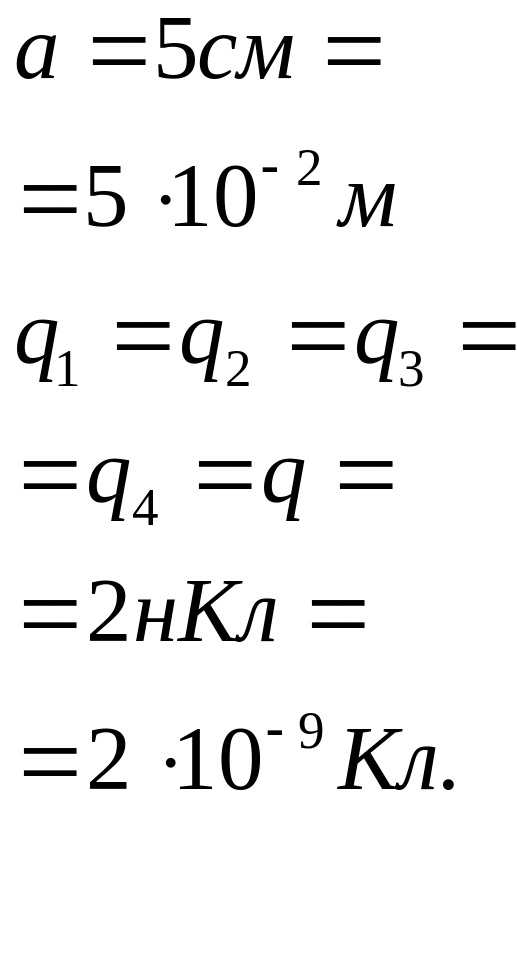Напряжённость

Задача 1.4. Кольцо из проволоки радиусом имеет отрицательный заряд . Найти напряжённости электрического поля на оси кольца в точках, расположенных от центра кольца на расстояниях , равных 0;5;8;10 и 15см. На

каком расстоянии от центра кольца напряжённость электрического поля будет иметь максимальное значение?

Дано:

при Еmax

Решение

В

Рис. 1.4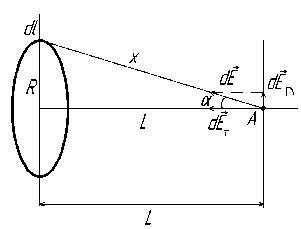

озьмём элемент кольца (рис.1.4). Этот элемент имеет заряд . Напряжённость электрического поля в точке А, созданная этим элементом,

,

где . Она направлена по линии , соединяющей элемент кольца с точкой А. Для нахождения напряжённости поля всего кольца надо векторно сложить от всех элементов. Вектор можно разложить на составляющие и . Составляющие каждых двух диаметрально противоположных элементов взаимно уничтожаются, и тогда

,

где , следовательно,

.

Из рис. 1.4 следует, что .

Окончательно получим выражение для определения напряжённости электрического поля на оси кольца в виде:

(1)

Выражение (1) – напряжённость электрического поля на оси кольца.

Если >> , то , то есть на больших расстояниях заряженное кольцо можно рассматривать как точечный заряд.

Подставляя в (1) числовые значения, получим напряжённости , равные 0; 1,60; 1,71; 1,60 и 1,15

Выразим величины и через угол : ; и формула (1) примет вид:

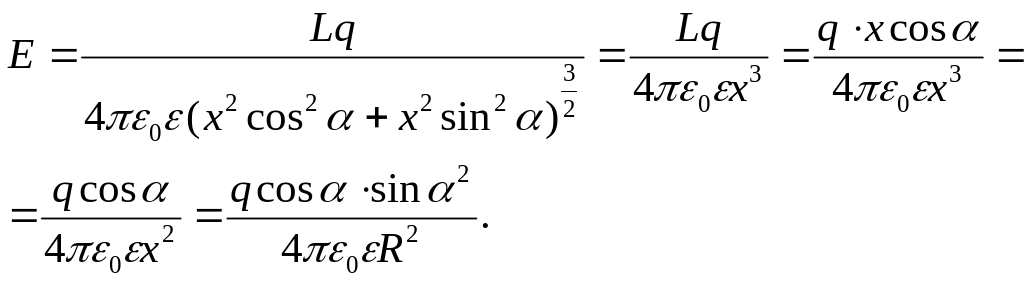
Для нахождения максимального значения напряжённости возьмём производную и приравняем её к нулю:

так как , то , . Тогда напряжённость электрического поля имеет максимальное значение в точке А, расположенной на расстоянии от центра кольца.

Ответ: ; ; ; ; ; при .

Задача 1.5. Заряд равномерно распределён по объёму шара радиусом из непроводящего материала с объёмной плотностью . Определить напряжённости поля в точках, расположенных на расстоянии от центра шара и . Построить график зависимости .

Дано:

Решение

Электрическое поле на расстоянии от центра шара создаётся только зарядами, находящимися внутри шара радиусом , так как заряженный внешний сферический слой внутри себя поля не создаёт. Заряд шара радиусом

, и на своей поверхности он создаёт поле напряжённостью

.

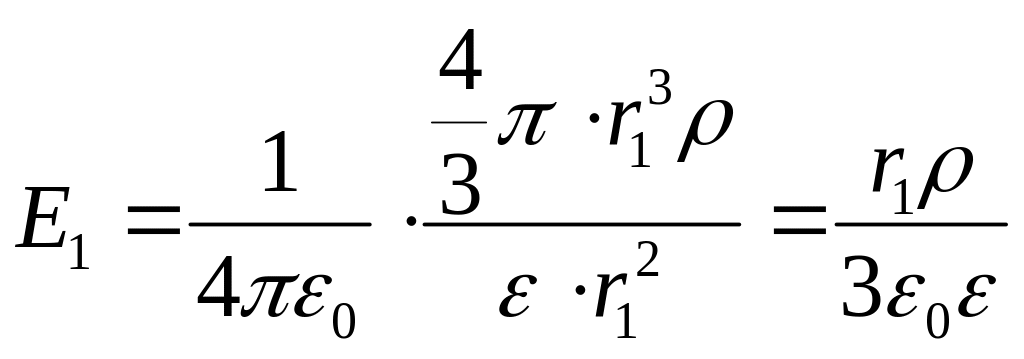Если , то электрическое поле создаётся полным зарядом шара , поэтому

.

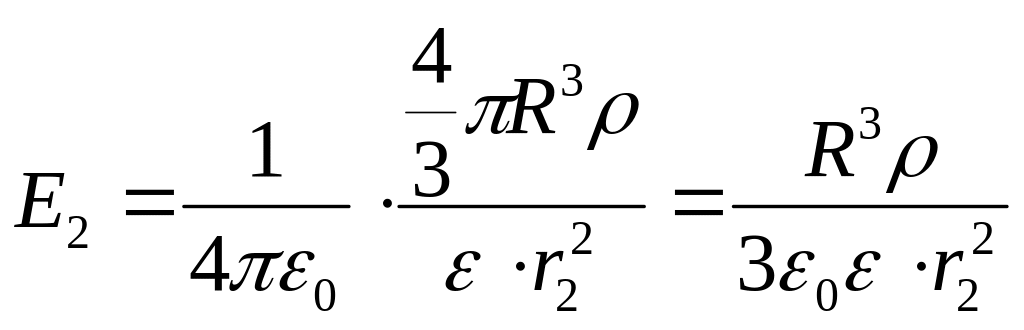
График зависимости показан на рис.1.5.

О

Рис.1.5

твет: , .

Потенциал

Задача 1.6. В вершинах квадрата со стороной 5см находятся одинаковые положительные заряды . Определить напряжённость и потенциал электрического поля: 1) в центре квадрата; 2) в середине одной из сторон квадрата.

Дано:

1) , 2) ,

Решение

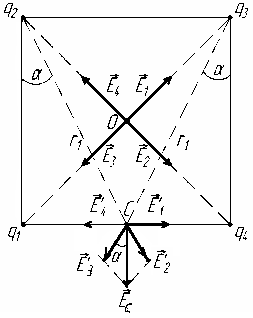
Схема расположения зарядов представлена на рис. 1.6.

Т

Рис. 1.6

ак как все заряды одинаковые и точка О (центр квадрата) находится на одинаковом расстоянии от каждого заряда , то и

напряженность равна

, то­гда , а потенциал

,

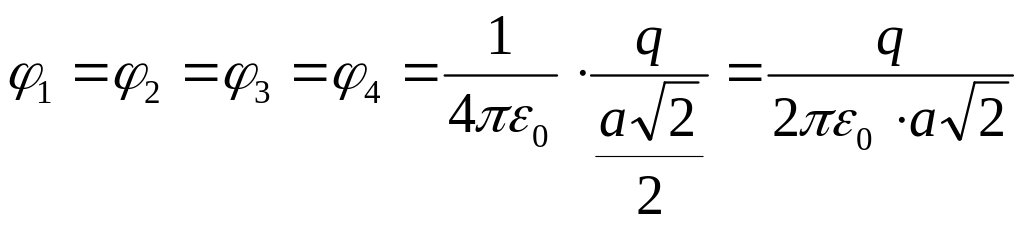тогда

.

Для точки С и их равнодействующая равна нулю.

Следовательно, , , где

Воспользовавшись свойствами ромба, найдём

, где

.

где ,

.

Следовательно,

.

Подставив числовые значения, получим:

; ;

Ответ: ; ; ; .