
- •Методические указания
- •Предисловие
- •Электростатика Основные формулы
- •1. Примеры решения задач Взаимодействие зарядов
- •Решение
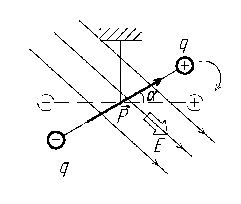
- •Напряжённость
- •Решение
- •Потенциал
- •Связь напряжённости с разностью потенциалов. Вектор
- •Решение
- •Диэлектрики
- •Электроёмкость
- •Работа. Энергия системы зарядов
- •2. Задачи для самостоятельного решения
- •3. Примерные варианты для контрольных заданий
- •Библиографический список
- •Содержание
- •Методические указания
- •394026 Воронеж, Московский просп., 14
ФГБОУ ВПО
«Воронежский государственный технический университет»
Кафедра физики
Методические указания
к решению задач по физике по теме «Электростатика»
для студентов направлений 150700.62 «Машиностроение» (профиль «Оборудование и технология сварочного
производства») и 131000.62 «Нефтегазовое дело» (профиль «Эксплуатация и обслуживание объектов транспорта
и хранения нефти, газа и продуктов переработки»)
очной формы обучения
Воронеж 2013
Составители: канд. физ.-мат. наук Н.В. Агапитова, ст. преп. П.И. Деркачева, д-р физ.-мат. наук А.В. Бугаков
УДК 681.3; 53
Методические указания к решению задач по физике по теме «Электростатика» для студентов направлений 150700.62 «Машиностроение» (профиль «Оборудование и технология сварочного производства») и 131000.62 «Нефтегазовое дело» (профиль «Эксплуатация и обслуживание объектов транспорта и хранения нефти, газа и продуктов переработки») очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. Н.В. Агапитова, П.И. Деркачёва, А.В. Бугаков. Воронеж, 2013. 48 с.
Методические указания содержат основные теоретические положения электростатики, примеры решения типовых задач с подробными пояснениями и задачи для самостоятельного решения, помогут активизировать самостоятельную работу студентов по данной фундаментальной теме курса общей физики.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2003 и содержатся в файле «Задачи по электростатике.doc».
Ил. 22. Библиогр.: 5 назв.
Рецензент д-р физ.-мат. наук, проф. Е.В. Шведов
Ответственный за выпуск зав. кафедрой канд. физ.-мат. наук, доц. Т.Л. Тураева
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
©ФГБОУ ВПО «Воронежский государственный
т ехнический
университет», 2013
ехнический
университет», 2013
Предисловие
Решение задач по различным разделам является необходимой составляющей изучения курса физики и условием выработки у студентов приёмов и навыков, помогающих им в дальнейшем решать конкретные инженерные задачи.
Электростатика – одна из фундаментальных тем физического практикума, имеющих большое значение для изучения последующих разделов физики, а также различных технических дисциплин.
Использование предлагаемых методических материалов позволит студенту в процессе индивидуальной работы усвоить материал и облегчить его понимание, сделать работу студента более комфортной и результативной.
Методические указания содержат основные теоретические положения электростатики, примеры решения типовых задач с подробными пояснениями, сборник подобных задач с ответами для самостоятельного решения, а также возможный набор вариантов для использования на практических занятиях и при отчете соответствующих тем.
.
Электростатика Основные формулы
![]() Закон
Кулона
Закон
Кулона
![]()
![]() ,
,
где F – сила взаимодействия двух точечных зарядов q1 и q2;
![]() - расстояние между зарядами,
- расстояние между зарядами,
![]() -
диэлектрическая проницаемость среды;
-
диэлектрическая проницаемость среды;
![]() -
электрическая постоянная:
-
электрическая постоянная:
=![]()
![]() /
/![]() =8,85
=8,85![]()
![]()
Закон сохранения заряда
![]()
![]() ,
,
где
алгебраическая
сумма зарядов, входящих в изолированную
систему;
![]() - число зарядов.
- число зарядов.
Напряженность электрического поля
![]() ,
,
где![]() - сила, действующая на точечный
положительный заряд
- сила, действующая на точечный
положительный заряд
![]() ,
помещенный в данную точку поля.
,
помещенный в данную точку поля.
Напряженность электрического поля, создаваемого точечным зарядом , на расстоянии от заряда
![]()
Теорема
Гаусса: поток ФЕ
вектора напряженности
![]() через любую замкнутую поверхность,
охватывающую заряды
через любую замкнутую поверхность,
охватывающую заряды
![]() ,
,
![]() ,…,
,…,
![]() :
:
ФЕ=![]() ,
,
где
![]() - алгебраическая сумма зарядов, заключенных
внутри замкнутой поверхности;
- число зарядов.
- алгебраическая сумма зарядов, заключенных
внутри замкнутой поверхности;
- число зарядов.
Принцип суперпозиции (наложения) электрических полей:
![]() ,
,
где - напряженность результирующего поля, созданного точечными зарядами.
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() - соответственно линейная, поверхностная
и объемная плотность заряда.
- соответственно линейная, поверхностная
и объемная плотность заряда.
Электрическое
смещение
![]() связано с напряженностью
электрического поля в изотропном
диэлектрике соотношением
связано с напряженностью
электрического поля в изотропном
диэлектрике соотношением
![]()
Теорема Гаусса для вектора : поток ФD вектора электрического смещения сквозь любую замкнутую поверхность, охватывающую заряды , ,…, ,
ФD=![]()
![]() ,
,
где - число зарядов (со своим знаком), заключенных внутри замкнутой поверхности.
Потенциал электрического поля – величина, равная отношению потенциальной энергии точечного положительного заряда, помещенного в данную точку поля, к этому заряду:
![]() ,
,
или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:
![]() .
.
Потенциал электрического поля, создаваемого точечным зарядом на расстоянии от заряда:
![]() .
.
Потенциал электрического поля, созданного системой точечных зарядов, в данной точке равен алгебраической сумме потенциалов, создаваемых отдельными зарядами:
![]()
Потенциал связан с напряженностью электрического поля соотношением
![]() .
.
Работа,
совершаемая электрическим полем при
перемещении точечного заряда
из одной точки поля, имеющей потенциал
![]() ,
в другую, имеющую потенциал
,
в другую, имеющую потенциал
![]()
![]()
![]() или
или
![]() ,
,
где
![]() - проекция вектора напряженности
на направление перемещения;
- проекция вектора напряженности
на направление перемещения;
![]() - перемещение.
- перемещение.
Произведение
заряда
![]() диполя на его плечо
диполя на его плечо![]() называется электрическим моментом
диполя
называется электрическим моментом
диполя
![]() .
.
Поляризованность диэлектрика
![]()
![]() ,
,
где
![]() - электрический момент отдельной
молекулы,
- электрический момент отдельной
молекулы,
![]() - число молекул, содержащихся в объеме
- число молекул, содержащихся в объеме
![]() .
.
Связь поляризованности с напряженностью среднего макроскопического поля в в изотропном диэлектрике
![]() ,
,
где
![]() - диэлектрическая восприимчивость;
- электрическая постоянная.
- диэлектрическая восприимчивость;
- электрическая постоянная.
Связь диэлектрической проницаемости с диэлектрической восприимчивостью :
![]() .
.
Напряженность
![]() среднего макроскопического поля в
диэлектрике связана с напряженностью
среднего макроскопического поля в
диэлектрике связана с напряженностью
![]() внешнего
поля соотношением
внешнего
поля соотношением
![]() и
и
![]() .
.
Механический
момент сил, действующий на диполь с
электрическим моментом
![]() ,
помещенный в электрическое поле с
напряженностью
:
,
помещенный в электрическое поле с
напряженностью
:
![]()
Электрическая ёмкость конденсатора:
![]()
![]() ,
,
где
![]() - заряд, сообщенный конденсатору
- заряд, сообщенный конденсатору
![]() - изменение потенциала, вызванное этим
зарядом.
- изменение потенциала, вызванное этим
зарядом.
Электрическая
ёмкость уединённой проводящей сферы
радиусом
![]() ,
находящейся в бесконечной среде с
диэлектрической проницаемостью
:
,
находящейся в бесконечной среде с
диэлектрической проницаемостью
:
![]() .
.
Если сфера полая и заполнена диэлектриком, то электроёмкость её от этого не изменяется.
Электрическая ёмкость плоского конденсатора
![]() ,
,
где S – площадь пластин (каждой из
пластин);
![]() -расстояние между ними;
- диэлектрическая проницаемость
диэлектрика, заполняющего пространство
между пластинами.
-расстояние между ними;
- диэлектрическая проницаемость
диэлектрика, заполняющего пространство
между пластинами.
Электрическая
ёмкость
![]() последовательно соединённых конденсаторов
последовательно соединённых конденсаторов
![]()
Электрическая ёмкость параллельно соединённых конденсаторов
![]()
Энергия
![]() взаимодействия системы точечных зарядов
,
,
…,
определяется работой, которую эта
система зарядов может совершить при
удалении их относительно друг друга в
бесконечность, и выражается формулой
взаимодействия системы точечных зарядов
,
,
…,
определяется работой, которую эта
система зарядов может совершить при
удалении их относительно друг друга в
бесконечность, и выражается формулой
![]() ,
,
где
![]() - потенциал поля, создаваемого всеми (
- потенциал поля, создаваемого всеми (![]() зарядами (за исключением
зарядами (за исключением
![]() -го)
в точке, где расположен заряд
-го)
в точке, где расположен заряд
![]() .
.
Энергия заряженного конденсатора может быть определена по одной из следующих формул:
![]() ,
,
![]() ,
,
![]() ,
,
в случае плоского конденсатора энергия равна
![]() ,
,
где
![]() - площадь каждой пластины конденсатора,
- поверхностная плотность заряда на
пластинах,
- площадь каждой пластины конденсатора,
- поверхностная плотность заряда на
пластинах,
![]() - разность потенциалов между пластинами,
- расстояние между ними.
- разность потенциалов между пластинами,
- расстояние между ними.
Объёмная плотность энергии электрического поля
![]() .
.
Сила притяжения между пластинами плоского конденсатора
![]() .
.
