
4. ЦИфровые системы автоматики
4.1. Определение дискретной системы. Разностные
уравнения
Входные и выходные сигналы непрерывных систем являются функциями непрерывного времени t.
Если
независимая переменная t
принимает только конечное множество
значений
![]() ,
то сигнал называется дискретным.
,
то сигнал называется дискретным.
Формулирование дискретного сигнала можно представить себе следующим образом (рис.4.1).
54
Рис. 4.1
g(t)![]()
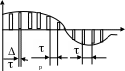


Пусть
имеется ключ Кл (рис. 4.1), который
включается на очень короткий промежуток
времени
![]() .
Если на вход такого ключа подать
непрерывный сигнал g(t),
то на его выходе образуется
последовательность импульсов g*(t).
Причём величена (амплитуда) каждого из
импульсов, будет равна амплитуде
непрерывного сигнала в дискретные
моменты
.
Если на вход такого ключа подать
непрерывный сигнал g(t),
то на его выходе образуется
последовательность импульсов g*(t).
Причём величена (амплитуда) каждого из
импульсов, будет равна амплитуде
непрерывного сигнала в дискретные
моменты
![]() .
В дальнейшем принимают, что интервал
.
В дальнейшем принимают, что интервал
![]() ,
(называемый интервалом или шагом
дискретизации по времени) является
постоянным
=const.
Поэтому для интервала наблюдения
,
(называемый интервалом или шагом
дискретизации по времени) является
постоянным
=const.
Поэтому для интервала наблюдения
![]() имеем:
имеем:
![]() ;
;
где К – целое число.
Ключ по существу является импульсным амплитудным модулятором непрерывного сигнала и называется импульсным элементом.
Известно, что непрерывные системы описываются дифференциальными уравнениями, а дискретные – разностными уравнениями.
Понятие разностного уравнения поясним на следующем примере. Предположим, что нам необходимо вычислить интеграл:
![]() (4.1)
(4.1)
55
Предположим,
что подынтегральная функция
![]() не интегрируемая в замкнутом контуре.
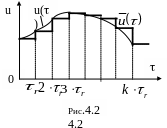
Тогда обычный прием интегрирования
заключается в том, что функция u(t)
аппроксимируется кусочно-постоянной
функцией
не интегрируемая в замкнутом контуре.
Тогда обычный прием интегрирования
заключается в том, что функция u(t)
аппроксимируется кусочно-постоянной
функцией
![]() (t)
(рис. 4.2), причём
(t)
(рис. 4.2), причём
![]() ,
,
![]()

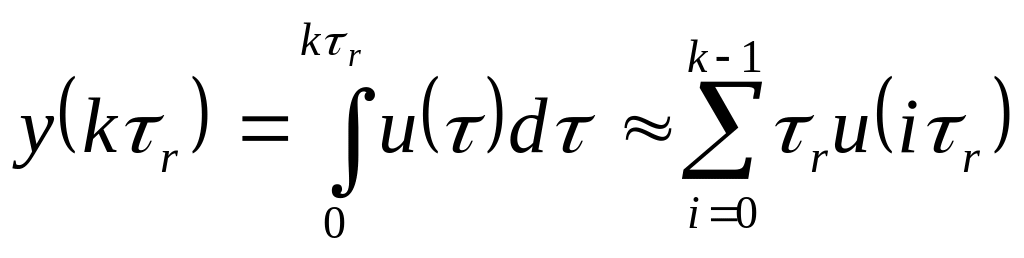 (4.2)
(4.2)
Формула
(1.2) требует запоминания всех прежних
значений сигнала
![]() для того, чтобы определить значение
интеграла в данный момент
для того, чтобы определить значение
интеграла в данный момент
![]() .
.
Гораздо более простой способ состоит в том, что вначале находят:
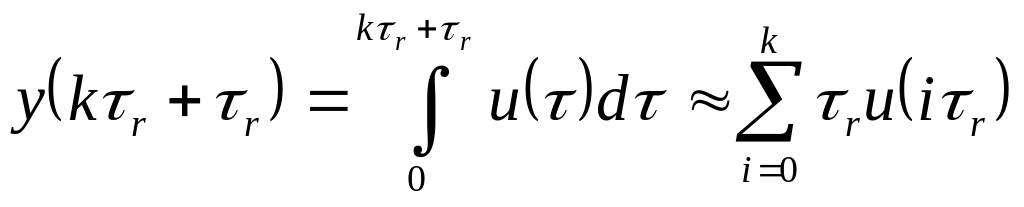 ,
(4.3)
,
(4.3)
а затем вычисляют выражение для разности (4.2) и (4.3):
56
![]() (4.4)
(4.4)
или
![]() (4.5)
(4.5)
Согласно
(4.5), необходимо запомнить только
предыдущее значение интеграла
![]() и его значение
в данный момент времени, чтобы определить
значение интеграла в последующий момент
и его значение
в данный момент времени, чтобы определить
значение интеграла в последующий момент
![]() .
.
Выражение (4.5) является разностным уравнением 1-го порядка. Алгоритм его решения заключается в следующем:
1).запоминается начальное условие: y(0)=0 – начальная сумма;
2).формулу (4.5) применяют последовательно для значений к = 0, 1, 2, …, то-есть:
![]()
![]()
![]()
…………….
![]()
На
каждом шаге этого итерационного процесса
каждое последующее значение выхода
![]() вычисляют сложением его предыдущего
значения
вычисляют сложением его предыдущего
значения
![]() c
предыдущем значением выхода
c
предыдущем значением выхода
![]() ,
умноженным на
.
,
умноженным на
.
