Задания
Вариант 1
1. Найти производные:
a)
,
если
y=ln(cos(x2+1));
б)
yIV,
если
;
в)
и
для параметрически заданной функции:
;
г)
и
для неявно заданной функции
;
2. Вычислить интегралы
а)
;
б)
;
в)
;
г)
;
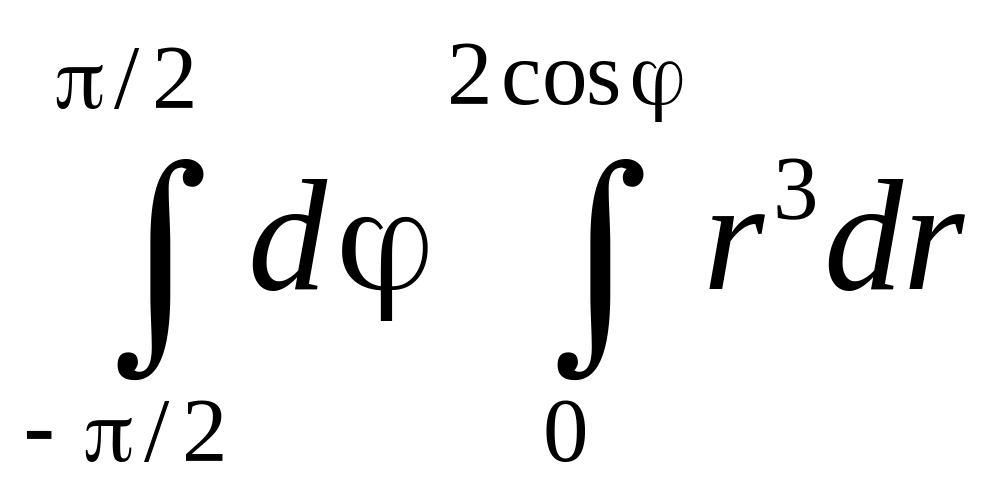3.
Найти суммы рядов: а)
;
б)
;
4. Вычислить пределы:
а)
;
б)
;
5. Выполнить операции векторного анализа:
а)
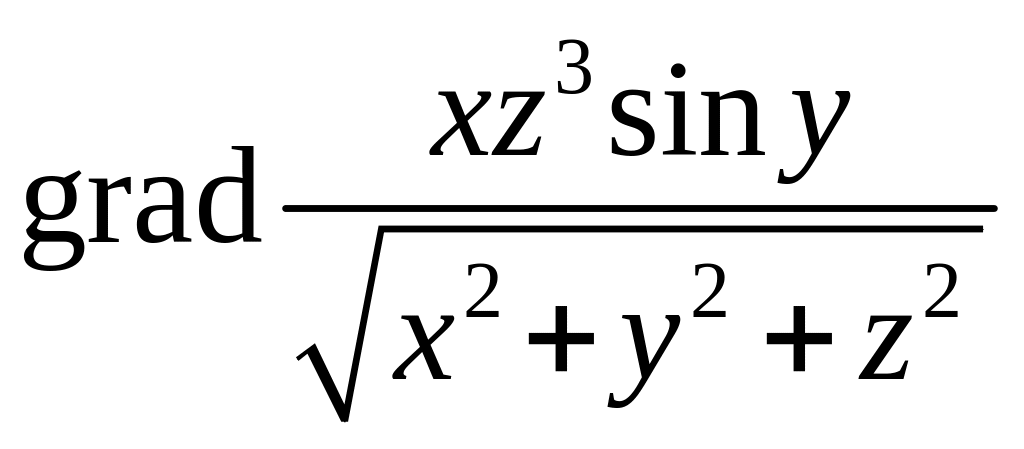в
точке
;
б)
;
в)
.
6. Построить графики функций:
a)
;
б)
.
7. Разложить функции в ряд в окрестности точки z0:
а)
;
z0=0,
б) ; z0=;
в)
.
8. Выполнить интегральные преобразования
а)
L[f(t)],
где
б)
.
9. Решить операционным методом задачу Коши
а)
,
;
б)
.
10. Найти вычеты указанных функций относительно точки z0
a)
,
z0=0;
б)
,
z0=;
в)
z0=
Вариант 2
1. Найти производные
а)
,
если
;
б)
,
если
;
в)
и
для функции, заданной параметрически:
,
;
г)
и
для функции, заданной неявно уравнением
.
2. Вычислить интегралы
а)
;
б)
;
в)
;
г)
.
3. Найти суммы рядов
а)
;
б)
4. Вычислить пределы
а)
;
б)
.
5. Решить задачи теории поля:
а) найти производную
скалярного поля
в точке A(–2,
1, 2) по направлению вектора
;
б) вычислить
дивергенцию и ротор векторного поля:
;
в) вычислить
лапласиан скалярного поля:
.
6. Найти значения функции F(x) при x=0.2, x=0.5 и x=1 и построить её график, если
а)
;
б)
;
в)
.
7.
Разложить
функцию
в ряд по степеням z–z0,
если
а)
z0=0,
б)
,
в) z0=.
8.
а)
Найти синус- и косинус-преобразования
Фурье от функции
,
заданной на интервале [0, ).
б) Найти функцию,
определенную на [0, ),
косинус-преобразование которой равно
.
9.
Найти установившееся решение
дифференциального уравнения
.
10. Разложить функцию f(t) в тригонометрический ряд Фурье на интервале (–,)
a)
б)
.
Построить графики заданной функции и частичной суммы S5(t).
Дополнительные задания
1.
Найти дивергенцию градиента функции
a)
,
б)
.
2.
а) Найти производную скалярного поля
в точке М(1,1,1)
по направлению проходящей через эту
точку нормали к поверхности
.
б) Найти производную
скалярного поля
в точке A
по направлению вектора
; A(–2,
1, 2), B(–2,
–2, 6).
3.
а) Найти угол между
и
,
если
,
M1(1;
1; 0), M2(–1;
0; 1).
б) Найти угол между
и
,
если
;
M1(1;2;3),
M2(1;1;–1).
4.
Является ли поле
,
потенциальным, соленоидальным?
5. Проверить соленоидальность поля:
.
Формулы для справок
Первая и вторая производные функции y(x), заданной параметрически:
если
x=(t),
y=(t),
то
;
.
Градиент скалярного поля и(x,y,z):
.
Производная скалярного поля и по направлению s:
=(gradu,s)=|gradи|cos,
где – угол между градиентом и единичным вектором s.
Дивергенция векторного поля a(x, y, z):
.
Ротор векторного поля а:
.
Лапласиан функции
и(x,y,z):
.
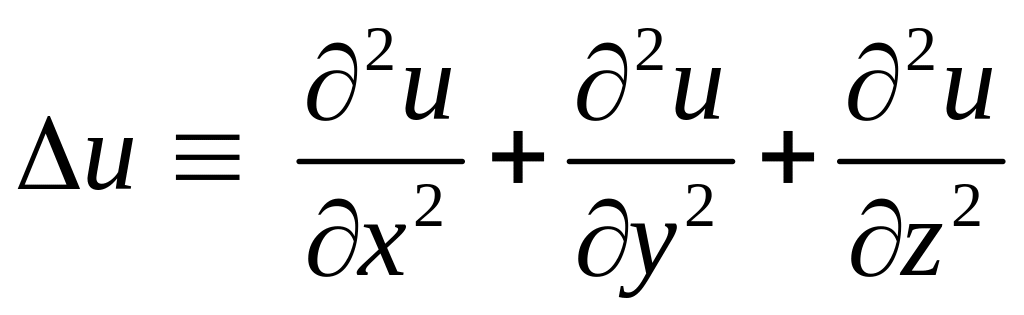Разложение в тригонометрический ряд Фурье функции f(t) на интервале (–l, l):
,
,
,
.
Ряд Фурье в комплексной форме:
,
где
(функция f(t) – 2l-периодическая).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Дьяконов В.П. Maple 7: учебный курс. СПб: Питер, 2002. – 672 с.
2. Сдвижков О. А. Математика на компьютере: Maple 8. – М.: СОЛОН-Пресс, 2003. – 176 с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление. Учеб.: В 2-х т. Т.1. Спб: Мифрил. Гл. ред. физ.- мат. лит., 1996.– 416 с.
4. Пискунов Н.С. Дифференциальное и интегральное исчисление. Учеб.: В 2-х т. Т.2. М.: Наука, Главная редакция физико-математической литературы, 1985.—560 с.
5. Бугров Я.С. , Никольский С.М. Дифференциальное и интегральное исчисление. Ростов н/Д: Феникс, 1997. – 512 с.
6. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. Ростов н/Д: Феникс, 1997. – 512 с.
7. Сборник задач по математике для втузов. В 4 частях. Ч. 2. / Под общ. ред. А.В. Ефимова, А.С. Поспелова. М.: Издательство Физико-математической литературы, 2001. – 432 с.
8. Сборник задач по математике для втузов. В 4 частях. Ч. 3. / Под общ. ред. А.В. Ефимова, А.С. Поспелова. М.: Издательство Физико-математической литературы, 2002. – 576 с.