
- •Часть 3
- •2. Место дисциплины в структуре ооп
- •3. Требования к результатам освоения дисциплины
- •A.4. Содержание дисциплины
- •Наименование тем и виды занятий
- •4.2.Содержание разделов дисциплины, изучаемых в третьем семестре
- •Раздел 6. Функциональные ряды, ряды Фурье и преобразования Фурье (16ч).
- •Лекция 62. Интеграл Фурье, преобразование Фурье и его свойства.
- •Б) дополнительная литература:
- •III семестр
- •6. Рекомендации по самостоятельному изучению разделов курса
- •7. Задания для подготовки к контрольной работе №1
- •Примеры практических заданий для подготовки к коллоквиуму
- •Задания для подготовки к контрольной работе №2
- •11. Вопросы для подготовки к экзамену
- •12. Примеры практических заданий для подготовки к сдаче экзамена
- •Часть 3
- •394026 Воронеж, Московский просп., 14
III семестр
Контрольная работа № 1 « Функциональные ряды» (7-ая неделя).
Типовой расчет № 1 «Ряды Фурье » (10-ая неделя ).
Методические указания. Сборник типовых заданий по курсу «Математический анализ» для студентов спец. 090102 «Компьютерная безопасность», 090105 « Комплексное обеспечение информационной безопасности автоматизированных систем», очной формы обучения. ВГТУ, 2010. Сост. И.Л.Батаронов, Е.Г. Глушко, А.П. Дубровская, Е.Н. Провоторова.
Коллоквиум «Функциональные ряды и ряды Фурье » (12-ая неделя).
Контрольная работа № 2 « Комплексный анализ» (16-ая неделя).
Типовой расчет № 2 « Операционное исчисление» (выдача 13-ая неделя, прием 15 неделя).
Чудесенко В.Ф. Сборник заданий по специальным курсам высшей математики. Типовые расчеты / В.Ф. Чудесенко. М., 1995.
6. Защита курсовых работ (16-17 неделя).
7. Экзамен.
6. Рекомендации по самостоятельному изучению разделов курса
Тема. Применение рядов Фурье в прикладных задачах
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления / Г.М. Фихтенгольц. М., 2001. Т.3. Гл.ХIХ п. 7.
2. . Методические указания к решению прикладных задач / сост. Е.Г. Глушко, А.П. Дубровская, Е.Н. Провоторова.
3. Бугров Я.С. Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Наука, 1989. – 464 с. Гл.5 ,п.5.6.
7. Задания для подготовки к контрольной работе №1
1. Найти область сходимости ряда:
1.
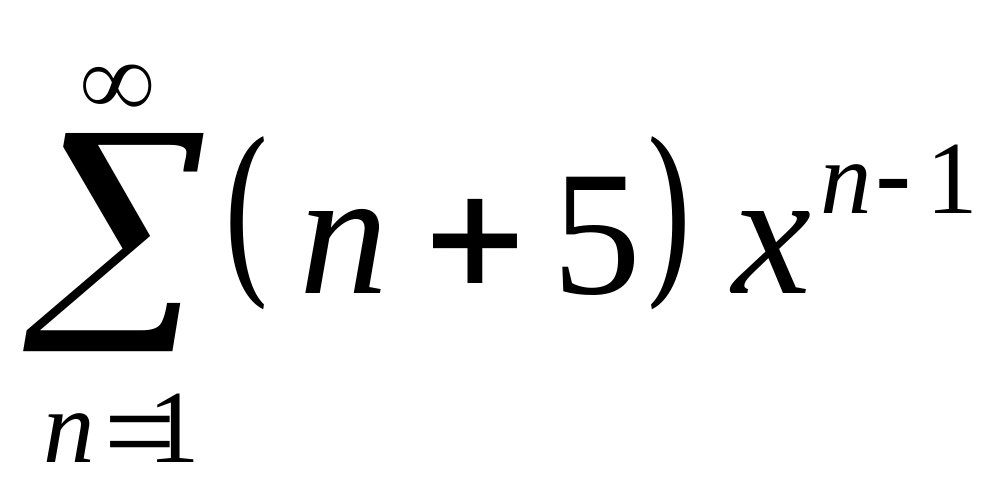 ;
2.
;
2.
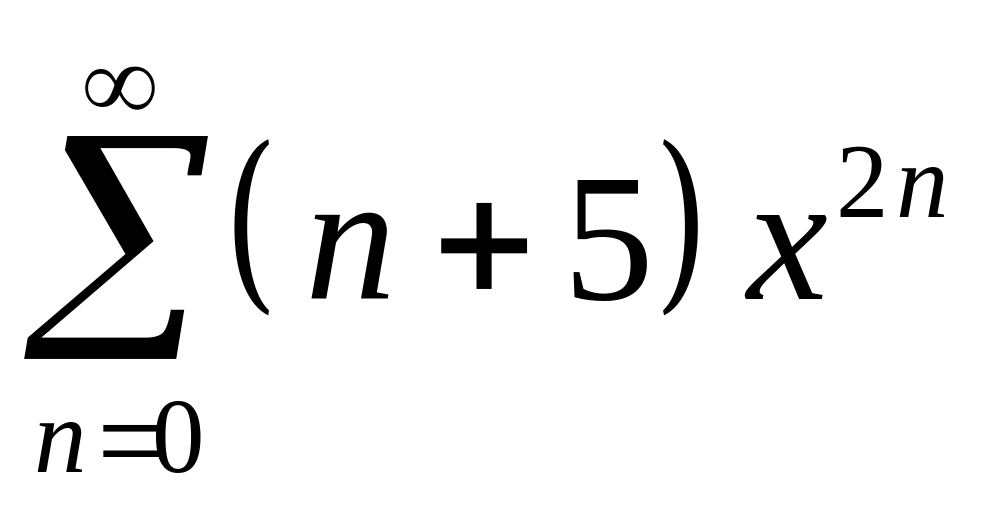 ;
;
3.
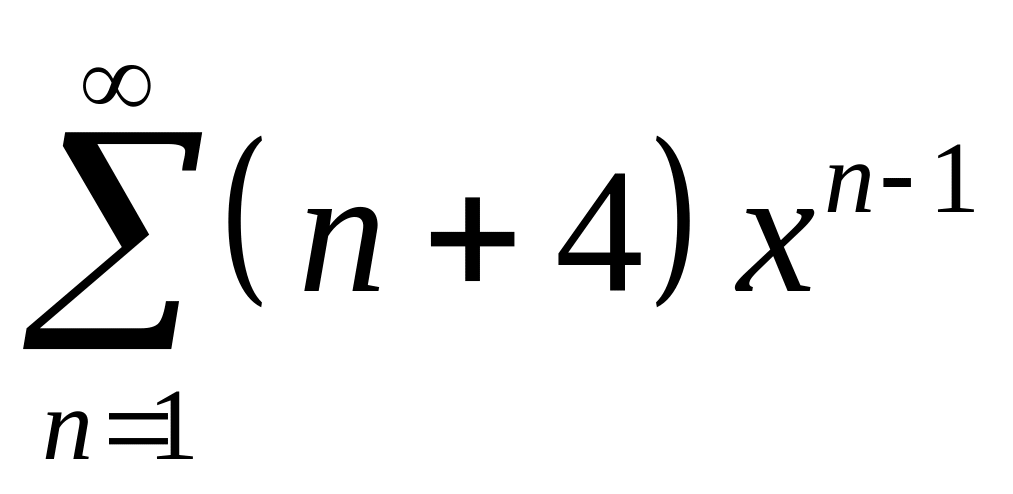 ;
4.
;
4.
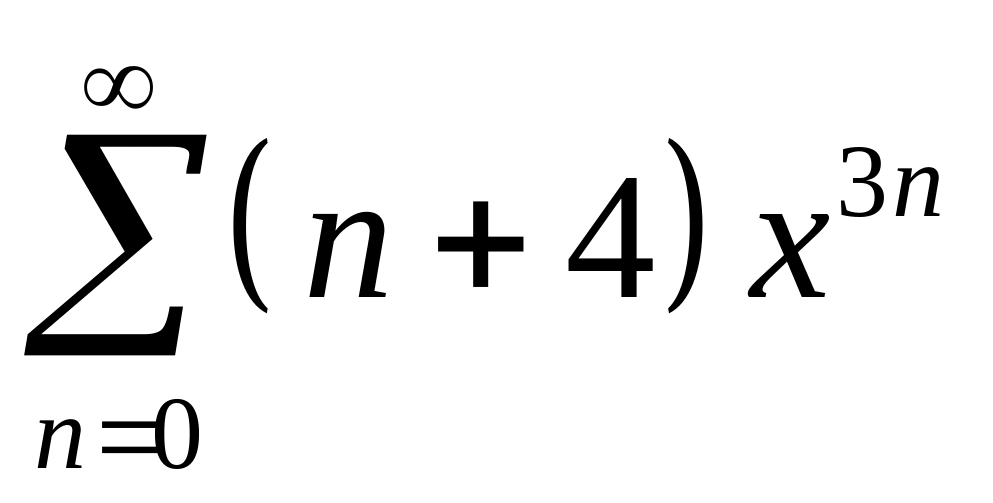 ;
;
5.
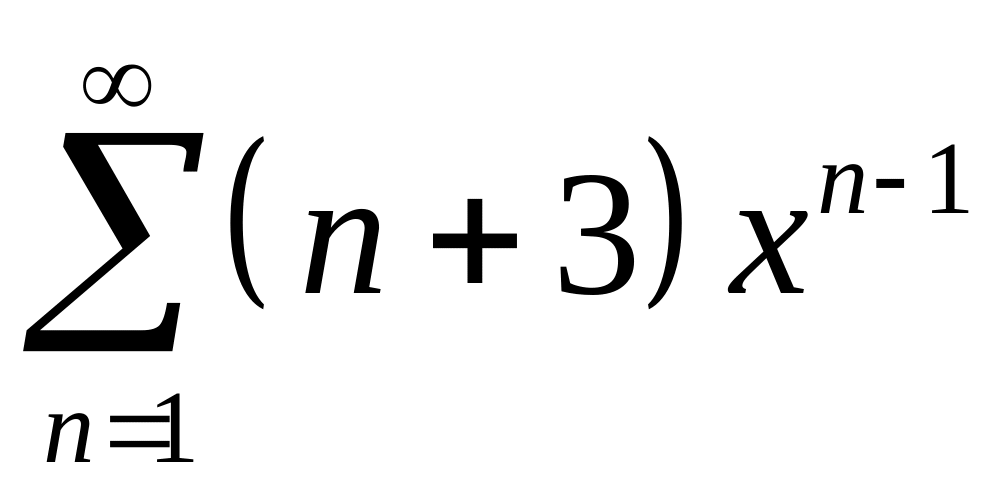 ;
6.
;
6.
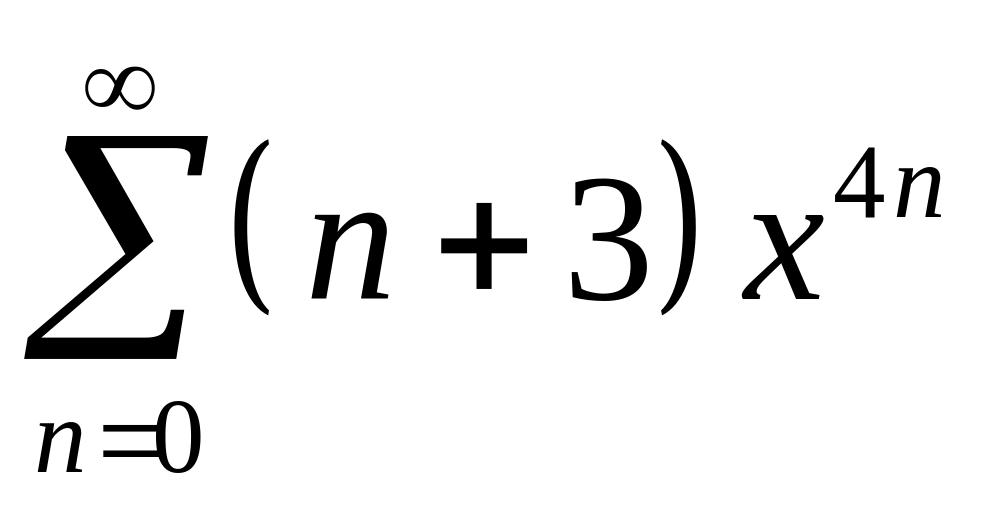 ;
;
7.
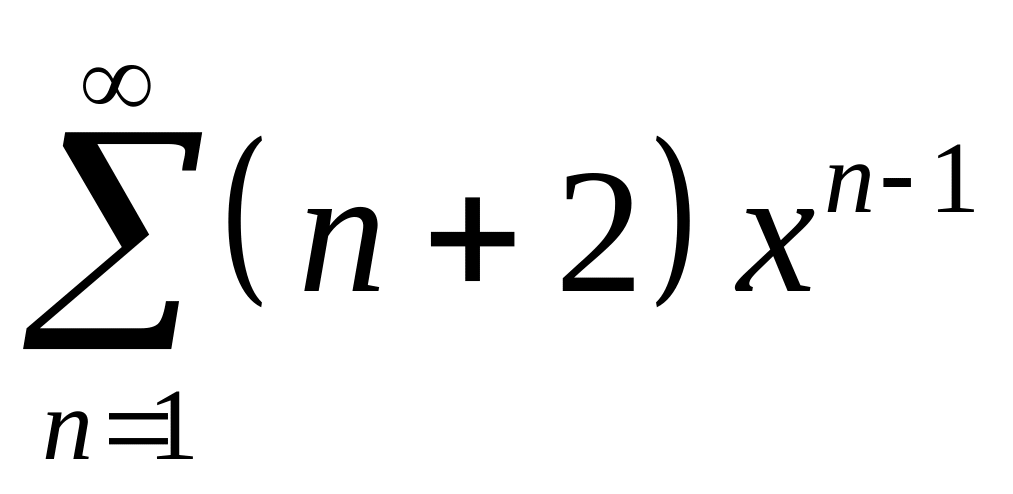 ;
8.
;
8.
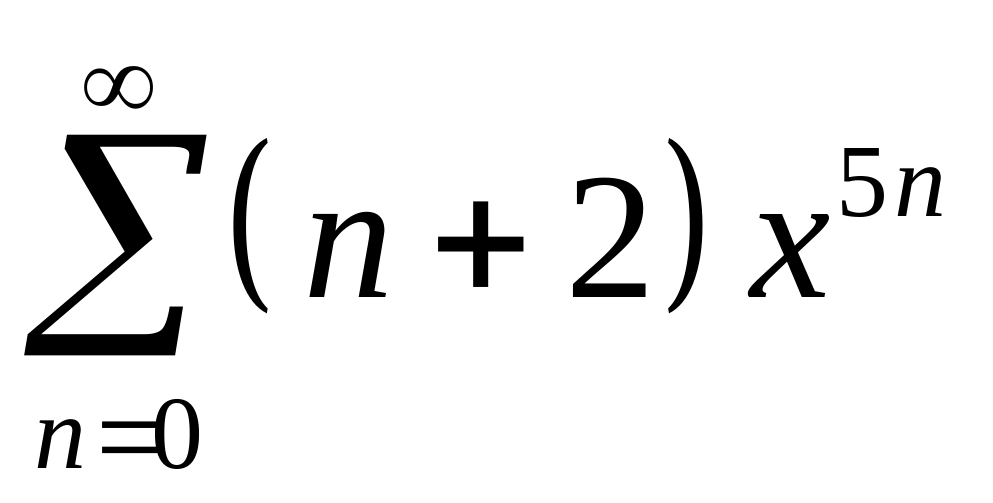 ;
;
9.
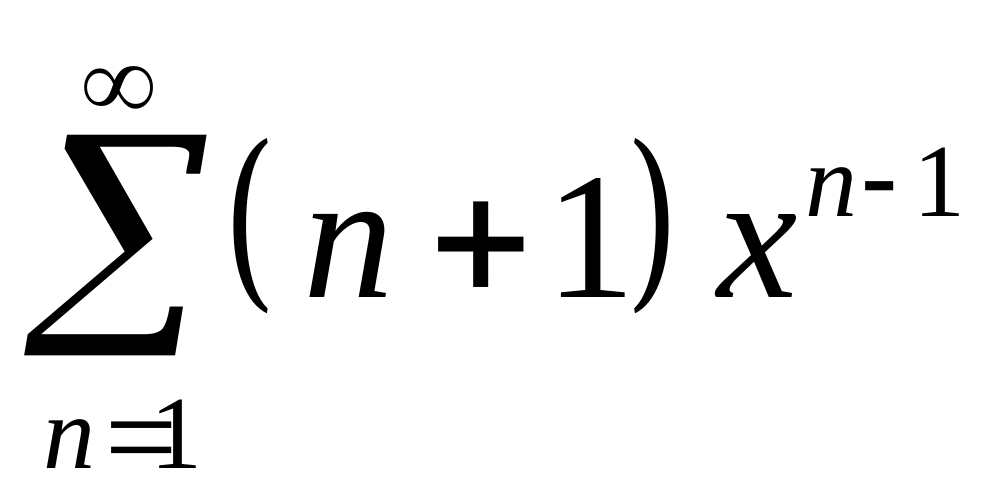 ; 10.
; 10.
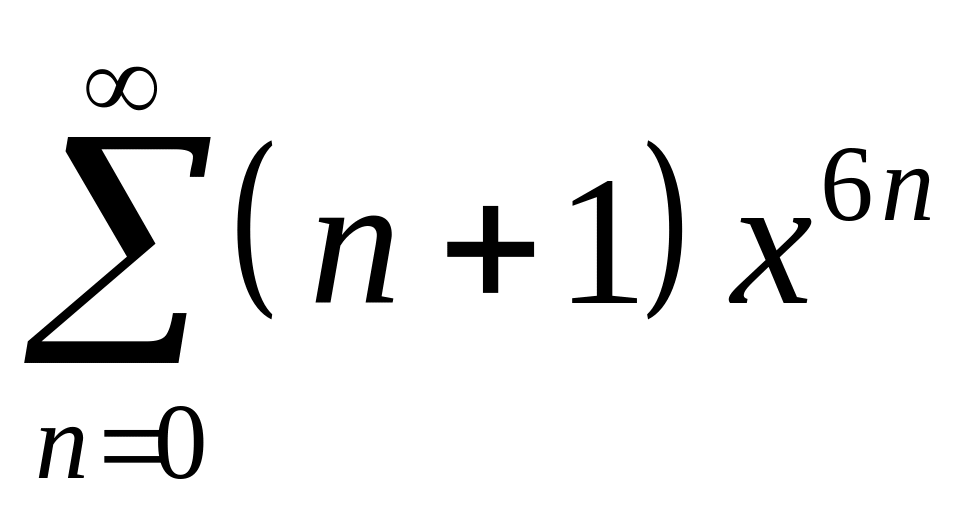 .
.
2.Разложить
функцию по степеням
![]() :
:
11.
![]() ;
12.
;
12.
![]() ;
;
13.
![]() ;
14.
;
14.
![]() ;
;
15.
![]() ;
16
;
16![]() .
.
3.Разложить
функцию по степеням
![]() :
:
17. ; 18. ;
19. ; 20. ;
21. ; 22. .
8. Вопросы для подготовки к коллоквиуму.
1. Функциональные ряды. Равномерная сходимость функциональных рядов.
2. Мажорируемость и равномерная сходимость ряда. Свойства мажорируемых рядов
3. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости.
Свойства степенных рядов.
Ряды Тейлора. Различные способы записи остаточного члена формулы Тейлора.
Разложение элементарных функций в ряды Тейлора .
7. Применение рядов Тейлора в приближенных вычислениях.
8. Периодические функции. Гармонические колебания.
9. Гильбертовы пространства. Ортогональные системы функций и ряд Фурье в гильбертовом пространстве.
10. Тригонометрическая система функций. Коэффициенты Фурье и тригонометрический ряд Фурье. Теорема о единст венности разложения функций в ряд Фурье.
11. Условие сходимости ряда Фурье. Неравенство Бесселя .
12. Основные виды сходимости классических рядов Фурье. Признаки сходимости рядов Фурье.
13. Ряды Фурье для четных и нечетных функций.
14. Ряд Фурье для функций, заданных на произвольном промежутке.
15. Представление непериодических функций рядом Фурье.
16. Ряд Фурье в комплексной форме.
17. Интеграл Фурье, преобразование Фурье и его свойства.
18. Интеграл и преобразования Фурье в комплексной форме. Примеры отыскания спектральных характеристик преобразования.
