
- •ВВЕДЕНИЕ
- •Пособие по интегральному исчислению предназначено для студентов заочной формы обучения, но, безусловно, может быть использовано и студентами дневной формы всех специальностей ВГАСУ.
- •Без интегралов не может обойтись ни физика, ни химия, ни теоретическая механика, ни строительная механика и т.д. и т.п., а значит, практически все инженерные дисциплины.
- •Авторы настоятельно советуют внимательно читать и разбирать теоретические вопросы, прежде чем использовать полученные формулы для вычисления интегралов (их использование достаточно простое для читателя, освоившего первую главу).
- •Во второй и третьей главах подробно разобрано множество примеров и задач, объясняется выбор формулы при решении каждой задачи.
- •Авторы надеются, что данное пособие поможет читателям в освоении материала – сложного и очень важного для дальнейшего обучения.
- •1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- •1.1. Первообразная и неопределенный интеграл
- •Свойство 1.1. Производная от неопределенного интеграла равна подынтегральной функции:
- •Свойство 1.3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной
- •1.2. Таблица интегралов
- •1. Если
- •3. Если
- •Воспользовавшись формулой 3 таблицы интегралов и формулой (1.11) (a = 2, b = -6) получим
- •Обозначим:
- •Тогда
- •По формуле (1.12) получим
- •1.6. Интегрирование рациональных функций
- •1.8. Интегралы от некоторых иррациональных выражений
- •I. Рассмотрим интеграл вида
- •2.1.2. Определение определенного интеграла
- •2.1.3. Свойства определенного интеграла
- •2.1.4. Интеграл с переменным верхним пределом
- •2.1.5. Формула Ньютона-Лейбница
- •2.1.6. Замена переменной в определенном интеграле
- •2.1.7. Интегрирование по частям в определенном интеграле
- •2.1.8. Геометрические приложения определенного интеграла
- •2.1.8.5. Объем тел вращения
- •2.2. Несобственные интегралы
- •3.1. Двойные интегралы
- •3.1.1. Задача об объеме цилиндрического тела
- •3.1.2. Задача о массе неоднородной пластинки
- •3.1.3. Определение двойного интеграла
- •Имеем
- •Вопросы и задания для самоконтроля
- •1. Какие из перечисленных интегралов можно найти только с помощью формулы интегрирования по частям:
- •4. Что такое универсальная подстановка?
- •7. Чем отличаются формулы интегрирования по частям в неопределенном и определенном интегралах?
- •8. Какие из перечисленных интегралов являются несобственными:
данном примере |
u = x , |
поэтому du = |
х′ |
dx = dx. В качестве dv мы взяли |
||||||||||||
dv = sin 2xdx |
поэтому |
ищем |
|
∫dv = ∫sin 2xdx = − |
1 cos2x + C |
и берем, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
например, v = −1 cos2x . Итак, u = x , dv = sin 2xdx и du = dx, v = − |
1 cos2x . По |
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
формуле (1.12) |
∫udv = uv − ∫vdu , т.е. |
|
|
|
|
|
|
|
|
|||||||
|
|
∫xsin 2xdx |
|
1 |
|
|
|
|
− |
1 |
|
|
|
|||
|
|
= x − |
2 |
cos2x |
− ∫ |
2 |
cos2x dx = |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= − |
xcos2x |
|
+ 1 |
∫cos2xdx = − |
xcos2x |
+ |
1 |
1 sin 2x + C . |
|
|||||||
|
|
|
||||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|
2 |
|
|
2 |
2 |
|
Окончательно |
|
|
∫xsin 2xdx = − 1 xcos2x + 1 sin 2x + C . |
|
||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
Иногда для «освобождения» от одного из множителей в |
||||||||||||||||
подынтегральном |
выражении |
|
приходится |
|
применять |
формулу |
||||||||||
интегрирования по частям несколько раз. |
|
|
|
|
|
|
||||||||||
Пример 1.23. Вычислить интеграл ∫(x2 |
+ 7x − 5)ex dx . |
|
||||||||||||||
Обозначим: |
|
|
|
|
|
|
+ 7x − 5)′ dx = (2x + 7)dx , |
|
||||||||
u = x2 + 7x − 5, |
dv = ex dx ; тогда du = (x2 |
|
||||||||||||||
v = ∫ex dx = ex + C (C = 0).
По формуле (1.12) получим
∫(x2 + 7x − 5)ex dx = (x2 + 7x − 5)ex − ∫(2x + 7)ex dx .
Кполученному в правой части интегралу снова применим формулу интегрирования по частям, где
u = 2x + 7 , dv = ex dx ; du = 2dx , v = ex .
Тогда
∫(2x + 7)ex dx = (2x + 7)ex − 2∫ex dx = (2x + 7)ex − 2ex + C .
Окончательно
∫(x2 + 7x − 5)ex dx = (x2 + 7x − 5)ex − (2x + 7)ex + 2ex + C =
=ex (x2 + 7x − 5 − 2x − 7 + 2)+ C = ex (x2 + 5x −12)+ C .
22
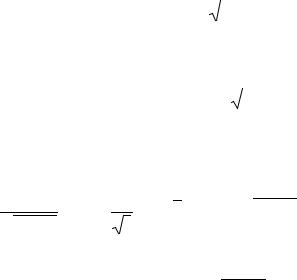
Пример 1.24. Вычислить интеграл ∫x2 ln xdx .
В данном интеграле избавимся от функции ln x . |
Применим формулу |
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
′ |
|
dx |
2 |
|
x3 |
|
||
(1.12), где u = ln x , |
dv = x |
|
dx |
; тогда |
du = (ln x) |
dx = |
x |
, v = ∫x |
dx = |
|
+ C |
||||||
|
3 |
||||||||||||||||
(возьмем C = 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По формуле (1.12) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫x2 ln xdx = |
x3 |
ln x − ∫ |
x3 |
dx |
= |
x3 |
ln x − 1 ∫x2 dx = |
x3 |
ln x − |
x3 |
+ C . |
|
|
||||
|
|
|
3 |
|
|
|
|||||||||||
3 |
|
|
3 |
x |
3 |
3 |
|
9 |
|
|
|
|
|||||
Пример 1.25. Вычислить интеграл ∫x arctg x dx .
Избавимся от функции arctg x, применив формулу (1.12). Положим
u = arctgx , dv = xdx , du = |
|
dx |
, |
v = ∫xdx = |
x2 |
+ C (C = 0 ). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 + x |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда будем иметь по формуле (1.12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∫x arctg x dx = |
|
x2 |
arctg x − ∫ |
x2 |
|
|
dx |
|
= |
x2 |
arctg x − 1 ∫ |
|
x2 dx |
= |
||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
(x2 +1)−1 |
2 |
|
1 + x |
2 |
|
|
|
2 |
|
|
1 + x |
|
|
|||||||||||||
= |
|
x2 |
|
arctg x − |
1 |
∫ |
dx = |
|
x2 |
arctg x − |
1 |
∫dx + |
1 |
∫ |
|
|
|
dx |
|
= |
||||||||||||||||
|
2 |
|
|
2 |
|
1 + x |
2 |
|
|
2 |
2 |
2 |
1 |
+ x |
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
x2 |
|
arctg x − |
x |
|
+ |
1 arctg x + C = |
1 |
(x2 arctg x − x + arctg x)+ C . |
|||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 1.26. Вычислить интеграл ∫arcsin xdx . |
|
|
|
|
|
|
arcsin x , |
||||||
В подынтегральном выражении |
|
|
стоит функция |
||||||||||
первообразная от которой неизвестна, |
избавимся от этой функции, применив |
||||||||||||
формулу (1.12), |
|
|
|
|
|
|
|
|
|
|
|
|
|
u = arcsin x , dv = dx |
, du = |
|
|
dx |
|
|
, |
v = x . |
|
||||
|
|
|
|
|
|
|
|
||||||
1 − x2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
Тогда по формуле (1.12), получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
∫arcsin xdx = xarcsin x − ∫ |
|
|
xdx |
|
|
. |
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
1 − x |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
В последнем интеграле сделаем замену: t =1 − x2 , |
dt = −2xdx , xdx = −dt , |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
при этом
∫
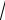 1xdx− x2 = −12∫ dtt = −
1xdx− x2 = −12∫ dtt = −
 t + C = −
t + C = −
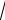 1 − x2 + C .
1 − x2 + C .
Окончательно получаем
∫arcsin xdx = xarcsin x + 
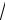 1 − x2 + C .
1 − x2 + C .
23
Иногда подынтегральная функция – это произведение двух «плохих» функций, от которых нельзя избавиться, т.к. их производные не лучше, чем сами функции. В некоторых случаях двукратное применение формулы (1.12) позволяет выразить искомый интеграл через самого себя. В итоге получается линейное уравнение относительно искомого интеграла.
Пример 1.27. Вычислить интеграл I = ∫e2 x cos xdx .
В подынтегральном выражении произведение двух «плохих» функций e2 x и 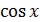 . Применим формулу (1.12), где
. Применим формулу (1.12), где
u = e2 x , dv = cos xdx ; тогда du = 2e2 x dx , v = sin x .
Получим
I= ∫e2 x cos xdx = e2 x sin x − 2∫e2 x sin xdx .
Кинтегралу в правой части равенства снова применим формулу интегрирования по частям, взяв u = e2 x , dv = sin xdx ; du = 2e2 x dx , v = −cos x .
Тогда ∫e2 x sin xdx = −e2 x cos x + 2∫e2 x cos xdx = −e2 x cos x + 2I .
Подставляя полученное выражение в предыдущее равенство, имеем
I = e2 x sin x − 2(− e2 x cos x + 2I ).
Получилось линейное уравнение относительно I :
I = e2 x (sin x + 2cos x)− 4I , откуда 5I = e2 x (sin x + 2cos x).
Учитывая, что I – это неопределенный интеграл, имеем
I = ∫e2 x cos xdx = e2 x sin x + 2e2 x cos x + C . 5
Все методы интегрирования исчерпываются рассмотренными ранее методами замены переменной, интегрирования по частям и использованием свойств неопределенного интеграла. Далее мы рассмотрим некоторые классы функций, для интегрирования которых разработан план применения методов интегрирования.
1.6. Интегрирование рациональных функций
Рациональная функция, обозначаемая R(x),- это функция, представимая в виде рациональной дроби, т.е. в виде отношения двух многочленов:
Q(x) |
|
B0 xm + B1 xm−1 + + Bm |
|
|
|
= |
A0 xn + A1 xn−1 + + An . |
f (x) |
|||
Не ограничивая общность рассуждения, будем предполагать, что эти многочлены не имеют общих корней.
24

Если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе, то дробь называется правильной, а в противном случае дробь называется неправильной.
Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:
Q(x) |
= M (x)+ |
F(x) |
. |
|
f (x) |
|
|
||
|
f (x) |
|||
Здесь M(x) – многочлен, называемый целой частью неправильной дроби, а
F((x)) – правильная дробь. f x
Пример 1.28. Преобразовать неправильную рациональную дробь
x4 − 3 |
(4 > 2). |
x2 + 2x +1 |
Разделив числитель на знаменатель (по правилу деления многочленов), получим
|
x4 − 3 |
|
= x2 |
− 2x + 3 − |
|
4x + 6 |
|
. |
|
x2 + 2x +1 |
|
x2 + 2x +1 |
|||||
|
|
|
|
|
||||
Здесь x2 − 2x + 3 – целая часть |
дроби, а |
− (4x + 6) – остаток от деления |
||||||
числителя на знаменатель.
Проинтегрировать многочлен просто, поэтому основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей.
|
|
|
Определение 1.3. Правильные рациональные дроби вида: |
||||||
I. |
|
|
A |
; |
|
|
|
|
|
x − a |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
A |
|
|
|
|
||
II. |
|
|
|
( k |
– целое положительное число ≥ 2); |
|
|
||
|
(x − a)k |
|
|
||||||
III. |
|
Ax + B |
|
(корни знаменателя комплексные, т.е. |
p2 |
− q < 0); |
|||
|
x2 + px + q |
4 |
|||||||
|
|
|
|
|
|||||
IV. |
|
|
Ax + B |
|
, k ≥ 2 |
|
|
||
|
(x2 |
+ px + q)k |
|
|
|||||
называются простейшими дробями.
При интегрировании дробей типа I, II, используются табличные интегралы 1, 2 и формула (1.10). Интегрирование дробей типа III было подробно рассмотрено ранее в п. 1.5. Поэтому мы повторим кратко их интегрирование без каких-либо дополнительных пояснений:
25

I. ∫ |
|
|
|
|
|
A |
|
|
dx = Aln |
|
|
|
x − a |
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x − a |
|
|
|
|
|
|
(x − a)−k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
II. ∫ |
|
|
|
|
|
|
|
A |
|
|
|
|
dx = |
A∫(x − a)−k dx = A |
+ C = |
|
|
|
|
|
|
A |
|
|
|
|
|
|
+ C . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
(x − a) |
k |
|
− k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k −1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 − k)(x − a) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ax + B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + B |
|
|
|
|
|
|
|
|
|
A |
|
|
|
2x |
+ 2B |
|
|
|
A |
|
|
|
(2x + p)+ |
2B |
− p |
|
|||||||||||||||||||||||||||
III. ∫ |
|
|
|
|
|
dx = A∫ |
|
|
|
|
|
|
|
A |
|
|
|
|
dx = |
|
∫ |
|
|
|
|
|
|
|
A |
|
= |
∫ |
|
|
|
|
|
|
|
A |
|
dx = |
|||||||||||||||||||||||||||||||||||||
|
x |
2 |
|
|
|
|
x |
2 |
+ px + q |
|
2 |
|
x |
2 |
+ px + q |
|
|
|
|
|
|
x |
2 |
+ px + q |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ px + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
A |
|
|
|
|
|
(2x + p)+ 2AB − p |
|
|
|
|
|
|
|
A |
|
|
|
(2x + p) |
|
|
|
|
|
|
|
|
|
Ap |
|
|
|
|
|
|
dx |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
dx + |
|
B − |
|
|
∫ |
|
|
|
|
|
|
|
|
|
= |
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
x |
2 |
|
|
+ px + q |
2 |
x |
2 |
|
+ px + q |
|
2 |
|
x |
2 |
+ px + q |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
A |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ap |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
|
|
|
|
|
ln |
x |
|
+ px + q |
|
+ B |
− |
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= = |
|
|
|
ln |
x |
|
+ px + q |
+ |
|
|
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
p |
2 |
|
|
|
|
|
|
p |
2 |
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+ |
|
|
|
+ |
|
q − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+ |
2 |
B − Ap |
|
|
|
arctg |
|
|
|
2x + p |
|
|
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
4q − p2 |
|
|
|
|
|
|
|
|
4q − p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Теперь научимся интегрировать рациональные дроби IV типа: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫ |
|
|
|
|
|
|
Ax + B |
|
|
|
, |
|
(k N, |
|
k ≥ 2), |
где корни квадратного трехчлена x2 + px + q |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(x |
2 |
|
+ px + q) |
k |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
комплексные. При интегрировании такой дроби сначала делаются такие же преобразования, что и для дробей типа III: в числителе выделяется производная квадратного трехчлена, а затем дробь разбивается на сумму двух слагаемых:
Ax + B
(x2 + px + q)k
=A2
|
|
|
x + B |
|
|
|
|
A |
|
(2x + p)− p + |
B |
||||
= A |
|
A |
|
|
= |
|
|
|
|
|
|
A |
= |
||
(x2 |
+ px + q)k |
2 |
|
|
(x2 + px + q)k |
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
(2x + p) |
|
|
|
B − |
pA |
|
|
|||||||
|
+ |
|
|
2 |
|
. |
|
|
|||||||
(x2 + px + q)k |
(x2 + px + q)k |
|
|
||||||||||||
При интегрировании |
первого |
слагаемого |
делаем замену t = x2 + px + q , |
dt = (2x + p)dx , а во |
втором |
слагаемом |
выделяем полный квадрат в |
квадратном трехчлене. |
|
|
|
26

Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax + B |
|
|
|
A |
|
dt |
|
|
|
|
pA |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
||||||||
∫ |
|
|
|
|
|
|
|
= |
|
|
|
∫ |
|
|
+ B − |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||
(x |
2 |
+ px + q) |
k |
2 |
t |
k |
|
2 |
|
|
|
p 2 |
|
|
|
p2 |
|
k |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
|
+ q − |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||
|
|
|
|
A |
|
t−k +1 |
|
|
|
|
|
|
|
pA |
|
|
|
|
|
d x + |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
= |
|
|
|
|
|
|
|
+ B − |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
|
|
|
2 |
− k |
+1 |
2 |
|
|
|
|
|
p |
|
|
|
|
p2 |
|
k |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
+ q |
− |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для того чтобы найти последний интеграл, применяют рекуррентную формулу
|
dx |
|
|
1 |
|
|
x |
|
|
|
dx |
|
|
|
|
|
Ik = ∫ |
|
= |
|
|
+ |
(2k −3)∫ |
|
|
, |
(1.13) |
|
|||||
(x2 +h2 )k |
2(k −1)h2 |
|
|
(x2 + h2 )k −1 |
(x2 |
+h2 )k −1 |
|
|
||||||||
позволяющую |
интеграл Ik |
|
( k > 1) |
выразить |
через |
|
Ik −1 = ∫ |
dx |
. |
|||||||
|
|
(x2 + h2 )k −1 |
||||||||||||||
Применяют эту формулу столько раз, чтобы дойти до интеграла ∫ x2 dx+ h2 , являющегося табличным (формула 11').
Пример 1.29. Найти интеграл ∫(x2 dx+ 4)2 .
|
|
|
dx |
|
|
по формуле (1.13) |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫(x2 + 4)2 = |
|
|
|
k = 2, h2 = 4 |
|
|
|
|
= |
2(2 −1) |
4 |
(x2 + 4)2−1 + (2 |
2 − 3)∫(x2 + 4)2−1 |
|
= |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
= |
1 |
|
|
|
|
|
x |
|
+ ∫ |
|
|
|
dx |
|
|
= |
1 |
|
x |
|
|
|
+ |
1 |
arctg |
x |
|
+ C . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
8 |
|
|
2 |
+ 4 |
|
x |
2 |
|
|
|
|
|
8 |
|
2 |
+ |
4 |
|
2 |
2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
+ 4 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Пример 1.30. Найти интеграл ∫ |
|
(3x + 2)dx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x + 2x + 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
(3x + 2)dx |
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
3 |
|
|
|
(2x + 2)+ |
3 |
− 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
∫ |
|
|
|
= |
3∫ |
|
|
|
|
|
|
|
|
dx = |
∫ |
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
||||||||||||||||||||||||||
|
(x |
2 |
|
|
|
|
|
|
|
2 |
(x |
2 |
+ |
2x + |
|
|
2 |
2 |
|
|
(x |
2 |
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
+ 2x + 2) |
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
+ 2x + 2) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
∫ |
|
|
|
|
(2x + 2) |
|
|
|
dx + |
3 |
|
|
2 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
∫ |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
(x |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
+ 2x + 2) |
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
(x |
+ |
2x + 2) |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
в первом слагаемом замена x2 |
+ 2x + 2 = t, |
dt = (2x + 2)dx, |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
а во втором выделяем полный квадрат в квадратном |
|
= |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
трехчлене x2 |
+ 2x + 2 = (x +1)2 |
+1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
27
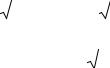
|
|
3 dt |
|
|
|
dx |
|
|
|
|
|
|
3 1 |
|
|
|
d (x +1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= 2 |
∫t2 − ∫((x +1)2 +1)2 = − |
|
t |
|
− |
∫ |
|
|
|
= |
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
|
((x +1)2 +1)2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
по формуле (1.13) запишем |
|
|
|
|
dx |
|
1 |
|
x |
|
|
|
|
dx |
|
1 |
|
|
x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
+ arctg x |
+ C |
|
|||||||
∫(x2 +1)2 |
2 |
|
|
|
|
|
∫ x2 +1 |
2 |
|
|
+1 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 +1 |
|
|
x |
2 |
|
|
|
|
||||||||||||||||||||||
= |
и применим полученную формулу ко второму слагаемому, |
взяв х +1 вместо х; |
= |
||||||||||||||||||||||||||||||||||
|
кроме того, |
в первом слагаемом вернемся к переменной х |
|
t |
|
= x2 |
+ 2x + 2 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
1 |
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
= − |
|
|
|
|
|
|
− |
|
|
|
|
|
+ arctg(x +1) |
+ C . |
|
|
|
|
||||||||||||||||||
|
|
2(x |
2 |
+ 2x + |
2) |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
(x +1) +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Окончательно
|
(3x + 2)dx |
|
|
|
3 |
|
|
|
|
|
x +1 |
1 |
|
∫ |
|
= − |
|
|
|
− |
|
− |
2 arctg(x +1)+ C = |
||||
(x2 + 2x + 2)2 |
2(x2 |
+ 2x + 2) |
2(x2 + 2x + 2) |
||||||||||
|
|
= − |
|
x + 4 |
|
|
− |
1 arctg(x +1)+ C . |
|||||
|
|
2(x2 + 2x + 2) |
|||||||||||
|
|
|
|
|
|
2 |
|
|
|||||
1.7. Разложение правильной рациональной дроби на простейшие дроби
Можно доказать, что любая правильная рациональная дробь представляется в виде суммы простейших дробей. Из теории, называемой алгеброй многочленов, известно, что любой многочлен ненулевой степени можно разложить на множители, соответствующие корням этого многочлена. Корни у многочлена могут быть либо действительными, либо комплексными.
Например, у |
многочлена f (x)= x3 +1 |
корни можно найти |
из уравнения |
|||||||||||||||||||
|
|
|
|
|
|
|
|
=1 ± |
|
|
= 1 ± |
|
|
|
|
|
|
i . |
||||
x3 +1 = 0 или |
(x +1)(x2 |
− x +1)= 0 , тогда |
x |
= −1, а |
x |
|
|
|
1 − 4 |
3 |
||||||||||||
2,3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
2 |
|
2 |
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Один корень |
x |
= −1 – действительное число, а два других |
|
x |
|
= 1 ± |
|
|
3 |
|
i – |
|||||||||||
|
2,3 |
|
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||
пара комплексно сопряженных чисел. Многочлен |
x3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
+1 раскладывается на |
|||||||||||||||||||||
три линейных |
множителя x3 +1 = (x − x )(x − x |
2 |
)(x − x |
). |
|
При |
|
этом |
||||||||||||||
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
произведение |
скобок, |
соответствующих |
паре |
комплексно-сопряженных |
||||||||||||||||||
корней, (x − x2 )(x − x3 ) равно квадратному трехчлену x2 − x +1,
коэффициенты которого – действительные числа. Аналогичное разложение на множители справедливо для любого многочлена Pn (x) степени n (n ≠ 0).
Такой многочлен имеет ровно n корней, причем комплексные корни всегда присутствуют парами, а именно парами комплексно-сопряженных чисел. Этот многочлен раскладывается на n линейных множителей:
Pn (x)= a0 (x − x1 )(x − x2 ) (x − x3 ),
где a0 – коэффициент многочлена при старшей степени x, т.е. при xn . Если в
28
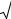
этом разложении перемножить пары скобок, соответствующие комплексносопряженным корням, и объединить одинаковые скобки, то разложение примет вид
Pn (x)= a0 (x −b1 )α1 (x −b)αk (x2 |
+ p1 x + q1 )β1 (x2 + ps x + qs )βs (1.14) |
здесь b1, …, bk – различные действительные корни многочлена, а квадратные трехчлены соответствуют различным парам комплексно-сопряженных корней. Показатели степени скобок называются кратностями корней.
Например, у многочлена пятой степени P5 (x)= 3(x − 2)2 (x + 4)(x2 + 6) есть различные корни: b1 = 2, кратности 2, b2 = –4, кратности 1 и пара комплексно
-сопряженных корней x3,4 = ± |
6 |
i кратности 1. |
F(x) |
|
|
||
Рассмотрим правильную рациональную дробь |
, где |
f (x) – |
|||||
f (x) |
|
||||||
|
|
|
|
|
|||
многочлен степени n. Пусть нам удалось разложить знаменатель f (x) на
множители по формуле (1.14). Тогда данная правильная дробь может быть представлена в виде суммы простейших дробей, знаменателями которых являются множители, на которые разложен знаменатель исходной рациональной дроби. В этой сумме могут быть представлены все возможные простейшие дроби, общий знаменатель которых равен знаменателю исходной дроби. Так, если в знаменателе исходной дроби есть множитель
(x − b)3 , то в разл ожении этой дроби на простейшие могут присутствовать три простейшие дроби типа I и II вида:
A1 |
, |
A2 |
, |
A2 |
, |
|
x − b |
(x − b)2 |
(x − b)3 |
||||
|
|
|
общий знаменатель которых (x − b)3 . Если в знам енателе исходной дроби
присутствует множитель (x2 + px + q)2 , то в разложении этой дроби на простейшие могут быть две простейшие дроби типа III и IV вида:
|
B1 x + C1 |
и |
B2 x + C2 |
, |
|
x2 + px + q |
(x2 + px + q)2 |
||
общий знаменатель которых равен (x2 |
+ px + q)2 . |
|
||
Теперь видно, что разложение правильной рациональной дроби на простейшие дроби выписать просто, если знаменатель разложен на множители в виде (1.14), при этом знаменатели этих простейших дробей нам известны, а о числителях нам известен лишь их вид (либо число, либо линейная функция). Например,
x2 |
|
A |
|
B |
|
Cx + D |
|
|
= |
|
+ |
|
+ |
|
. |
(x +1)(x − 2)(x2 + 3x +10) |
x +1 |
x − 2 |
x2 + 3x +10 |
||||
Здесь каждому множителю знаменателя соответствует одна простейшая
29

дробь, т.к. все корни знаменателя имеют кратность 1. В полученном разложении нам неизвестны коэффициенты A, B, C, D. Метод представления неизвестных коэффициентов буквами, с последующим определением их значений, называется методом неопределенных коэффициентов.
Итак, пусть правильная рациональная дробь представлена в виде суммы простейших дробей с неопределенными коэффициентами в числителях. Для отыскания значений коэффициентов приведем записанную сумму дробей к общему знаменателю – получим рациональную дробь с таким же знаменателем, как у исходной дроби. Мы хотим, чтобы полученная дробь тождественно совпала с исходной, поэтому подберем неопределенные коэффициенты так, чтобы у полученной и исходной дробей тождественно совпали числители. Тождественное равенство числителей – это тождественное равенство двух многочленов. Справедливы два критерия тождественного равенства двух многочленов.
Теорема 1.2. Для того чтобы два многочлена тождественно совпадали, необходимо и достаточно, чтобы у них совпадали коэффициенты при одинаковых степенях переменной.
Теорема 1.3. Для того чтобы два многочлена степени не выше n тождественно совпадали, необходимо и достаточно, чтобы совпадали их значения при (n + 1) различных значениях переменной.
Вернемся к отысканию значений неопределенных коэффициентов. Покажем на примере, как для их отыскания используются теоремы 1.2 и 1.3.
Пример 1.31. Разложить на простейшие дроби правильную дробь
x2 + 3 . x3 + 5x2 +10x
Разложим сначала знаменатель на множители: x3 + 5x2 +10x = x(x2 + 5x +10).
Квадратный трехчлен x2 |
+ 5x +10 не имеет действительных корней, т.к. его |
||||
дискриминант D = 25 – 4 · 10 · 1 = – 15 < 0. Имеем |
|||||
|
|
x2 + 3 |
x2 + 3 |
||
|
|
|
= |
|
. |
|
x3 |
+ 5x2 +10x |
x(x2 + 5x +10) |
||
Эта дробь представляется в виде суммы двух простейших дробей:
|
|
x2 + 3 |
= |
A |
+ |
Bx + C |
. |
|
|
||
|
|
x(x2 + 5x +10) |
|
x2 + 5x +10 |
|
||||||
|
|
|
x |
|
|
|
|||||
Приводя правую часть равенства к общему знаменателю, получим |
|||||||||||
|
x2 + 3 |
= |
A(x2 + 5x +10) + (Bx + C)x |
. |
(1.15) |
||||||
|
x(x2 + 5x +10) |
|
|
x(x2 |
+ 5x +10) |
|
|
|
|||
Уравняем числители этих дробей: |
|
|
|
|
|
|
|
||||
|
x2 + 3 = A(x2 + 5x +10) + (Bx + C)x . |
|
|||||||||
Для отыскания неизвестных |
коэффициентов A, B, C |
воспользуемся, |
|||||||||
30

например, теоремой 1.2. Раскроем скобки и приведем подобные в правой части равенства:
x2 |
+ 3 = (A + B)x2 |
+ (5A + C)x +10A. |
(1.16) |
|
Приравняем коэффициенты в левой |
и правой частях равенства |
при x2 |
||
(1 = A + B ), при x (0 = |
5A + C) |
и свободные члены (3 = 10 A). Получим |
||
систему трех линейных уравнений с тремя неизвестными: |
|
|||
|
A + B =1, |
|
||
|
|
|
|
|
|
5A + C = 0, |
|
||
|
|
10A = 3. |
|
|
|
|
|
||
Решение системы: A =103 , B =107 , C = −32 . Так как при найденных значениях
A, B, C коэффициенты при одинаковых степенях x в равенстве (1.16) совпадают, то из теоремы 1.2 следует, что числители левой и правой частей равенства (1.15) тождественно совпадают и, значит,
|
|
|
|
|
|
3 |
|
|
|
7 |
x |
3 |
|
|
|
|
|||
|
|
x2 + 3 |
|
|
|
|
|
|
|
|
− |
|
|
. |
|
||||
|
|
|
= 10 |
+ |
|
|
10 |
2 |
|||||||||||
|
|
x(x2 + 5x +10) |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
x2 + 5x +10 |
|||||||||||||
Пример 1.32. Разложить дробь |
x2 |
+ 2 |
|
|
|
на простейшие. |
|||||||||||||
(x +1)3 (x − 2) |
|
||||||||||||||||||
Применим метод неопределенных коэффициентов: |
|||||||||||||||||||
|
x2 + 2 |
A |
|
|
|
A |
|
|
|
A |
|
|
B |
||||||
|
(x +1)3 (x − 2)= (x +1)3 |
+ (x +1)2 + x +1 |
+ x − 2 . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
Приводя правую часть к общему знаменателю и приравнивая числители левой и правой частей, имеем
x2 + 2 = A(x − 2)+ A1 (x +1)(x − 2)+ A2 (x +1)2 (x − 2)+ B(x +1)3
или, раскрывая скобки и приводя подобные, получим
x2 + 2 = x3 (A2 + B)+ x2 (A1 + 3B)+ x(A − A1 −3A2 + 3B)+ (− 2A − 2A1 − 2A2 + B).
Приравнивая коэффициенты при одинаковых степенях x, получим систему уравнений для определения коэффициентов:
|
0 = A2 + B, |
|
|
|
1 = A1 + 3B, |
|
|
|
|
||
|
0 = A − A1 − 3A2 + 3B, |
||
|
|||
2 = −2A − 2A |
− 2A |
+ B. |
|
|
1 |
2 |
|
31
Решая эту систему, найдем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A = −1, A = |
1 |
, A = − |
2 , |
B = 2 . |
|
|
|
||||||||
|
|
|
1 |
|
3 |
2 |
9 |
9 |
|
|
|
|||||
В результате получаем разложение |
|
|
|
|
|
|
|
|||||||||
|
x2 + 2 |
1 |
|
|
|
1 |
|
|
2 |
|
2 |
|
||||
|
|
= |
− |
|
|
+ |
|
|
|
|
− |
|
|
+ |
|
. |
|
(x +1)3 (x − 2) |
(x +1)3 |
|
|
3(x +1)2 |
|
9(x +1) |
9(x − 2) |
||||||||
Пример 1.33. Вычислить интеграл ∫ |
|
|
x2 + 2 |
|
dx . |
|
|
|
||||||||
(x +1)3 (x − 2) |
|
|
|
|||||||||||||
Разложим подынтегральную дробь на простейшие и применим метод неопределенных коэффициентов (см. пример 1.32). Получим
|
|
∫ |
|
x2 |
+ 2 |
|
dx = − ∫ |
|
dx |
|
|
|
|
1 |
∫ |
|
|
dx |
2 |
∫ |
dx |
|
|
2 |
∫ |
dx |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
|
= |
|
|
|||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
3 |
3 |
(x |
2 |
9 |
x +1 |
9 |
x − |
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
(x +1) (x − 2) |
|
|
|
(x +1) |
|
|
|
+1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 1 |
|
1 |
|
2 |
|
x + |
|
|
2 |
|
|
x − 2 |
|
|
+ C = − |
|
2x −1 |
|
|
|
2 |
|
x − 2 |
|
+ C . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
= |
|
|
− |
|
|
− 9 ln |
|
1 |
+ |
9 ln |
|
|
|
|
|
|
|
+ |
9 ln |
|
|
|
|
|||||||||||||||||||||
2 |
(x +1)2 |
|
3(x +1) |
|
|
|
6(x +1)2 |
x +1 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Пример 1.34. Вычислить интеграл ∫ |
|
|
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(x |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1)(x −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Разложим подынтегральную дробь на простейшие: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
Ax + B |
|
C |
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
(x2 +1)(x −1)2 = |
(x2 +1)+ |
|
|
|
|
+ |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
(x −1)2 |
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Приведем дроби к общему знаменателю и приравняем числители: x = (Ax + B)(x −1)2 + C(x2 +1)+ D(x −1)(x2 +1).
Раскрыв скобки и приведя подобные, получим
x = x3 (A + D)+x2 (B − 2A + C − D)+ x(A − 2B + D)+ (B + C − D).
Далее, приравнивая коэффициенты при одинаковых степенях x, будем иметь следующую систему уравнений:
|
A + D = 0, |
|
|
|
|
|
|
B − 2A + C − D = 0, |
|||
|
A − 2B + D =1, |
|
|
|
|
||
|
B + C − D = 0. |
|
|
|
|
||
Решая эту систему, находим |
|
|
|
A = 0, B = −1 , C = |
1 , |
D = 0 . |
|
|
2 |
2 |
|
32
Таким образом, |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x |
|
|
|
0 x |
− |
|
|
|
|
|
|
|
0 |
|
|
|
|
1 1 |
|
|
1 1 |
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||
(x2 +1)(x −1)2 |
= |
|
|
+ |
|
|
|
|
+ |
|
|
|
= − |
2 |
|
|
+ |
2 |
|
|
|||||||||||||||
x2 +1 |
|
(x −1)2 |
x −1 |
x2 +1 |
(x −1)2 |
||||||||||||||||||||||||||||||
Поэтому |
|
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
= − |
1 |
∫ |
|
dx |
|
|
1 |
∫ |
|
|
dx |
|
1 |
arctg x − |
|
1 |
|
+ C . |
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
+ |
|
|
|
|
|
= − |
|
|
|
|
|
||||||||||||||
(x |
2 |
+1)(x − |
|
2 |
(x |
2 |
+1) |
2 |
|
(x |
|
2 |
2 |
2(x −1) |
|||||||||||||||||||||
|
|
1) |
|
|
|
|
|
|
|
|
−1) |
|
|
|
|
|
|
|
|||||||||||||||||
Пример 1.35. Вычислить интеграл ∫ |
|
|
|
|
|
|
x + 4 |
|
|
|
|
dx . |
|
|
|
|
|
|
|
||||||||||||||||
x3 |
+ 6x2 +11x + 6 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Так как подынтегральная функция является правильной дробью, то ее следует представить в виде суммы простейших дробей. Для этого разложим знаменатель на множители, для чего найдем корни знаменателя. Легко видеть, что многочлен x3 + 6x2 +11x + 6 обращается в нуль при x = −1, поэтому он делится без остатка на x +1. Выполняя деление по правилу деления многочленов, получим
x3 + 6x2 +11x + 6 = (x +1)(x2 + 5x + 6)= (x +1)(x + 2)(x + 3).
Теперь |
|
|
|
|
|
|
|
|
|
|
|
x + 4 |
= |
A |
|
+ |
B |
+ |
C |
|
. |
|
x3 + 6x2 +11x + 6 |
x +1 |
x + 2 |
x + 3 |
||||||
|
|
|
|
|
||||||
Приводя дроби к общему знаменателю и приравнивая числители, получим
x + 4 = A(x + 2)(x + 3)+ B(x +1)(x + 2)+ C(x +1)(x + 2).
Для отыскания неизвестных коэффициентов применим теорему 1.3. Т.к. для тождественного равенства многочленов степени не выше двух
(см. многочлены в левой и правой частях равенства) достаточно
совпадения их значений в трех различных точках, т.е. при трех |
||||||||||||||||||||||||||||||||||||||
различных значениях |
x, то уравняем значения в левой и правой части в |
|||||||||||||||||||||||||||||||||||||
точках x = – 1, x |
= –2, x = – 3. Для этого подставим эти значения по очереди в |
|||||||||||||||||||||||||||||||||||||
правую и левую части последнего равенства. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Полагая x = −1, |
имеем 3 = 2A, |
т.е. A = |
3 . Если x = −2, то |
|
2 = −B , т.е. B = −2. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При x = −3 получим 1 = 2C , т.е. C = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x + 4 |
|
|
|
|
|
|
1,5 |
|
|
|
− 2 |
|
|
|
|
0,5 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
+ |
+ |
|
|
|
|
|
, |
|
|
|||||||||||||||||
откуда |
|
|
|
x3 + 6x2 +11x + 6 |
|
|
|
|
x +1 |
|
|
|
x + 2 |
|
|
|
|
x + 3 |
|
|
|
|
|
|||||||||||||||
|
|
|
x + 4 |
|
3 |
|
|
dx |
|
|
|
|
|
dx |
|
1 |
|
|
|
dx |
|
|
||||||||||||||||
∫ |
|
|
|
dx = |
∫ |
− |
2∫ |
+ |
∫ |
|
= |
|||||||||||||||||||||||||||
x |
3 |
+ 6x |
2 |
+11x + 6 |
2 |
x +1 |
x + 2 |
2 |
|
x + 3 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
= |
3 ln |
|
x +1 |
|
− 2ln |
|
x + 2 |
|
+ |
1 ln |
|
x + 3 |
|
+ C . |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
33
Пример 1.36. Вычислить интеграл ∫ |
|
|
x5 +1 |
dx . |
||
x |
4 |
−8x |
2 |
+16 |
||
|
|
|
|
|||
Обратите внимание на то, что под знаком интеграла стоит неправильная дробь. Следовательно, сначала необходимо выделить целую часть этой дроби. Разделив по правилу деления многочленов числитель на знаменатель, будем иметь
x5 +1 |
= x + |
8x3 −16x +1 |
= x + |
8x3 −16x +1 |
= x + |
8x2 −16x +1 |
. |
x4 −8x2 +16 |
x4 −8x2 +16 |
(x2 − 4)2 |
|
||||
|
|
|
(x − 2)2 (x + 2)2 |
||||
Разложим теперь полученную правильную дробь на простейшие:
8x2 −16x +1 |
= |
A |
|
B |
|
C |
|
D |
|
|
|
+ |
|
+ |
|
+ |
|
. |
|
(x − 2)2 (x + 2)2 |
(x − 2)2 |
x − 2 |
(x + 2)2 |
x + 2 |
|||||
Приводя дроби к общему знаменателю и приравнивая числители, получим
8x3 −16x +1 = A(x + 2)2 + B(x − 2)(x + 2)2 + C(x − 2)2 + D(x − 2)2 (x + 2).
Для отыскания неизвестных коэффициентов воспользуемся обеими
теоремами 1.2 и 1.3. Полагая x = 2, найдем 33 =16A, т.е. A = 33 ; при |
x = −2, |
||||||
|
|
|
|
31 ; если |
|
16 |
|
получим |
− 31 =16C , |
т.е. |
C = − |
x = 0, то |
1 = 4A −8B + 4C + 8D . |
||
|
|
|
|
16 |
|
|
|
Заменив A и C их значениями, получаем уравнение |
|
|
|||||
1 = 33 −8B − 31 + 8D , |
или |
−16B +16D =1. |
|
|
|||
4 |
4 |
|
|
|
|
|
|
Для того чтобы найти B и D, составим еще одно уравнение. Уравняем |
|||||||
коэффициенты при x3 , получим 8 = B + D . Решив систему уравнений |
|
||||||
|
|
|
|
B + D =8, |
|
|
|
|
|
|
|
16B +16D =1, |
|
|
|
|
|
|
− |
|
|
||
находим D =12932 , B =12732 . Окончательно получаем
|
|
x |
5 |
+ |
1 |
|
|
|
|
|
33 |
|
|
+ |
|
127 |
|
− |
|
31 |
|
|
|
+ 129 |
|
|
||||||||
|
|
|
|
dx = x + |
|
|
|
|
|
|
|
|
|
|
dx = |
|||||||||||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
−8x |
|
+16 |
|
|
|
16(x |
− 2) |
|
32(x − 2) |
|
16(x + 2) |
|
32(x + |
2) |
||||||||||||||||||
|
|
|
|
|
|
|
x2 |
33 |
|
|
127 |
ln |
|
x − 2 |
|
31 |
|
|
|
129 |
ln |
|
x + 2 |
|
+ C . |
|
|
|||||||
|
|
|
|
= |
|
|
− |
|
|
+ |
|
|
+ |
|
|
+ |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
16(x − 2) |
32 |
16(x + 2) |
32 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
34
