Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

Воронежский государственный архитектурно-строительный университет

А.М. Дементьева, С.В. Артыщенко, В.А. Попова

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Учебное пособие

Рекомендовано редакционно-издательским советом Воронежского архитектурно-строительного университета

в качестве учебного пособия для студентов заочной формы обучения всех специальностей

Воронеж 2010

1

ВВЕДЕНИЕ

Пособие по интегральному исчислению предназначено для студентов заочной формы обучения, но, безусловно, может быть использовано и студентами дневной формы всех специальностей ВГАСУ.

Без интегралов не может обойтись ни физика, ни химия, ни теоретическая механика, ни строительная механика и т.д. и т.п., а значит, практически все инженерные дисциплины.

Вэтом пособии рассмотрены почти все виды используемых на практике интегралов: определенных, двойных, тройных и криволинейных. Для их вычисления нужно уметь находит неопределенные интегралы – им посвящена первая глава. В этой главе рассмотрены методы интегрирования, решено большое количество примеров; при этом авторы старались объяснить идеи выбора применения того или иного метода. Первая глава самая трудная, постарайтесь разобраться во всех нюансах решения разобранных примеров.

Разобравшись в неопределенных интегралах, можно приступить к изучению остальных глав, в которых подробно рассмотрены задачи, порождающие определенные, двойные, криволинейные интегралы и т.д. Идеи решения таких задач похожи, с помощью этих идей обобщаются формулы вычисления различных величин. Все эти формулы получаются применением предельного перехода, причем очень естественно.

Авторы настоятельно советуют внимательно читать и разбирать теоретические вопросы, прежде чем использовать полученные формулы для вычисления интегралов (их использование достаточно простое для читателя, освоившего первую главу).

Во второй и третьей главах подробно разобрано множество примеров и задач, объясняется выбор формулы при решении каждой задачи.

Авторы надеются, что данное пособие поможет читателям в освоении материала – сложного и очень важного для дальнейшего обучения.

1.НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1.1.Первообразная и неопределенный интеграл

Вдифференциальном исчислении по функции f(x) строилась другая функция f ´(x), называемая производной функции f(x). В интегральном исчислении одна из задач – по известной производной некоторой функции отыскать эту функцию. Иными словами, рассматривается задача, обратная задаче дифференцирования.

Определение 1.1. Функция F(x) называется первообразной функции

f(x) на некотором промежутке, если во всех точках этого промежутка выполняется равенство F′(x) = f(x).

Пример 1.1. Найти первообразную от функции f(x) = x2.

3

первообразная, то эта первообразная не является единственной. Так, в предыдущем примере можно было взять в качестве первообразных функций

исчерпываются все первообразные от функции x2. Это вытекает из следующей теоремы.

при любом значении x на отрезке [a, b].

Обозначим: F1(x) ─ F2(x) = φ(x). Тогда на основании равенств (1.1)

при любом значении x на отрезке [a,b], откуда следует, что на отрезке [a,b] φ(x) есть постоянная. Чтобы убедиться в этом, вспомним теорему Лагранжа.

Теорема Лагранжа. Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a, b] найдется, по крайней мере, одна точка с, a < c < b, что

f (b) − f (a) = f ′(c)(b − a) .

Вспомним, что любая дифференцируемая функция непрерывна, поэтому первообразные F1(x) и F2(x) от функции f(x) и функции

ϕ(x) = F1 (x) − F2 (x) удовлетворяют условию теоремы Лагранжа на отрезке

4

[a, b]. Какова бы ни была точка x [a, b], в силу теоремы Лагранжа

ϕ(x) −ϕ(a) =ϕ′(ξ)(x − a) ,

где a < ξ < x. Из (1.2) φ´(ξ) = 0, т.е. φ(х) – φ(a) = 0 или ϕ(x) =ϕ(a) .

Таким образом, функция φ(x) в любой точке x отрезка [a, b] сохраняет значение φ(a), т.е. функция φ(x) является постоянной на отрезке [a, b].

Из доказанной теоремы следует, что если для данной функции f(x) на некотором отрезке найдена какая-нибудь одна первообразная F(x), то на этом отрезке любая другая первообразная f(x) имеет вид F(x)+С, где С = const.

Определение 1.2. Если функция F(x) является первообразной для функции f(x), то выражение F(x) + С называется неопределенным интегралом

от функции f(x) и обозначается символом ∫ f (x) dx. Иными словами,

Функцию f(x) называют подынтегральной функцией, f(x)dx – подынтегральным выражением, знак ∫ − знаком интеграла, х - переменной интегрирования.

Заметим, что неопределенный интеграл – это семейство функций, отличающихся в каждом промежутке области определения на постоянную. Исходя из этого два неопределенных интеграла будем считать равными, если производные от этих интегралов совпадают.

Нахождение первообразной для данной функции f(x) называется

интегрированием функции f(x).

Свойства неопределенного интеграла

Свойство 1.1. Производная от неопределенного интеграла равна подынтегральной функции:

(учитываем определение дифференциала функции и формулу (1.4)). Из последнего свойства и формулы (1.3) следует, что подынтегральное выражение равно d(F(x) + C) = dF(x).

5

Свойство 1.3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной

∫dF(x)= F(x) + C .

Из формул в свойствах 1.2 и 1.3 видно, что знаки интеграла и дифференциала, взятые в любом порядке, «взаимно уничтожают» друг друга.

Свойство 1.4. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме интегралов от этих функций:

Для доказательства достаточно найти производную правой части этого равенства. Учитывая свойство 1.1, имеем

(∫ f1 (x)dx +∫ f2 (x)dx)′ = (∫ f1 (x)dx)′ + (∫ f2 (x)dx)′ = f1 (x) + f2 (x).

Так как производная правой части равенства (1.6) равна подынтегральной функции неопределенного интеграла, стоящего в левой части равенства (1.6), то (1.6) справедливо.

Свойство 1.5. Постоянный множитель можно выносить за знак интеграла, т.е. если a = const ≠ 0, то

Для доказательства равенства (1.7) найдем производные от левой и правой частей:

(∫a f (x)dx)′ = a f (x), (a∫ f (x)dx)′ = a(∫ f (x)dx)′ = a f (x).

Производные от правой и левой частей равны, следовательно, (1.7) верно.

1.2. Таблица интегралов

Непосредственно из определения 1.2 и таблицы производных вытекает таблица интегралов:

6

Заметим, что формулы 7, 8, 11′, 12, 13′, 14 таблицы интегралов не видны непосредственно из таблицы производных. Их можно проверить дифференцированием, а можно получить, используя методы интегрирования. Например, для формулы 7 имеем

следовательно, формула 12 верна.

Пример 1.2. Найти неопределенный интеграл ∫(2x3 − 3sin x + 5x )dx .

Воспользовавшись свойствами 1.4 и 1.5 и формулами 1 и 3 таблицы интегралов, получим

7

Пример 1.3.

Преобразуем, если удастся, подынтегральную функцию в сумму функций, от которых можно найти интегралы с помощью таблицы интегралов. Для этого разделим числитель дроби на знаменатель почленно,

т.е. 3xx+5 = 3xx + 5x = 3 + 5x . Теперь

формулы 1 и 2 таблицы интегралов.

Пример 1.5. Найти неопределенный интеграл ∫4xx22 ++15dx .

В таблице интегралов есть лишь ∫ x2dx+1 = arctgx + C . Поэтому преобразуем подынтегральное выражение почленным делением числителя на

запишем числитель так, чтобы при почленном делении часть числителя разделилась бы на знаменатель нацело, а вторая часть была бы константой. Получим

применения приходится иногда сначала преобразовывать подынтегральную функцию, используя приемы алгебры, тригонометрии и др.

8

1.3. Интегрирование методом подстановки или замены переменной

Пусть требуется найти интеграл ∫ f (x) dx, причем представить его в

виде суммы табличных интегралов не удается.

Воспользуемся свойством 1.3 неопределенного интеграла о том, что подынтегральное выражение – это дифференциал искомой первообразной. Известно, что дифференциал функции не меняет своего вида от того, является ли аргумент функции независимой переменной или функцией от другой переменной. Поэтому если

∫ f (x)dx = F(x)+ C ,

то f(x)dx = dF(x) и это равенство справедливо и если х независимая переменная, и если х – функция. Иными словами,

f(t)dt = dF(t) (x = t); f(φ(t))dϕ(t) = dF(φ(t)) (x = φ(t)); f(g(x))dg(x) = dF(g(x)) (t = g(x)) и т.д.

∫ f (g(x))dg(x)= F(g(x))+ C .

Вышесказанное дает возможность использовать формулы таблицы интегралов как тождественные равенства, подставляя в них вместо х любые дифференцируемые функции. Например, по формуле 9 таблицы интегралов

известно, что ∫ex dx = ex + C . Поэтому ∫ex2 dx2 = ex2 + C , ∫esin x d sin x = esin x + C

и т.д. Конечно, в подынтегральном выражении обычно присутствует dx , а не dg(x), но можно самим создать дифференциал от некоторой функции, которой мы хотим отвести далее роль переменной интегрирования. Например, докажем формулу 7 из таблицы интегралов, т.е. найдем

∫tgxdx = ∫cossin xx dx . Поскольку sin x – это «почти» производная от cos x ((cos

x)' = – sin x), то попробуем преобразовать подынтегральное выражение, подводя cos x под знак дифференциала. Т.к. df(x) = f ' (x) dx, то

d(cos x) = – sin x dx, откуда sin x dx = – d(cos x). Перепишем искомый интеграл в виде

9

Сравним полученный интеграл с табличным ∫1x dx = ln x + C , – искомый получится из него, если вместо x подставить cos x, т.е.

∫cos1 x d cos x = ln cos x + C . Используя последнее равенство, имеем

∫tgxdx = −ln cos x + C .

Выведем для примера табличную формулу 11', которая в частном случае (a = 1) совпадает с формулой 11.

подынтегральное выражение, по которому нельзя сразу воспользоваться табличной формулой, а нужно сделать еще какие-то преобразования. Кроме того, присутствие функции g(x) вместо переменной интегрирования тоже

создает дополнительные трудности. Поэтому функцию g(x) обозначают другой буквой, например g(x)=t , и в подынтегральном выражении заменяют

В этом примере мы без труда перешли к новой переменной интегрирования, т.к. подынтегральное выражение «легко» выражалось через t = sin x . Конечно, так происходит не всегда.

Рассмотрим, например, ∫ xx+−52 dx . Попробуем найти этот интеграл,

взяв за новую переменную знаменатель дроби, т.е. обозначив t = x − 2 .

10

=23 (x − 2)3 +14x − 2 + C .

Вэтом примере видно, что без введенного обозначения было бы трудно

увидеть, как подынтегральное выражение выражается через функцию

x − 2 . Заметим, что проведенные выше преобразования удалось осуществить, т.к. старая переменная x легко и однозначно выражалась через новую переменную t. Фактически, придумав, какую функцию g(x) мы

возьмем в качестве новой переменой t, мы подставили затем в интеграл вместо x функцию φ(t), получив ее из равенства 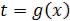, выразив x через t. В некоторых случаях новую переменную вводят, заменив x на функцию от новой переменной t с целью упростить подынтегральное выражение.

Рассмотрим, например, ∫1 − x2 dx . В таблице интегралов нет интеграла от

корня из квадратного трехчлена. Заменим x такой функцией, чтобы этот корень извлекся, т.е. избавимся от иррациональности. Заменим, например, x тригонометрической функцией x = sint (t=arcsinx). Тогда

Переход от старой переменной к новой называют методом подстановки или замены переменной. Корректнее описанную выше процедуру можно сформулировать так:

если x = φ(t) – непрерывно дифференцируемая функция, имеющая обратную, то

11