Задачи и упражнения для организации самостоятельной работы по курсам «Математика», «Спецглавы математики». Катрахова А.А., Васильев Е.М

ЗАНЯТИЕ № 68

ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ

Литература: [18], c.198-159, [20], с.44 -140, [31] c. 282-293

Контрольные вопросы и задания

1.В чем заключается графа и их свойства?

2.Какие вы знаете операции над графами ?

3.В чем заключается матричное представления графа?

4.Как определенются сильные компоненты графа ?

5.Как вычисляются метрические характеристики графа?

Дополнительные вопросы

1.Как применяются графы при решении тезнических задач (привести пример).?

2.В чем заключается метод построения матриц достижимости, сильной связности графа ?

Примеры решения задач

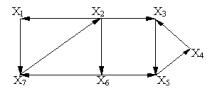
Задача 1. Определить метрические характеристики графа рис. 16

Рис. 16

Решение. Метрические характеристики определяются следующим образом:

81

Радиус графа равен 1, диаметр равен 2. Центр графа - вершина x2; Медиана графа - вершина x2.

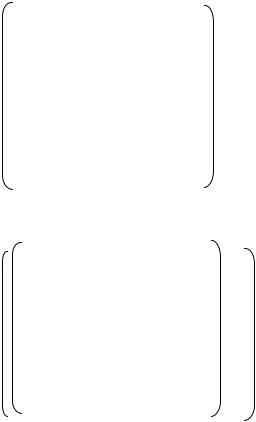
Задача 2.

Найти сильные компоненты графа рис. 17

Рис. 17

Решение. Для данного графа матрицы R, Q и S имеют вид:

82

В соответствии с матрицей S сильные компоненты графа: х1, х2, х6,х7 –первая сильная компонента; х3, х4, х5 - вторая сильная компонента.

Задачи и упражнения для самостоятельного решения

Определить сильные компоненты графов. изображенных на рис.18 а, б, в, г,д,е,ж,з .

83

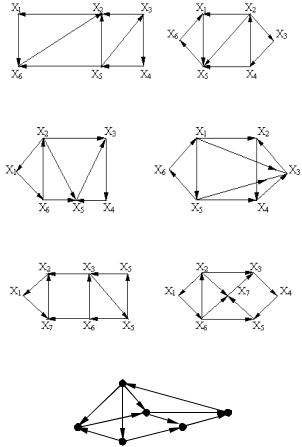
аб

де

жз

Рис. 18

1.Доказать, что в неорграфе число вершин с нечетной степенью четно.

2.Построить граф (если он существует) с последователь-

ностью степеней а) (4,3,3,2,2); б) (5,4,2,2,1) .

3.Найти матрицы достижимости и контрдостижимости для графов G1 ,G2, G4, изображенных на рис. и .

84

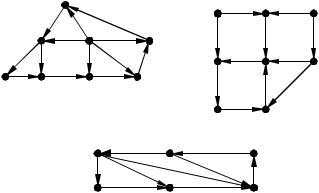
4. Доказать, что если G несвязный граф, то G связ-

ный.

5.Доказать, что в любом графе каждая его база содержит все вершины, имеющие нулевые полустепени захода.

6.Для графов, изображенных на рис.19, найти сильнее компоненты, построить конденсацию, найти базы и антибазы.

Рис. 19

8.Доказать, что хроматическое число каждого n-

вершинного дерева (n 2) равно 2.

Форма отчетности: устный опрос

85

ЗАКЛЮЧЕНИЕ

Настоящее пособие написано авторами на основе многолетнего опыта преподавания курса высшей математики в техническом университете и рассчитано на студентов тех специальностей, в программу которых входят курсы «Математика», «Спецглавы математики».

Материал пособия авторы постарались изложить так, чтобы максимально помочь студентам в их самостоятельной работе. С этой целью в пособии разобрано большое количество примеров, которые помогут студентам глубже усвоить

теоретический материал курса и приобрести навыки решения задач.

86

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Гмурман В.Е. Теория вероятностей и математическая статистика / В. Е. Гмурман. М.: Высш.шк., 1972.

2.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике /В. Е. Гмур-

ман. М.: Высш.шк., 1979.

3.Теория автоматического управления Под ред. В. Б. Яковлева. М.: Высш.шк., 2003.

4.Теория автоматического управления: Ч.1. / Под ред. А. А. Воронова. М. Высш.шк., 1986

5.Пискунов Н.С. Дифференциальное и интегральное исчисления: Ч.2. / Н. С. Пискунов. М.: Интеграл-Пресс, 2003

6.Мак-Кракен Д. Численные методы и программирование на Фортране /Д. Мак-Кракен, У. Дорн. М.: Мир, 1977.

7.Волков И.К. Исследование операций /И. К. Волков, Е. А. Загоруйко. М.: МГТУ им. Н.Э. Баумана, 2000.

8.Вентцель Е.С. Исследование операций / Е. С. Вентцель. М.: Дрофа, 2004.

9.Кузин Л.Т. Основы кибернетики: Ч.2. /Л. Т. Кузин. М.: Энергия, 1979.

10.Горелик А.Л. Методы распознания /А .Л. Горелик, В. А. Скрипкин. М.: Высш.шк., 1989.

11.Теория автоматического управления /под ред. А. А. Воронова. М.:Высш.шк., 1986.Ч.2.

12.Кошляков Н. С. Уравнения в частных производных математической физики / Н. С. Кошляков, Э. Б. Глинер, М. М. Смирнов. М.: Высш. шк. 1970.

13.Семенов М.П. Методы математической физики: Пособие / М. П. Семенов.Воронеж: ВГТУ. 2002.

14.Смирнов М.М. Задачи по уравнениям математи-

ческой физики / М. М. Смирнов. – М.: Наука, 1975. – 127 с.

87

15.Лаврентьев М.А., Люстерник Л.А. Курс вариацион ного исчисления / М.А. Лаврентьев, Л.А. Люстерник. М.: Гостехиздат, 1950.

16.Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление / Л.Э. Эльсгольц. -М.: Наука, 1969.

17.Краснов М.Л. Вариационное исчисление./ М.Л. Краснов, Г.И. Макаренко, А.И. Киселев. – М.: Наука, 1973. - 188 c.

18.Судоплатов С.В. Элементы дискретной математики: учебник / С.В. Судоплатов, Е.В. Овчинникова. М.: ИНФРА-М, 2002. – 280 с.

19.Леденева Т.М. Специальные главы математики.

Дискретная математика: учеб. пособие / Т.М. Леденева. Воро-

неж: ВГТУ, 1997. – 130 с.

20. Собенина О.В. Дискретная математика: учеб. пособие / О.В. Собенина. Воронеж: ВГТУ, 2012. – 200 с.

21.Тишин В.В. Дискретная математика в примерах и задачах / В.В. Тишин. СПб.: БХВ-Петербург. 2008. – 352 с.

22.Гаврилов Г.П. Задачи и упражнения по дискретной математике: учеб. пособие / Г.П. Гаврилов, А.А. Сапоженко. – 3-е изд., перераб. М.: ФИЗМАТЛИТ, 2005. – 416 с.

23.Булгакова И.Н. Дискретная математика. Элементы теории. Задачи и упражнения. Часть 1: учеб. пособие / И.Н. Булгакова, Г.Ф. Федотенко. Воронеж: ВГУ, 2004. – 61 с.

24.Кузнецов О.П. Дискретная математика для инже-

нера / О.П. Кузнецов. СП.: Лань, 2005. - 400 с.

25. Катрахова А.А. Теория вероятностей и элементы математической статистики: учеб. пособие / А.А Катрахова, В.С. Купцов, А.В. Купцов. Воронеж: ВГТУ, 2009.

88

26.Катрахова А.А. Элементы уравнений математической физики: учеб. пособие / А.А Катрахова Г.Ф. Федотенко, В.С. Купцов, А.В. Купцов. Воронеж: ВГТУ, 2012.

27.Катрахова А.А. Элементы вариационного исчисления и приложение к теории управления : учеб. пособие / А.А Катрахова., Е.М. Васильев, В.С. Купцов, А.В. Купцов. Воронеж: ВГТУ, 2012.

28.Катрахова А.А. Дискретная математика в задачах управления : учеб. пособие / А.А Катрахова., Е.М. Васильев, В.С. Купцов, Воронеж, 2016. -144 с.

29.Катрахова А.А. Спецглавы математики: Ч.1 : учеб. пособие / А.А Катрахова, В.С. Купцов. Воронеж, / 2017.

30.Краснов В.Л. Вариационное исчисление / М. Л. Краснов, Г. И. Макаренко, А. И. Киселев. Москва: Наука, 1973, -190 с.

31.Жуков В.М. Практические занятия по математике Ростов на Дону: Феникс, 2012 – 343 с.

32.Асеев Г.Г. Дискретная математика: учеб. пособие / Г. Г. Ассев, О. М. Абрамов, Д. Э. Ситников. Ростов на Дону: Фе-

никс, 2003 – 144 с.

89

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ……………………………………………………..….3

Занятие № 49. Вычисление вероятностей в классической схеме с использованием формул комбинаторики. Геометрические вероятности……………………………………………………………....3 Занятие № 50. Теоремы сложения и умножения вероятностей…..6 Занятие № 51. Формула Байеса……………………………..……....9 Занятие № 52. Числовые характеристики распределений Пуассона, биноминального, равномерного, нормального и показательного……………………………………………………………….……12

Занятие № 53. Система двух случайных величин …...…………..19 Занятие № 54. Доверительный интервал……..………………......21 Занятие № 55. Статистические оценки параметров распределения…………………………………………………………………...23 Занятие № 56. Методы расчета свободных характеристик выборки…………………………………………………………………….27

Занятие № 57. Статистическая проверка статистических гипотез………………………………………………………………...….29

Занятие № 58-61. Решение уравнений математической физики……………………………………………………………….……31

Занятие № 62. Элементы вариационного исчисления……….56

Занятие № 63-64. Теория множеств. Комбинаторика……..........66 Занятие № 65-67. Основы математической логики. Булевы функции…………………………………………………………………..76 Занятие № 68. Элементы теории графов...………………………81

ЗАКЛЮЧЕНИЕ…………………………………………………….86

БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………..……87

90