Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1966

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 163 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

	b	a	z	a	или	b-a	=	b-z	(2.1.3)
	z	a	b	z		b-z		z-a

Золотое сечение отрезка [a,b] производят две точки:

c	a	(1	)(b	a)
					(2.1.4)
					(2.1.4)
d	a	(b	a),	=0.5(1- 5) 0.618,

При этом, точка с производит золотое сечение отрезка [a,d], а точка d - золотое сечение отрезка [c,b].

Вычислим f(с) и f(d). Если f(с)<f(d), то отбрасываем интервал

]d,b[ и полагаем
a1 = a, b1		d , d1 c, c1	a1	(1			)(b1	a1 ).
Если f (c)	f (d), то полагаем
a	c, b = b, c = d, d = a				1	+ (b -a			).
1	1	1	1		1		1	1

Таким образом, на каждом следующем шаге метода золотого сечения требуется вычислить лишь одно значение унимодальной функции.

Приведем план организации вычислений при поиске точки минимума x* функции f методом золотого сечения с абсолютной

погрешностью .

Вычислить с и d по формулам (2.1.4).

Вычислить e

f (c)

f (d). Если e <0, перейти к п.5; если

e =0, перейти к п.7; если e >0, перейти к п.3.

Положить а=с и вычислить h

, при этом если

, то x*

fmin f(x*).

Положить c=d и вычислить d по (2.1.4). Перейти к п.2.

Положить b=d и вычислить h

. Если h

, то

a b

fmin

f(x*).

Положить d=c и вычислить с по (2.1.4). Перейти к п.2.

Положить a=c, b=d и вычислить h

b a

. Если h

то положить x*	a b	, fmin f(x*); в противном случае
	2

перейти к п.2.

Если количество вычислений n функции f задано, то оптимальной стратегией поиска минимума является метод Фибоначчи. Этот метод связан с последовательностью чисел Фибоначчи {Fk}, определяемой соотношениями

Fk 2 Fk Fk 1 ,

F1 F2 1

Первые четырнадцать членов этой последовательности

имеют вид:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.

Приведем план поиска на отрезке [a,b] точки х*, минимизирующей функцию f, основанный на использовании чисел Фибоначчи. Количество вычислений значения функции задано и равно n.

1.Сравнить 1 и n:

а) если n=1, перейти к п.2; б) если n>1, перейти к п.3.

Вычислить x*

fmin

f(x*). Конец.

Вычислить

x a

a), x

=a+

Fn+1

(b-a)

(2.1.5)

Fn+2

4.Вычислить f(x1), f(x2).

5.Сравнить 2 и n:

а) если n=2, перейти к п.6; б) если n>2, перейти к п.9.

6.Сравнить f(x1) и f(x2):

а) если f (x1 ) f (x2 ), перейти к п.7; б) если f (x1 ) f (x2 ), перейти к п.8.

7. Положить	x*	x1	, fmin	f (x1 ). Конец.
8. Положить	x*	x2	, fmin	f (x2 ). Конец.

9.Сравнить f(x1) и f(x2):

а) если f (x1 ) f (x2 ), перейти к п.10;

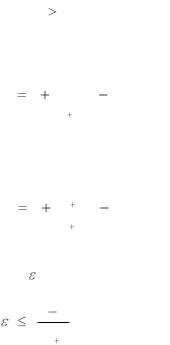
б) если f (x1 ) f (x2 ), перейти к п.13.

10. Произвести следующие переобозначения:

x2 = b, x1 = x2, n-1 = n.

11. Вычислить:

x a	Fn		(b a).	(2.1.6)
x a			(b a).	(2.1.6)
1	Fn
	Fn	2

12.Вычислить f(x1) и перейти к п.6.

13.Произвести следующие переобозначения

x1 = a, x2 = x1, n-1 = n.

14. Вычислить:

x	a		Fn 1	(b a).	(2.1.7)

2			Fn 2

15. Вычислить f(x2) и перейти к п.6.
Погрешность		найденного по методу Фибоначчи значения

х*, минимизирующего функцию f, имеет оценку:

b a . Fn 2

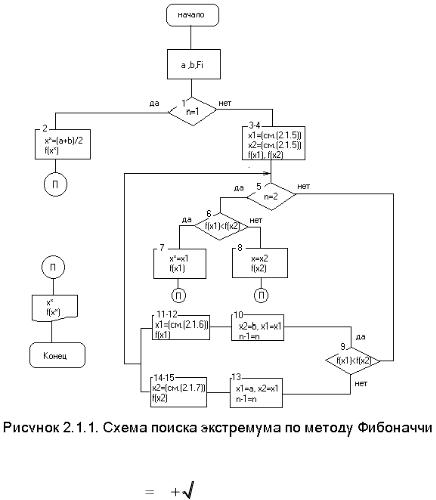
Для большей наглядности метода Фибоначчи приведем блоксхему вычислений (рис. 2.1.1).

Пример. Определить минимум функции

	1
f (x)	1	x

	x
	x
на отрезке[1,2] с помощью шести вычислений функции.
Решение будем искать с помощью методов дихотомии и
золотого сечения:

а) Метод дихотомии Полученные в процессе вычислений значения переменных

удобно записывать в виде таблицы:

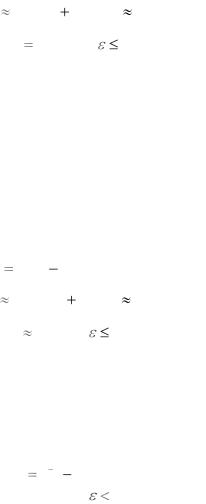
a	b	δ	c	d	f(с)	f(d)	h
1	2	0.1	1.45	1.55	1.8938	1.890	0.275
1.45	2	0.1	1.675	1.775	1.891	1.896	0.1625
1.45	1.775	0.01	1.6075	1.6175	1.8899	1.890	0.084

1.451.6175

		x*	1		(1.45	1.6175)		1.534,
	Ответ:	x*	2		(1.45	1.6175)		1.534,
	Ответ:		2
		f (x*)			1.89034,			0.084.
	б) Метод золотого сечения
a	b	c			d		f(с)		f(d)	e	h
1	2	1.382			1.618		1.89918		1.89005	e<0	0.309
1	1.618	1.236			1.382		1.90208		1.8992	e>0	0.191
1.236	1.618	1.382			1.472		1.8992		1.8926	e>0	0.118
1.382	1.618	1.472			1.528		1.8926		1.8906	e>0	0.073
1.472	1.618	1.528			1.5623		1.8906		1.88999	e>0	0.045
1.528	1.618
	Здесь e вычисляется по формуле
		e	f (c) f (d)
		x*	1	(1.528		1.618)		1.573,
	Ответ:	x*	2	(1.528		1.618)		1.573,
	Ответ:		2
		f (x*)			1.8899,		0.045.

Указанные задачи решить любым из рассмотренных методов.

Задачи для самостоятельного решения

2.1.1. Определить минимальное значение функции: f (x) e x 2 cos x

на отрезке[0;1] с погрешностью

0.05.

2.1.2. Вычислить наименьшее значение функции f на отрезке, точку х* определить с точностью до 0,05:

а) f(x)=xsinx+2cosx,

[

];

б)

f(x)=

1+x2 +e-2x ,

[0;1];

в)

f(x)=10x lg

[0,5;1];

г)

f(x)=

x(ln x 1),

[0,5;1];

д)

f(x)=

2x -2x2 ,

[3,5;4,5].

ln 2

2.1.3. Вычислить максимальное значение функции f на отрезке, точку х* определить с точностью до 0,01:

а)

f(x)=1+x-

[0;1];

б) f(x)=2x2 -(x+1)4 ,

[-3;-2];

в) f(x)=

-e

-2x,

[-1,5;1];

г) f(x)=x-

+cosx,

[0;1];

д) f(x)=1-6x-3x2 -x6 ,

[-1;0];

е) f(x)=20x-x2 +8x4 ,

[3;3,5].

2.1.4. Проверить соотношение между числами Фибоначчи Fn

и величиной

(уравнение Люкаса)

(

для n=0, 1, 2. Установить ошибку аппроксимации

2.1.5. Найти минимум функции

4x2

на отрезке [0;1] при четырех экспериментах. Эксперименты должны отстоять друг от друга по меньшей мере на 0,05.

Какова длина последнего интервала неопределенности? Какое наибольшее значение при этом достигается?

2.2.Методы полиномиальной интерполяции

2.2.1.Интерполирующий полином и его свойства

Пусть после проведения k испытаний имеет место следующая ситуация:

ak < xk < bk ; f(ak) > f (xk) < f(bk),

которая в силу унимодальности функции f(x) гарантирует, что точка минимума x* будет находиться внутри интервала [ak. bk], т. е.

ak < x* < bk.

Совокупность таких точек (ak, xk, bk) будем называть совокупностью “удачных точек”.

Рассмотрим класс методов, называемых методами полиномиальной интерполяции, основная идея которых заключается в следующем: по информации об m испытаниях {xi, f(xi),

i = 1,2,…,m} строится интерполирующий полином φn(x) степени n ≤ m-1, обладающий следующими свойствами:

• φn(x) – равномерное приближение минимизируемой

функции на интервале [ak, bk];

• точка минимума x полинома φn(x) определяется достаточно просто.

Отмеченные свойства полинома φn(x) позволяют на каждом шаге поиска использовать для сокращения текущего интервала неопределенности не только информацию о точках испытаний xi, но и информацию о значениях функции f(xi) в этих точках.

2.2.2 Квадратичная интерполяция

Метод квадратичной интерполяции часто называют методом Пауэлла. Сущность этого метода заключается в следующем: по трем

точкам функция f(x) аппроксимируется квадратичной параболой φ2(x) (интерполяционным многочленом Лагранжа), после чего находится точка минимума полинома φ2(x). Затем положение минимума функции f(x) аппроксимируется положением минимума полинома φ2(x), так как его проще вычислить.

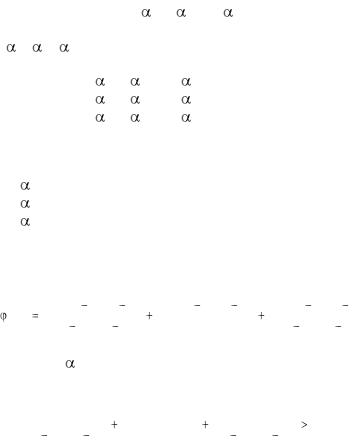
Таким образом, если известны значения функции f(x) в трех различных точках ak, xk, bk, равные соответственно f(ak), f(xk), f(bk), то функция f(x) может быть аппроксимирована квадратичной функцией

φ2(x) =		0 +	1·x1+	2·x2,	(2.2.1)
где 0, 1, 2 определяется из уравнений
0	+	1·ak +	2·ak2 = f(ak),
0	+	1·xk +	2·xk2	= f(xk),	(2.2.2)
0	+	1·bk +	2·bk2	= f(bk).

После преобразований уравнений (2.2.2) получаем

0 = [xkbk(bk-xk)f(ak) + bkak(ak-bk)f(xk) + akxk(xk-ak)f(bk)]/

1 = [(xk2-bk2)f(ak) + (bk2-ak2)f(xk) + (ak2-xk2)f(bk)]/ ,

(2.2.3)

2 = [(bk-xk)f(ak) + (ak-bk)f(xk) + (xk-ak)f(bk)]/

где = (ak-xk)(xk-bk)(bk-ak).

Интерполяционный многочлен

2 (x)

f (ak )(x

xk )(x

bk )

f (xk )(x

ak )(x

bk )

f (bk )(x

ak )(x

xk )

(2.2.4)

(ak

xk )(ak

bk )

(xk - ak )(xk - bk )

(bk ak )(bk

xk )

имеет минимум

bk]

только

x во внутренней точке интервала [ak,

тогда, когда

> 0, т. е. когда для совокупности “удачных точек”

выполняется неравенство

f (ak )

f (xk )

f (bk )

(2.2.5)

(ak

xk )(ak

bk )

(xk - ak )(xk - bk )

(bk

ak )(bk xk )

В этом случае из условия dφ2(x)/dx = 0 нетрудно получить,

что

[(xk 2 - bk 2 )f(ak )

(bk 2 - ak

2 )f(xk )

(ak

2 - xk 2 )f(bk )]

(2.2.6)

2[(xk - bk )f(ak ) (bk - ak )f(xk )

(ak - xk )f(bk )]

После проведения

испытаний

одним

из

рассмотренных в

предыдущем

параграфе

методов

точке

осуществляется

сокращение интервала неопределенности, содержащего точку минимума x*, и определяется новая совокупность “удачных точек”,

при этом возможны четыре случая:
~	~		*	находится в
1) если x	< xn и f( x ) < f(xn), точка минимума x			находится в
		~
интервале [ak, xk], и ak = ak, bk = xk, xk = x (рис. 2.2.1а);
~	~		*	находится в
2) если x	< xn и f( x ) ≥ f(xn), точка минимума x			находится в
	~	~
интервале [ x , bk], и ak =		x , bk = bk, xk = xk (рис. 2.2.1б);
~	~		*	находится в
3) если x	> xk и f( x ) < f(xn), точка минимума x			находится в
		~
интервале [xk, bk], и ak = xk, xk = x ,bk = bk (рис. 2.2.1в);
~	~		*	находится в
4) если x	> xk и f( x ) ≥ f(xk), точка минимума x			находится в
	~	~
интервале [ak , x ], и ak = ak, xk = xk, bk = x (рис. 2.2.1г);
f		f

0	ak x	xk bk	x	0 ak x xk bk	x
	~			~
	а)			б)
f				f

0 ak	xk	x	bk	x 0 ak	xk	x	x
		~				~
	в)				г)

Рисунок 2.2.1. Определение новой совокупности “удачных точек”

будет определить

Следует отметить, что, если точность ε задана слишком

малой, то ak, xk, bk и соответствующие им значения f(ak), f(xk), f(bk)

будут очень близки друг к другу, величину x

практически невозможно.

2.2.3. Кубическая интерполяция

Для четырех точек испытаний (m = 4) поиск минимума унимодальной функции f(x) можно вести с помощью метода кубической интерполяции (м. Давидона), который отличается от метода квадратичной интерполяции тем, что в нем в качестве интерполирующего полинома φn(x) используется кубическая парабола

φ3(x) = 0 + 1·x + 2·x2 + 3·x3,

(2.2.7)

что обеспечивает большую точность вычислений.

Функция (2.2.7) имеет один максимум и один минимум, если выполняется неравенство

22 ≥ 3 1 3.

В этом случае точка минимума ~ полинома φ (x) определяется по x 3

формуле

~	+ (bk	a k )	~	,
x = a k

где

~ = 1, если

Значение получаем из следующей формулы:

2		4	2	12
2	2	4	2	12	1	2
1,2 =							.
1,2 =		6	3				.
		6	3

Далее, аналогично методу квадратичной интерполяции, процедура поиска минимума унимодальной функции f(x) связана с

<<< < Предыдущая 1 23 / 163 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20223.17 Mб17Учебное пособие 1961.pdf
#
30.04.20223.21 Mб4Учебное пособие 1962.pdf
#
30.04.20223.22 Mб3Учебное пособие 1963.pdf
#
30.04.20223.23 Mб7Учебное пособие 1964.pdf
#
30.04.20223.23 Mб7Учебное пособие 1965.pdf
#
30.04.20223.23 Mб8Учебное пособие 1966.pdf
#
30.04.20223.23 Mб6Учебное пособие 1967.pdf
#
30.04.20223.25 Mб3Учебное пособие 1968.pdf
#
30.04.20223.26 Mб4Учебное пособие 1969.pdf
#
30.04.2022324.21 Кб2Учебное пособие 197.pdf
#
30.04.20223.31 Mб6Учебное пособие 1970.pdf