
Учебное пособие 1848
.pdf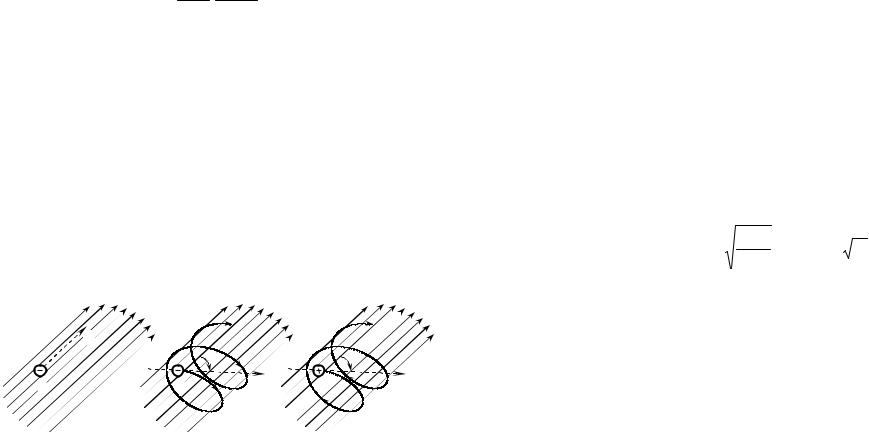
плазмы. Электроны и ионы, векторrскорости v |
которых ори- |
||
ентирован к силовым линиям поля H0 |
под углом ϕ, отличным |
||
от нуля, испытывают действие силы Лоренца |
|
||
r |
r |
] |
(3.36) |
Fл =q µ0 [ v |
H0 |
||
и начинают двигаться по круговой цилиндрической спирали, "навитой" вокруг линий магнитного поля под тем же углом и имеющей радиус
Rн = mqv0 µ0 vH0 sinϕ
(q, m − заряд и масса частицы; v0 − скорость света; v=|v|). На-
правление "навивки" спиральной траектории (левой или правой) зависит от знака электрическогозарядачастицы(рис.3.8).
Таким образом, постоянное магнитное поле, наводя определенный порядок в движении заряженных частиц плазмы, создает асимметрию пространственного распределения их скоростей. Теперь уже электромагнитные волны в разных направ-
лениях (например, вдоль или поперек H0 ) распространяются
по-разному. Плазма становится анизотропной. В уравнениях Максвелла это новое свойство намагниченной плазмы отражается введением тензора относительной диэлектрической проницаемости:
H0 H0 H0
v
|
|
ϕ |
|
ϕ |
q |
q |
v |
q |
v |
|
|
Рис. 3.8 98
|
εt |
|
|
|
ε |
−i ε |
0 |
|
|
|
|
|
|
|||
|
= |
i ε |
ε |
0 |
|
|
, |
|
|
(3.37) |
||||||
|
|
|
|
|
|
0 |
0 ε33 |
|
|
|
|
|||||
|
|
|
|
|
|
ωпл2 |
ω+i ϑ |
|
|
|||||||
ε=1− |
|
|
|
|
|
|
|
|
ω |
|
, |
(3.38) |
||||
|
(ω+i ϑ)2 −ωц2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
ω2 |
|
ω |
|
|
|
||||
ε |
|
= |
|
|
пл |
|
|
|
|
ц |
, |
|
(3.39) |
|||
(ω+i |
ϑ)2 −ω2 |
|
ω |
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
ц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|
ε33 =1− |
пл |
|
|
|
. |
|
|
(3.40) |
||||||
|
|
ω (ω+i ϑ) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В (3.38)-(3.40) введены обозначения: |
|
ωц − частота вращения |
||||||||||||||
заряженной частицы вокруг силовых линий H0 при движении
по спиральной траектории (называется также циклотронной частотой), вычисляется по формуле (3.14); ϑ− частота упругих соударений в плазме электронов и нейтральных частиц (атомов и молекул), она определяет потери энергии электромагнитной волны, идущей на разогрев плазмы; ωпл − круговая
частота так называемых электронных плазменных колебаний:
ω = |
n |
e2 |
≈1.8π 10 |
4 |
n |
(3.41) |
e |
m |
|
||||
пл |
ε0 |
|
|
e |
|
|
|
|
|
|
|
( ne , 1/см3 − концентрация электронов), которые возникают са-
мопроизвольно в результате случайного пространственного разделения в плазме электронов и ионов и появления в связи с этим электростатических сил взаимного притягивания, приводящих электроны в колебательное движение (ленгмюровские колебания); ω − круговаячастотаэлектромагнитнойволны, распространение которой нас интересует.
Анализ формул (3.37)-(3.40) дает возможность выявить важные особенности взаимодействия электромагнитных волн с
99
намагниченной плазмой. Полное совпадение вида тензоров ε (3.37) и µt (3.15) позволяет, не выполняя подробного исследо-
вания, сделать вывод о том, что в намагниченной плазме мы встретимся с теми же эффектами, с которыми познакомились в разделе 3.3: эффектом Фарадея и явлением двойного лучепреломления. Разница будет лишь в том, что, если в намагниченном ферримагнетике влияние анизотропии среды сказывалось на поведении магнитной составляющей распространяющейся волны, то в анизотропной плазме это влияние отразится на электрической составляющей. При отсутствии потерь ( ϑ=0 , такая плазма называется бесстолкновительной) компоненты тензора диэлектрической проницаемости ε и ε бесконечно возрастают, когда ω= ωц. Это свидетельствует о развитии в плазме резонансного процесса. В намагниченном ферримагне-
тике в подобной ситуации (см. (3.16)) возрастает амплитуда r
прецессии магнитных моментов m атомов вокруг поля H0 :
наступает ферромагнитный резонанс. В намагниченной плазме резонансным образом увеличивается радиус спиральной траектории движения заряженных частиц (циклотронный резонанс). В плазме легко достигаетсяt также ситуация, когда диагональные компоненты тензора ε (3.38), (3.40) принимают нулевое значение. Это явление известно как плазменный резонанс, суть которого заключается в раскачке электромагнитной волной ленгмюровских колебаний в плазме. В диапазоне частот, где ω< ωпл, диэлектрическая проницаемость плазмы становится отрицательной: волны в такой среде распространяться не могут (явление отсечки). Компоненты тензора ε, а следовательно, и связанные с ними показатель преломления плазмы, фазовая скорость волны зависят от ее частоты. Поэтому в плазме наблюдается заметная дисперсия волн.
Перечисленные явления не исчерпывают всех особенностей плазмы, однако и они уже свидетельствуют о большом разнообразии эффектов, сопровождающих процесс взаимодействия электромагнитных волн с этой средой.
100
Рассмотрим подробнее распространение электромагнитных волн в намагниченной плазме. Пусть постоянное во вре-
мени однородное магнитное поле H0 , ориентированное под
углом Θ к оси Оz, пронизывает пространство, заполненное бесстолкновительной плазмой (учет потерь серьезно загромоздил бы математические выкладки, лишив их наглядности; влияние же потерь в среде на распространение волн рассмотрено в разделе3.2). Если плоская электромагнитная волна бежит в подобных условиях вдоль оси Оz, то, как показывает подробный анализ уравнений Максвелла, показатель преломления плазмы описывается выражением
n2 |
=1− |
|
|
|
|
ω2 |
|
|
|
, (3.42) |
|
|
|
|
|
|
пл |
|
|
|
|||
пл |
|
ω2 |
ω2 |
|
|
|
ω2 |
ω2 |
|
|
2 |
|
|
|
|
|
|||||||
|
ω2 − |
ц |
|
|
± |
|
ц |
|
|
|
+ ω2 ωц2|| |
|
2 (ω2 −ω2 |
) |
2 (ω2 −ω2 |
) |
|||||||
|
|
|
|
|
|
||||||
|
|
|
пл |
|
|
|
пл |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
где ωц =ωц sinΘ, ωц|| =ωц cosΘ − соответственно"поперечная"
и "продольная" циклотронные частоты. Амплитуды поперечных составляющих электрической компоненты волны определяются соотношением
E&m y = |
|
|
ωц2 |
ω |
|
|
ωц2 |
ω |
|
2 |
|
|
|
|
m |
|
+ |
|
(3.43) |
||||||||
E&m x |
i |
|
2 (ω2 −ωпл2 )ωц|| |
|
|
|
|
|
|
|
1 . |
|
|
|
|
|
|
2 (ω2 −ωпл2 )ωц|| |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Связь продольной составляющей электрической компоненты с поперечными имеет вид
|
|
|
|
ω ω |
ц |
ω2 |
|
|
|
ω |
|
|
|
|
||
E& |
|
= |
|
|
|
пл |
|
|
|
ц|| |
E& |
|
−i E& |
. |
(3.44) |
|
|
ω2 ω2 |
−(ω2 −ω2 |
) (ω2 |
−ω2 |
|
|
|
|||||||||
|
z |
|
) |
ω |
x |
|
y |
|
||||||||
|
|
|
ц |
|
|
пл |
|
ц|| |
|
|
|
|
|
|
|
|
Проанализируем частные случаи.
101

Распространение плоской волны в плазме вдоль поля намагничивания
При продольном распространении (Θ= 0°) векторы H0 и
Пr бегущей волны ориентированы параллельно оси Оz. Поэтому ωц =0, ωц|| =ωц и из формулы (3.42) следует, что
2 |
ωпл2 |
|
|
|
nпл = 1− |
|
. |
(3.45) |
|
ω (ω±ωц) |
||||
|
|
|
Знаки "±" в (3.45) свидетельствуют о том, что уравнения Максвелла для сформулированной задачи имеют два решения, т.е. первоначальная плоская линейно-поляризованная волна "распадается" на две волны, бегущие в общем Оz-направлении с постоянными распространения
k(+) =ω ε |
|
µ |
|
n(+) =ω |
ε |
|
µ |
|
|
1 − |
ω2 |
, |
(3.46,a) |
0 |
0 |
0 |
0 |
пл |
|||||||||
|
|
|
|
|
|
|
ω(ω+ωц) |
|
|
||||
k(−) =ω ε |
|
µ |
|
n(−) =ω |
ε |
|
µ |
|
|
1 − |
ω2 |
. |
(3.46,б) |
0 |
0 |
0 |
0 |
пл |
|||||||||
|
|
|
|
|
|
|
ω(ω−ωц) |
|
|
Как видно, "−"- волна бежит быстрее "+"- волны:
v(+) = |
ω |
<v(−) = |
ω |
. |
(3.47) |
|
|
||||
ф |
k(+) |
ф |
k(−) |
|
|
|
|
|
|||
Определим поляризацию электрической компоненты каждой волны. Из (3.44) с учетом ωц =0 следует, что E&z(+),(−) =0 , т.е.
обе волны являются чисто поперечными. Составляющие E&x и E&y , как показывает (3.43), равны по модулю и сдвинуты по фазе на 90°:
E& |
=±i E& |
. |
(3.48) |
m y |
m x |
|
|
Следовательно, Е- компоненты двух электромагнитных волн, возникающих при продольном распространении плоской вол-
102
ны в намагниченной плазме, поляризованы по кругу в противоположных направлениях. Условия (3.48) и (3.47) приводят к выводу о наличии эффекта Фарадея при рассматриваемых условиях взаимодействия плоской волны с плазмой (сравнить с выводами, вытекающими из формул (3.23), (3.25), (3.27)).
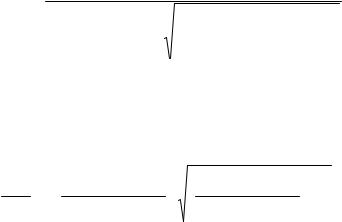
Рассмотрим задачу, иллюстрирующую необходимость учета эффекта Фарадея на практике. Предположим, что два космических аппарата, вращающихся вокруг Земли на высоте 300 км, снабжены антеннами в виде симметричных вибраторов. Пусть антенны параллельны друг другу. Между аппаратами ведется обмен информацией на частоте 30 МГц, причем радиоволны распространяются в направлении, параллельном силовым линиям магнитного поля Земли. При каком взаимном удалении аппаратов в результате действия эффекта Фарадея связь между ними прервётся?
Решение. Указанное событие произойдет в том случае, если на трассе, разделяющей космические аппараты, плоскость
поляризации вектора |
E& |
радиоволны |
повернется |
на 90° |
|||||
(рис. 3.9). Это будет иметь место при условии (3.28) |
|
||||||||
|
|
|
1 |
(k(+) − k(−) ) l=π/2. |
|
|
|||
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||
Примем |
ω = 2,8·π·106 |
с−1, |
ne = 106 1/см3 |
(рис. 3.12), |
следова- |
||||
|
ц |
ω = 1,8·π·107 с−1 (3.41). Тогда, пользуясь |
|||||||
тельно, |
частота |
||||||||
|
|
пл |
|
|
|
|
|
|
|
(3.46,а,б), легко вычислить: ℓ= π/(k(+) − k(−) ) ≈1133 м. |
|
||||||||
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
E |
|
ℓ |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
Рис. 3.9 |
|
|
||
|
|
|
|
|
103 |
|
|
|
|
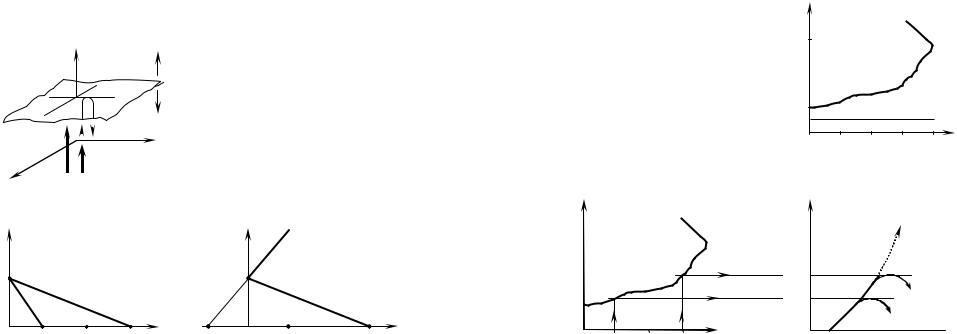
Исследуем теперь явление отсечки. Как уже отмечалось, волны теряют способность распространяться в среде с ε< 0 (n − мнимая величина) и отражаются от границы, где εпл и nпл равны нулю (рис. 3.10). Тогда условие отсечки
ε =n2 |
=1− |
ωпл2 |
=0 |
(3.49) |
||||||
ω (ω±ωц) |
||||||||||
|
пл |
|
пл |
|
|
|
||||
|
|
|
|
|
|
|
|
|||
выполняется при |
|
|
ω |
2 |
|
ω |
|
|
||
|
|
|
|
|
|
|||||
|
|
|
пл |
=1± |
ц |
. |
|
(3.50) |
||
|
|
|
|
|||||||
|
|
|
ω |
|
ω |
|
|
|||
На рис. 3.11 показано изменение относительной диэлектрической проницаемости плазмы (или, что то же самое, nпл2 ) в за-
висимости от квадрата соотношения частот волны и плазменных колебаний. Рис. 3.11,а справедлив для волн с частотами,
|
|
|
|
|
|
|
превышающими |
циклотрон- |
||||
|
|
z |
|
2 |
|
ную ωц ; рис. 3.11,б − для си- |
||||||
|
|
|
|
|
nпл |
<0 |
туации ω< ω . |
|
|
|
||
|
|
|
|
|
nпл2 |
=0 |
|
|
ц |
|
|
|
|
|
|
|
|
nпл2 |
>0 |
|
Воспользуемся получен- |
||||
r |
|
|
|
|
ными выводами для качест- |
|||||||
|
|
|
|
|
|
венного анализа отсечки элек- |
||||||
|
|
|
|
|
|
|||||||
H0 |
|
|
|
|
y |
|
тромагнитных волн в ионо- |
|||||
|
|
|
|
|
||||||||
|
волна |
|
||||||||||
x |
|
|
|
сфере Земли, когда распро- |
||||||||
Рис. 3.10 |
|
|
|
странение можно назвать про- |
||||||||
|
|
|
|
|
|
|
|
|
||||
εпл |
|
|
|
|
|
|
|
εпл |
εпл(−) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
ε(−) |
|
|
|
εпл(+) |
ω |
2 |
|
|
|
εпл(+) |
ω |
2 |
пл |
|
|
|
|
пл |
) 1−ωωц 0 |
|
|
|
|
пл |
|
0 1−ωωц |
1 |
|
1+ωωц |
( ω |
|
1 |
1+ωωц ( ω ) |
|||||
|
|
а |
|
|
Рис. 3.11 |
|
б |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
104 |
|
|
|
|
|
дольным (волна должна бежать вдоль силовых линий магнитного поля Земли). На рис. 3.12 приведен качественный характер изменения концентрации свободных электронов в ионосфере по мере подъема над поверхностью Земли (точный профиль ионосферы измеряется экспериментально). Поскольку
(см. (3.41)) ne ~ ωпл2 , при фиксированной частоте волны ось абсцисс на рис. 3.12 можно разметить в единицах параметра ωпл2 /ω2 (рис. 3.13,а). Если принять, что напряженность посто-
янного магнитного поля Земли составляет H0 = 40 A/м, то циклотронная частота (3.14) будет равняться ωц = 2,8·π·106 с−1
(fц= 1,4 МГц). Пусть частота плоской линейно-поляризованной |
||||||||||
волны |
больше |
циклотронной |
частоты (ω> ωц= 2,8·π·106 с−1, |
|||||||
f > fц= 1,4 МГц). |
Тогда |
траек- |
|
h, км |
|
|
|
|
||
тории движения в ионосфере |
|
|
|
|
|
|||||
"+" и "−"- волн будут иметь |
300 |
|
ионосфера |
|
|
|
|
|||
вид, |
показанный |
на |
|
|
|
|
|
|||
рис. 3.13,б (сплошные кри- |
|
|
|
|
|
|
|
|||
вые). Отсечка (поворот к Зем- |
|
|
|
|
|
|
|
|||
ле) "+" и"−"- волнпроисходит |
60 |
|
стратосфера |
|
n , |
эл.3 |
||||
соответственно на разных вы- |
|
|
тропосфера |
|
||||||
сотах h(+) и h(−). Если частота |
102 |
103 104 105 |
106 |
e |
см |
|
||||
|
|
|
||||||||
волны меньше циклотронной |
|
|
Рис. 3.12 |
|
|
|
|
|||
h |
|
|
|
|
h |
|
|
|
|
|
ионосфера |
|
|
|
|
"−"- волна |
|
|
|
|
|
|
|
|
|
(f < fц ) |
|
|
|
|
||
|
|
|
|
h(+) |
|
"+"- волна |
|
|
||
|
|
|
|
h(−) |
|
|
|
|||
1−ωωц 1 |
1+ωωц |
(ωωпл)2 |
|
|
"−"- волна |
|
|
|
||
|
|
земля |
|
|
|
|
||||
|
а |
|
Рис. 3.13 |
б |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
105 |
|
|
|
|
|
|
|

(f < fц), "+"- волна по-прежнему испытывает отсечку на высоте h(+) , a "−"- волна уходит вглубь ионосферы, не возвращаясь к Земле (рис. 3.13,б, штриховая кривая).
Распространение плоской волны в плазме поперек поля намагничивания
При поперечном распространении (волна по-прежнему бежит вдоль оси Оz, вектор напряженности поля H0 лежит в
плоскости хОу, например, вдоль оси Оx) угол Θ составляет 90°, поэтому ωц =ωц, ωц|| =0 . Уравнения Максвелла вновь приво-
дят к двойному решению (см. (3.42)), т.е. распространяющаяся волна разбивается на две волны. Для первой из них (она называется обыкновенной)
n(об)2 |
=1−ωпл2 . |
(3.51) |
пл |
ω2 |
|
|
|
Видно, что nпл(об) совпадает со значением nпл для ненамагниченной (изотропной) плазмы (см. (3.42) при ωц =ωц|| =0 ). В обыкновенной волне, если обратиться к (3.43), (3.44),
&(об) |
|
|
|
|
|
|
|
|
E |
|
&(об) |
|
& |
(об) |
|
|
|
m y |
|
|
|
|
||||
|
=0, |
E |
|
≠0, |
E |
m y |
=0, |
(3.52) |
&(об) |
|
|||||||
|
m x |
|
|
|
|
|||
E |
|
|
|
|
|
|
|
|
m x |
|
|
|
|
|
|
|
|
|
|
& |
(об) |
=0. |
|
|
|
(3.53) |
|
|
E |
m z |
|
|
|
||
|
|
|
|
|
|
|
|
|
Таким образом, обыкновенная волна распространяется вдоль оси Оz и имеет только однуrэлектрическую составляющую
E&m(обx ) , параллельную вектору H0 . Волна эта ведет себя в плаз-
ме так, будто поле Н0 отсутствует. Поэтому свойства ее не отличаются от свойств плоской линейно-поляризованной волны, бегущей в любом направлении в изотропной плазме. Постоянная распространения и фазовая скорость обыкновенной волны равны соответственно
106
k(об) =ω  ε0 µ0 nпл(об) =ω
ε0 µ0 nпл(об) =ω  ε0 µ0
ε0 µ0  1−(ωпл /ω)2 ,
1−(ωпл /ω)2 ,
v(об) = ω |
= |
1 |
. |
|
ф |
k(об) |
|
ε0 µ0 1−(ωпл /ω)2 |
|
|
|
|
||
Обыкновенная волна испытывает отсечку ( nпл(об) =0 ) при
|
ω |
2 |
(3.54) |
|
|
пл |
= 1. |
||
|
ω |
|
|
|
Второе решение уравнений Максвелла для задачи о поперечном распространении волн в намагниченной плазме соответствует волне, которую называют необыкновенной:
(н)2 |
|
ωпл2 |
|
|||
nпл |
=1− |
|
|
. |
(3.55) |
|
2 |
ω2 ωц2 |
|||||
|
|
ω − |
|
|
|
|
|
|
ω2 −ω2 |
|
|||
|
|
|
пл |
|
||
У этой волны (см. (3.43), (3.44))
|
|
&(н) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
E |
|
&(н) |
|
|
& |
(н) |
|
|
|
|
|||
|
|
|
m y |
|
|
|
|
|
|
|
|||||
|
|
|
|
=∞, |
E |
|
≠0, |
E |
m x |
=0, |
|
|
(3.56) |
||
|
|
&(н) |
|
|
|
||||||||||
|
|
|
m y |
|
|
|
|
|
|
||||||
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
m x |
|
|
|
|
|
|
|
|
|
|
|
|
&(н) |
|
|
ω ω ω2 |
|
|
|
& |
(н) |
|
|
|||||
|
|
|
ц |
|
пл |
|
|
|
|
|
|||||
E |
m z |
= |
|
|
|
|
|
|
|
(i E |
m y |
). |
(3.57) |
||
ω2 (ω2 −ω2 |
)−ω2 |
ω2 |
|||||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
пл |
|
|
|
ц |
|
|
|
|
|
|
Следовательно, необыкновенная волна, распространяясь, как и обыкновенная, вдоль оси Оz, имеет две составляющие элек-
трической компоненты (E&m(нz) , E&m(нy) ) , которые не равны по моду-
лю и сдвинуты по фазе на 90°. Поэтому вектор E&(н) необыкновенной волны поляризован по эллипсу, плоскость которого
перпендикулярна H0 . Необыкновенная волна характеризуется постоянной распространения
k(н) = ω ε |
0 |
µ |
0 |
n(н) |
(3.58) |
|
|
пл |
|
||
107 |
|
|
|
|
|
и перемещается с фазовой скоростью |
|
||
v(н) = |
ω |
, |
(3.59) |
|
|||
ф |
k(н) |
|
|
|
|
|
|
отличной от скорости движения обыкновенной волны. Проанализируем отсечку необыкновенной волны. При-
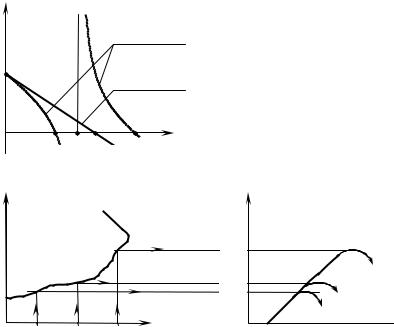
равнивая показатель преломления nпл(н) , определяемый формулой (3.55), к нулю, легко найти, что это требование выполняется при (ωпл /ω)2 =1± ωц /ω. Зависимость от квадрата параметра ωпл /ω относительной диэлектрической проницаемости плаз-
мы (или n(н) 2 ) дляобыкновенной и необыкновенной волн при- |
|||||||||
|
|
пл |
|
|
|
|
|
|
|
ведена на рис. 3.14 (рассмотрен случай ω>ωц ). |
|
|
|||||||
|
|
|
|
Направляя с поверхности Зем- |
|||||
|
εпл |
|
|
ли |
радиолуч так, |
чтобы он |
|||
|
|
|
был |
перпендикулярен |
сило- |
||||
|
|
необыкновенная |
|||||||
|
|
вым линиям магнитного поля |
|||||||
|
ω>ωц |
волна |
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
обыкновенная |
Земли, можно по аналогии с |
|||||
|
|
рис. 3.13 |
графически опреде- |
||||||
|
|
|
волна |
лить высоты, на которых про- |
|||||
|
|
|
(ωωпл)2 |
||||||
0 |
|
1 |
изойдет |
отсечка |
обыкновен- |
||||
1−ωц |
1−ωц2 |
1+ωц |
ной |
и необыкновенной |
волн |
||||
|
ω |
ω2 |
ω |
(рис. 3.15). |
|
|
|||
|
h |
Рис. 3.14 |
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ионосфера |
|
h(н)′′ |
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
h |
(об) |
необыкнов. |
|||
|
|
|
|
|
|
|
волна |
||
|
|
|
|
h(н)′ |
обыкнов. волна |
||||
|
|
|
1+ωωц (ωωпл)2 |
|
|
|
необыкнов. волна |
|
|
|
1−ωωц |
1 |
|
|
|
земля |
|
|
|
|
|
а |
Рис. 3.15 |
|
б |
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
108 |
|
|
|
|
|
3.5. Волны в анизотропных кристаллах
Стремительное развитие лазерной техники потребовало разработки устройств для модуляции и управления параметрами когерентного излучения лазеров. Наиболее перспективными и нашедшими широкое применение в практике оказались устройства, использующие электрооптические и магнитооптические эффекты.
К электро- и магнитооптическим относят явления взаимодействия электромагнитных волн оптического диапазона со средами, показатель преломления которых изменяется под влиянием специально приложенного электрического или магнитного поля.
Среди электрооптических в технике чаще других используются эффекты Керра и Поккельса, среди магнитооптических − эффекты Фарадея и Коттона-Мутона. Все перечисленные явления являются следствием анизотропных свойств кристаллов.
Остановимся кратко на основных вопросах кристаллооптики. Начнем со следующего мысленного эксперимента. Предположим, что внутри прозрачной кристаллической среды включен источник электромагнитного (видимого) излучения, обладающий сферической формой собственной диаграммы направленности. Проследим за процессом распространения в толще кристалла фронта оптической волны. Если через некоторое время после включения источника сфотографировать извне прозрачный образец и ту область пространства ("оптическое тело"), которая к моменту фотосъемки будет заполнена излучаемым светом, то выяснится, что для различных сред результаты эксперимента окажутся разными: в одних средах "оптическое тело" будет окружено сферической поверхностью, представляя собой световой шар, в других – иметь вид эллипсоида вращения (двухосный эллипсоид), в третьих – трехосного эллипсоида. Первый результат относится к изотропной сре-
109
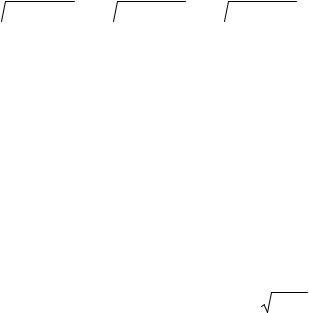
де, в которой скорость распространения фронта оптического излучения одинакова во всех направлениях. Изотропными оказываются симметричные кристаллы с кубической решеткой. Второй и третий результаты наблюдаются в анизотропных средах (это кристаллы с любой другой структурой решетки кроме кубической). Указанные поверхности, в каждой точке которых волновой вектор волны, распространяющейся в среде, принимает постоянное значение, называют оптической индикатрисой кристалла.
Уравнение, описывающее поверхность индикатрисы, не-
трудно вывести, исходя из материального |
уравнения (1.23) |
||||
r |
t r |
и соотношения (1.41) для плотности электрической |
|||
D =ε0 |
ε Е |
||||
энергии поля w = |
1 |
E D . Так как |
|
||
2 |
|
||||
|
|
Э |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
Di =∑ε0 εik Ek |
(3.60) |
k=1
( εik − компонента тензора εt; i, k – индексы, принимающие значения 1,2,3), то
|
|
|
3 |
|
|
ε0 |
|
3 |
3 |
|
|
|
|
||
wЭ = |
1 |
∑Ei Di = |
∑∑Ei εik Ek = |
|
|||||||||||
2 |
2 |
|
|||||||||||||
|
ε0 |
|
i=1 |
|
|
|
|
|
i=1k=1 |
|
|
|
|
||
= |
|
(ε |
E2 |
+ε |
22 |
E2 |
+ε |
33 |
E2 |
+ |
(3.61) |
||||
|
|
||||||||||||||
2 |
11 |
x |
|
|
y |
|
z |
|
|
||||||
+2 ε12 Ex Ey +2 ε13 Ex Ez +2 ε23 Ey Ez ).
Как видно, (3.61) по форме записи совпадает с уравнением поверхности 2-го порядка. Громоздкость выражения (3.61) объясняется тем, что оно записано для системы координат xyz, оси которой совершенно произвольно ориентированы относительно ребер атомной решетки кристалла. Поворачивая Оx, Оy, Оz, можно совместить их с так называемыми главными диэлектрическими осями кристалла ОX, ОY, ОZ. В новых координатах X, Y, Z тензор ε принимает диагональный характер ( εik =0
при i ≠k), и поэтому выражение (3.61) упрощается: 110
|
|
w = |
1 |
ε |
0 |
(ε |
X |
E2 |
+ε |
Y |
E2 |
+ε |
Z |
E2 ) |
(3.62) |
|||||||||
|
|
|
||||||||||||||||||||||
|
|
|
Э |
2 |
|
|
|
|
X |
|
|
Y |
|
|
Z |
|
||||||||
или |
|
D2 |
|
|
|
|
|
|
|
|
|
D2 |
|
|
|
|
|
|
D2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
X |
|
+ |
|
|
|
Y |
|
|
+ |
|
|
Z |
|
=1. |
(3.63) |
||||||
|
2ε |
0 |
ε |
w |
2ε |
0 |
ε |
w |
|
2ε |
0 |
ε |
w |
|||||||||||
|
|
X |
|
|
Э |
|
|
|
|
Y |
Э |
|
|
|
Z |
Э |
|
|||||||
Мы получили каноническое уравнение поверхности 2-го порядка с центром симметрии. Оси ОX, ОY, ОZ являются осями симметрии поверхности, представляющей собой трехосный эллипсоид, полуоси которого равны
a= 2ε0 εX wЭ , b=
2ε0 εX wЭ , b= 2ε0 εY wЭ , c=
2ε0 εY wЭ , c= 2ε0 εZ wЭ. (3.64)
2ε0 εZ wЭ. (3.64)
Помимо формы оптической индикатрисы для выяснения особенностей распространения волн в анизотропных кристаллах большое значение имеет уравнение Френеля для волновых векторов. Для плоской волны, распространяющейся в объеме кристалла,
& & |
|
|
|
r r |
|
|
& |
& |
|
|
|
|
r r |
|
|
|
|
e |
i (ωt−k r ) |
, |
|
|
|
e |
i (ωt−k r ) |
. |
(3.65) |
||||
E =E |
|
|
|
H =H |
m |
|
|||||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнения Максвелла |
|
|
|
|
|
|
|
|
|
|
|
|
|||
& |
|
|
& |
|
& |
|
& |
|
|
& |
|
|
|||
rotE |
=−i ω µa |
H , |
rotH =i ω D |
|
|
||||||||||
можно записать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|||
[kr E& |
|
]=ω µ H& |
m |
, |
[kr H& |
m |
]=−ω D&. |
(3.66) |
|||||||
m |
|
|
a |
|
|
|
|
|
|
|
|
||||
Учитывая (3.60), а также вводя вектор K =k /(ω ε0 µ0 ) , пару уравнений (3.66) можно заменить одним уравнением
r r |
& |
|
t |
& |
|
(3.67) |
[K [K E |
]]=−ε E . |
|||||
|
|
m |
|
|
m |
|
Раскрывая двойное векторное произведение и переходя к проекциям на главные оси кристалла, (3.67) можно заменить тремя скалярными уравнениями вида
111
3 |
|
∑E&k (εik +Ki Kk −K 2 δik )=0, |
(3.68) |
k=1
где символ Кронекера
δ = 1, i =k,
ik 0, i ≠k (i, k =1,2,3).
Нетривиальное решение системы однородных линейных уравнений (3.68) находится приравниванием к нулю её определителя:
εX −K 2 +KX2 |
KY KX |
KZ KX |
|
KX KY |
εY −K 2 +KY2 |
KZ KY |
= 0. (3.69) |
KX KZ |
KY KZ |
εZ −K 2 +KZ2 |
|
Записанное в развернутом виде уравнение (3.69) известно как уравнение Френеля:
K 2 (εX KX2 +εY KY2 +εZ KZ2 )−[εX (εY +εZ ) KX2 + (3.70)
+εY (εZ +εX ) KY2 +εZ (εX +εY ) KZ2 ]+εX εY εZ = 0.
Квадратичность (3.70) относительно K2 (или k2) следует понимать как свидетельство того, что в анизотропной кристаллической среде плоская монохроматическая волна (3.65) при распространении в произвольном направлении разбивается на две волны. Подробный анализ показывает, что обе волны всегда поляризованы линейно в перпендикулярных друг другу плоскостях. Таким образом, в отличие от изотропных сред, где одинаковое право на существование имеют линейно-, кругло- и эллиптически-поляризованные волны, в анизотропной кристаллической среде волны с двумя последними видами поляризации распространяться не могут (исключение составляет частый случай, когда исходная плоская волна (3.65) бежит точно вдоль главной оси). Отмеченные волны движутся в кри-
112
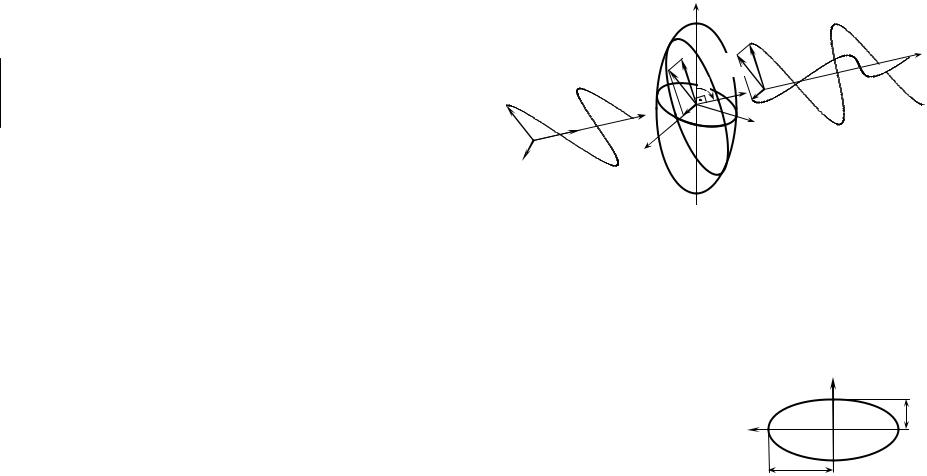
сталле в одном направлении с разными скоростями, а следовательно, имеют разную длину. Направление поляризации волн и показатели преломления среды для каждой волны определяются с помощью оптической индикатрисы. С этой целью строится сечение индикатрисы плоскостью перпендикулярной к
волновому вектору K падающей волны (рис. 3.16).
Z
D1 |
K |
|
r |
|
|
Dпад |
|
Dпад |
Ψ |
|
D2 |
||
K |
||
Y |
||
Hпад |
X |
|
|
Рис. 3.16
Главные оси эллипса сечения, изображенного на рис. 3.17, задают направления поляризации двух волн, возбуждаемых в
кристалле ( D1 и D2 ), а длина каждой главной полуоси − величину показателя преломления среды для соответствующей
волны. |
Существуют |
два |
таких |
направления вектора |
K |
||||
( Θ1 =−Θ2 =Θ), для которых се- |
|
|
r |
|
|||||
чение |
трехосного |
эллипсоида |
|
|
|
||||
имеет |
форму круга. |
Очевидно, |
|
|
D2 |
|
|||
r |
n2 |
||||||||
что в данных случаях волна, бе- |
|||||||||
D1 |
|||||||||
гущая в указанных направлени- |
|
|
|
|
|||||
ях, которые называют направле- |
|
|
|
|
|||||
ниями оптической оси кристал- |
|
n1 |
|
|
|||||
ла, по-прежнему |
может |
быть |
|
Рис. 3.17 |
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
113 |
|
|
|
|
|
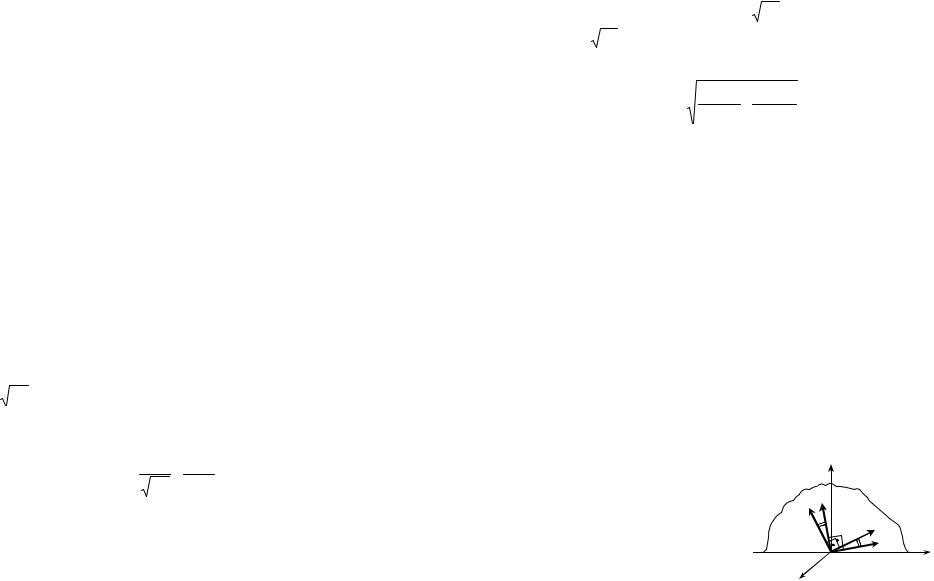
представлена комбинацией двух линейно-поляризованных волн. Однако скорости (и длины) этих волн одинаковы, а направления поляризации, оставаясь ортогональными, точно не определены. Кристаллы с оптической индикатрисой в виде трехосного эллипсоида ( a ≠b≠c , (3.64)), имеющие две оптические оси, называют двухосными. Очевидно, что если a =b≠c (3.64) и индикатриса описывается эллипсоидом вращения, то оптическая ось единственная и совпадает с кристаллографической осью. Такой кристалл называют одноосным.
Уравнение Френеля (3.70) для одноосного кристалла несколько упрощается:
(K 2 −εY ) [(KX2 +KY2 ) εY +KZ2 εZ −εY εZ ]=0. |
(3.71) |
Два решения, соответствующие уравнениям, вытекающим из
(3.71),
K 2 −εY =0, |
(3.72,а) |
(KX2 +KY2 ) εY +KZ2 εZ −εY εZ =0, |
(3.72,б) |
относятся к двум волнам, на которые в одноосном кристалле также разбивается падающая плоская волна при произвольном направлении распространения. Поверхность волновых векторов первой волны, как следует из (3.72,а), имеет вид сферы ра-
диусом εY =nY =n(об) . Следовательно, первая из двух волн
воспринимает кристалл как изотропную среду, имеет сферический фронт, распространяется со скоростью
v(об) = |
v0 |
= |
v0 |
|
εY |
|
n(об) |
и поляризована линейно в направлении либо малой полуоси эллипса сечения индикатрисы (для положительного кристалла εX =εY >εZ ), либо большой полуоси (для отрицательного кри-
сталла εX =εY <εZ ). Эту волну называют обыкновенной.
114
Поверхность волновых векторов второй волны (см. формулу (3.72,б)) совпадает с поверхностью эллипсоида враще-
ния, у которого одна полуось равна εY =n(об) (вдоль оси ОZ), а две другие εZ =n(н) (вдоль осей ОX и ОY). Вторая волна называется необыкновенной. Она движется со скоростью
v(н) =v |
sin2 Ψ +cos2 Ψ |
|
0 |
εZ |
εY |
|
|
|
(здесь Ψ − угол между вектором k и оптической осью кристалла) и поляризована линейно по одной из полуосей эллипса сечения оптической индикатрисы (перпендикулярно к обыкновенной волне). Необыкновенная волна пропадает, когда волновой вектор падающей волны совпадает с оптической осью кристалла. Таким образом, при распространении плоской электромагнитной волны в анизотропном кристалле (как в одно-, так и в двухосном) всегда (кроме случая Ψ= 0°) имеет место эффект двойного лучепреломления.
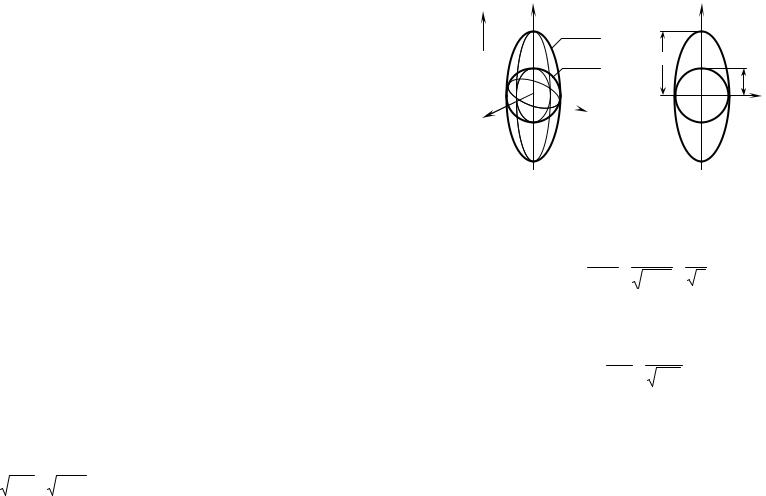
Дополнительные особенности волнового процесса, порождаемые анизотропией среды, вытекают из уравнений r(3.r66),r
Анализируя последние, легко установить, что векторы E,D,k , Пr всегда располагаются в одной плоскости, перпендикулярной вектору H , причем, если Ψ≠0 , векторы E и D непарал-
лельны и угол между ними равен углу между П и k . Следова- |
|||
тельно, в анизотропном кристал- |
|
|
|
ле фронт волны движется в на- |
|
z |
|
правлении, отличном от направ- |
|
|
|
|
D |
|
|
ления потока энергии, перено- |
E |
|
|
симой волной (рис. 3.18). |
П r |
|
|
В лазерной технике для |
|
y |
|
управления режимом излучения |
|
k |
|
x |
0 |
|
|
лазера хорошо зарекомендовали |
|
||
|
|
||
себя электрооптические модуля115
торы (затворы) на анизотропных кристаллах, в которых имеют место эффекты Керра и Поккельса.
Электрооптический эффект Керра
Эффект Керра (открыт шотландским физиком Дж. Керром в 1875 г.) наблюдается в кристаллах, решетка которых имеет центр симметрии (группа перовскитов ABO3, BaTiO3,
KTax Nb1−xO3 и др.), в жидких диэлектриках (нитробензол, се-
роуглерод, ацетон, этиловый спирт и др.) и в газах. Указанные вещества в обычном состоянии изотропны и характеризуются относительной диэлектрической проницаемостью ε. Однако во
внешнем однородном электрическом поле E&0 вследствие ори-
ентации вдоль него молекул, обладающих собственным дипольным моментом (ориентационный эффект), и индуцирования полем E0 дипольного момента в молекулах, которые не
имеют его в естественном состоянии (поляризационный эффект), эти вещества становятся анизотропными, переходя в класс одноосных кристаллов. При этом их оптическая индикатриса из сферы превращается в эллипсоид вращения (рис. 3.19,а), главная ось которого (оптическая ось кристалла)
ориентируется параллельно полю E&0 (рис. 3.19,б). Эффект Керра квадратичен:
ε(н) = ε(об) +K |
k |
E2 |
(3.73) |
|
0 |
|
( Kk =2π n(об) Bk − постоянная среды; Вk − постоянная Керра). Если теперь линейно-поляризованную волну пропустить сквозь указанную среду в направлении, перпендикулярном E&0
(скажем, вдоль оси ОY), она разобьется на обыкновенную и необыкновенную волны. Обыкновенная волна приобретет линейную поляризацию, параллельную оси ОX, и будет распро-
116
E0 |
Z |
|
Z |
E0 |
≠0 |
|
|
|
|
||
|
E0 = 0 |
n(н) |
|
|
|
Y |
n(об) |
X |
|
Y |
|
|
|
||
а |
Рис. 3.19 |
б |
|
|
|
||
страняться со скоростью |
|
|
|
v(об) = |
v0 |
= v0 |
= v0 . |
|
n(об) |
ε(об) |
ε |
Необыкновенная волна (также линейно-поляризованная, но вдоль оси ОZ) будет распространяться медленнее:
v(н) = |
v0 |
= v0 . |
|
n(н) |
ε(н) |
За счет различия скоростей v(об), v(н) обыкновенная и не-
обыкновенная оптические волны, пройдя в среде путь ℓ, приобретут фазовый сдвиг
|
1 |
|
1 |
2 |
|
|
∆Ф=ω l |
|
− |
|
|
≈2π Bk l E0 |
(3.74) |
|
|
|||||
v(н) |
|
v(об) |
|
|
||
(в (3.74) учтено, что Kk E02 <<ε(об) ), вследствие чего на выходе
из среды оптическая волна будет иметь эллиптическую поляризацию. При ∆Φ=π/ 2 и равенстве амплитуд обыкновенной и необыкновенной волн поляризация станет круговой.
117
