Дифференциальное исчисление функций, заданных аналитически (явно). Барсуков А. И., Ряжских В. И

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Воронежский государственный технический университет»

А. И. Барсуков, В. И. Ряжских, А. А. Седаев

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ, ЗАДАННЫХ АНАЛИТИЧЕСКИ (ЯВНО)

Учебное пособие

Воронеж 2018

§1. Задачи, приводящие к понятию производной функции в точке

Производная функции в точке является одним из важнейших понятий, связывающих математику с другими естественными науками. Именно она позволяет находить мгновенную скорость изменения переменной, определять участки ее возрастания и убывания, находить наибольшие и наименьшие значения, раскрывать неопределенности и легко решать другие практические задачи. Ниже обсуждаются две проблемы (одна – физическая, другая – геометрическая), которые демонстрируют естественность возникновения понятия производной.

Пример 1.1. (Задача о мгновенной скорости движения)

Пусть по числовой оси движется точка A, и пусть в каждый момент времени t известна величина S(t) отклонения точки A от точки отсчета O, взятая со знаком плюс, если A находится на положительной полуоси, и со знаком минус в противном случае. Например, если S(t) sint, то точка A колеблется вблизи точки отсчета в пределах отрезка [-1,1]. А если S(t) t2, то точка A

быстро удаляется от точки отсчета O в положительном направлении.

Говорят, что функция S(t) задает закон движения точки. Это означает, что зная функцию S(t) можно решить любую задачу, ка-

сающуюся ее движения. В частности, в любой момент времени t мы можем определить и измерить величину мгновенной скорости V(t) движущейся точки.

4

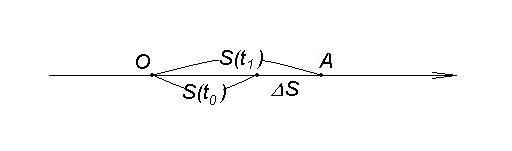
Рис 1.1

Приступая к решению этой задачи, будем предполагать, что скорость V(t) точки Aне является постоянной, но меняется плавно и постепенно.

Для нахождения V(t0) рассмотрим положения точки в момен-

ты времени t0 и t1, (см. Рис 1.1) и сравним приращение путиS S(t1) S(t0) с приращением времени t t1 t0. Величину

называют средней скоростью движения точки A на промежутке времени [t0,t1] (или средней скоростью изменения функции S(t)

на промежутке [t0,t1] изменения ее аргумента). При этом скорость в точках промежутка [t0,t1] не обязана совпадать со средней ско-

ростью.

Естественно предположить, что чем уже промежуток [t0,t1],

тем меньше успевает измениться скорость, и тем меньше мгновен-

ная скорость в точке t0 будет отличаться от средней скорости на узком промежутке [t0,t1]. То есть, мы получаем следующее опре-

деление.

Определение 1.1. Мгновенная скорость точки A в момент t0

есть предел средней скорости при условии, что длина отрезка [t0,t1] стремится к нулю:

5

Заметим, что начиная измерять что-либо, как правило, выбирают единицу измерения ― масштаб. В нашем случае за единицу измерения естественно принять скорость изменения самой независимой переменной t. Тогда, если S(t) t, то S t, средняя скорость на любом промежутке равна 1. Значит, мгновенная скорость движения, задаваемого законом S(t) t, также равна 1 при любом t.

Пример 1.2. (Задача об угловом коэффициенте касательной)

Пусть на линии выбрана некоторая точка M0 и пусть

M обозначает близкую к ней переменную точку. Прямая, проходящая через эти две точки называется секущей. Представим себе, что переменная точка M приближается к M0 . Тогда секущая M0M бу-

дет поворачиваться вокруг неподвижной точки M0 . Если секущая в процессе своего вращения будет приближаться к некоторой предельной прямой L, то эту прямую и называют касательной к кривой в точке M0 . Если же секущая не имеет предельного положе-

ния, то говорят, что в этом случае в точке M0 у кривой касатель-

ной нет.

Определение 1.2. Касательной к кривой в точке M0 назо-

вем прямую L, к которой приближается секущая M0M , когда точка M стремится к M0 , двигаясь вдоль линии (если предель-

ная прямая L существует).

Так как и касательная, и секущая проходят через общую точку M0 , то касательная L будет предельным положением секущей

M0M тогда и только тогда, когда угол между ними будет стре-

миться к нулю.

6

ка, а M M(x,y(x)) – переменная точка на графике функции.

Рис 1.2.

Обозначим через острый угол, на который надо повернуть ось OX вокруг точки О, чтобы она стала параллельна секущей M0M (со знаком +, если поворот происходит против часовой стрелки, и со знаком – , если поворот происходит по часовой стрелке). Из ска-

менного угла при M M0. Отсюда ясно, что если угол ост-

рый, то угловой коэффициент касательной kКАС tg удовлетворя-

ет равенству

Таким образом возникает следующее

7

Определение 1.3. Угловым коэффициент касательной к гра-

Сравнивая решения приведенных выше проблем, мы замечаем, что в обоих случаях ответ дается в виде предела отношения приращения функции к вызвавшему его приращению аргумента. Так как математика разрабатывает и изучает методы решения широких классов задач в абстрактной форме, отвлекаясь от их конкретного содержания, то вполне понятно, что этот предел становится предметом для ее рассмотрения в самой общей постановке. В результате были изучены свойства такого предела, найдены способы его быстрого нахождения и получены новые применения для решения как теоретических, так и практических задач.

§2. Определение производной функции в точке, ее физический и геометрический смысл

Пусть y f (x) ― произвольная функция, чья область опре-

деления содержит некоторый интервал (a,b) вместе с точкой

x0 (a,b). Пусть x (a,b) другая ― новая точка, отличная от x0.

Введем приращения x x x0, y f (x) f (x0), где из ново-

го значения соответствующей переменной вычитается ее старое значение.

Определение 2.1. Производной функции y f (x) в точке x0

называется число, обозначаемое y (x0) или f (x0) и равное

8

y

y (x0) f (x0) lim . (2.1)

x 0 x

Более подробно,

при условии, что предел отношения приращений существует.

Подчеркнем, что в определении производной сама функция должна быть определена как слева, так и справа от точки x0 и,

следовательно, приращение x, стремясь к нулю, может при-

нимать (и принимает) как положительные, так и отрицательные не равные нулю значения.

и, значит, отличается от этого числа на величину, стремящуюся к 0 вместе с x 0. Обозначим эту величину через ( x). Тогда

Формулы (2.2) и (2.3) понадобятся нам при рассмотрении понятий дифференциала и экстремума.

Если производная функции в точке существует, то функция называется дифференцируемой в этой точке, а само нахождение производной называется дифференцированием функции.

Замечание 2.1. Предел в определении производной предполагается либо конечным, либо определённого знака бесконечным. Ес-

9

ли f (x0) или f (x0) , то говорят о бесконечной производ-

ной.

В дальнейшем под производной, если не оговорено противное, будем понимать конечную производную.

Определение 2.1 и формулы (2.1), (2.1’) показывают, что производная f '(x0) в точке x0 является локальной характеристикой поведения функции вблизи этой точки и не зависит от значений функции за пределами любой как угодно малой, но фиксированной окрестности точки x0 .

Напомним, что функция y y(x) называется непрерывной в

точке x0, если lim y(x) y(x0). Если функция непрерывна в каж-

x x0

дой точке некоторого интервала, то ее график есть непрерывная кривая.

Задача 2.1. Докажите, что если функция дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное утверждение не верно, см. примеры ниже.

Физический смысл производной функции в точке

Напомним, что функция есть зависимая переменная, меняющаяся под управлением своего аргумента. Сравнивая определение понятия мгновенной скорости в примере 1 с определением производной функции в точке, приходим к выводу, что оба определения по сути совпадают. Значит:

производная в точке есть мгновенная скорость изменения функции, вызванная изменением ее аргумента и взятая относительно скорости изменения аргумента.

В этом состоит физический смысл производной функции в точке.

10