
Учебное пособие 1722
.pdf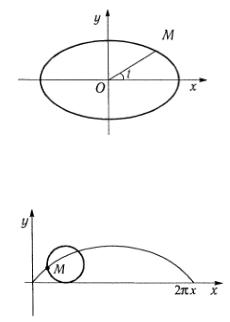
В параметрических уравнениях эллипса параметр t есть угол, образованный радиусом ОМ с осью абсцисс (рис. 3.66).
Рис. 3.66 3. Циклоидой называется кривая, описанная точкой М,
лежащей на окружности, если эта окружность катится без скольжения по прямой (рис. 3.67).
Рис. 3.67
Параметрические уравнения циклоиды: x = a (t −sin t ), y = a (1−cos t ), t [0, 2π]. При изменении t от 0 до 2π точка М опишет одну арку циклоиды.
9.1.Найти параметрические уравнения окружности
x2 + y2 = 2Rx, если полярная ось совпадает с осью Ох, а полюс
находится в начале координат.
Решение. Между декартовыми координатами и полярными существует зависимость x = ρ cosϕ, y = ρsinϕ. В
качестве |
параметра примем |
полярный угол ϕ = t, |
тогда |
уравнение |
окружности будет |
ρ = 2R cosϕ = 2R cos t. |
Если в |
формулы перехода вместо ρ и ϕ подставить их выражения в функции t , то получим
x = ρ(t )cos t = 2R cos2 t, y = ρ(t )sin t = 2R cos t sin t = R sin 2t. Откуда x = R (1+cos 2t ), y = R sin 2t.
161
9.2. Найти уравнения кривых в прямоугольных координатах:
a) x = −2 +t, y =1+2t; |
б) x = t2 +2t +4, y = t +1; |
в) x =1+2cos t, y = −3t +2sin t; |
г) x = a cos t, y = bsin t; |
д) x = 2R cos2 t, y = R sin 2t. |
|
Решение. a) Найдем из первого уравнения параметр t = x + 2 и исключим его из второго уравнения. Тогда получим
y =1+2(x + 2) или 2x − y +5 = 0 . Это уравнение прямой.
б) Представим первое уравнение в виде x = (t +1)2 +3,
тогда x = y2 +3. Это |
уравнение параболы с вершиной, |
||
смещенной на три единицы по оси Ох. |
|
||
в) Разрешим |
уравнения |
относительно |
|
тригонометрических |
функций |
2cos t = x −1, 2sin t = y +3. |
|
Возведем в квадрат и |
сложим |
4 = (x −1)2 +(y +3)2 . Кривая |
|
предсталяет окружность с центром в точке (1; -3) и радиусом равным 2.
|
|
|
|
|
г) Разделим правые части из, а и b, возведем выражения |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
y |
2 |
|
2 |
t +sin |
2 |
t |
|
|
||||||||||
в |
квадрат |
и |
сложим |
|
|
|
|
+ |
|
|
|
= cos |
|
|
|
или |
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x2 |
+ |
y2 |
=1. |
|
Это уравнение эллипса. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
a2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
д) Возведем второе выражение в квадрат и преобразуем |
|||||||||||||||||||||||||||||
|
y2 |
= R2 sin2 |
|
|
|
|
|
( |
|
|
|
|
) |
cos2 t. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2t y2 = 4R2 1−cos2 t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Найдем из первого уравнения cos2 t = |
x |
|
|
- и подставим, тогда |
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
2R |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
2 |
(x − R) |
2 |
|
|
2 |
2 |
|
|||||||||
|
|
y |
|
= 4R |
|
1− |
|
|
|
y |
|
= 2Rx − x |
|
|
|
+ y |
|
|
= R |
. |
||||||||||||||
|
|
|
|
|
2R |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение окружности с центром, смещенным по оси Ох на радис R.
162
4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 4.1. Системы координат
1°. Декартова или прямоугольня система координат представляет совокупность трех взаимно-перпендиулярных осей: оси абсцисс 0x , оси ординат 0 y и оси аппликат 0z .
Система координат называется правой, если для каждой пары осей ху, yz, zx кратчайший поворот первой из них вокруг начала координат до совпадения с положительным направлением второй виден со стороны положительного направления третьей оси, совершающимся против часовой стрелки, и левой - в противоположном случае.
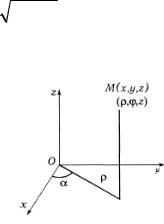
Декартовыми координатами точки М называются проекции радиус-вектора ОМ (рис. 4.1) на оси координат.
2°. Цилиндрическими координатами точки М являются ее апликата z и полярные координаты проекции точки М на плоскость y0x (рис. 4.1).
Цилиндрические |
координаты |
связаны |
с |
прямоугольными координатами формулами (3) |
|
|
|
x = p cosϕ; |
y = p sinϕ; z = z . |
|
(1) |
Из равенств (1) легко находятся формулы обратного перехода
p = x2 + y2 ; tgϕ = |
y |
|
; |
z = z |
(2) |
|
x |
||||||
|
|
|
|
|||
причем выбор нужного угла ϕ из |
|
двух главных |
значений |
|||
можно произвести, например, по знаку координаты у.
Рис. 4.1 163
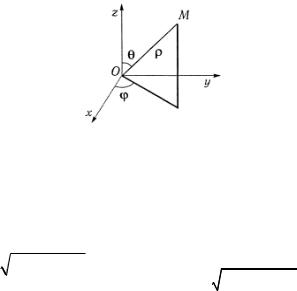
3°. В сферической системе координат (рис. 4.2) положение точки М определяется: ее расстоянием p от начала
координат (радиус-вектором) (0 ≤ p < ∞); углом ϕ , который образует проекция радиус-вектора на плоскость x0 y с положительным направлением оси 0x (0 ≤ϕ < 2π )θ , который
радиус-вектор образует с положительным направлением оси
0z (0 ≤θ <π ).
Рис. 4.2
Связь между прямоугольными координатами точки и ее сферическими координатами устанавливается формулами
x = p sinθ cosϕ; |
y = p sinθ sinϕ; |
z = p cosθ . |
|
(3) |
||
Решая уравнения |
(3) относительно p,ϕ,θ, |
получим |
||||
формулы обратного перехода |
|
|
|
|||
p = x2 + y2 + z2 ; tgϕ = |
y |
; cosθ = |
z |
, |
(4) |
|
|
x2 + y2 + z2 |
|||||
|
|
x |
|
|
||
причем выбор нужного знака угла ϕ из двух главных значений можно произвести, например, по знаку координаты y .
4.2. Плоскость
1°. Основные уравнения плоскости.
1. Общее уравнение плоскости. Всякая плоскость определяется уравнением первой степени с тремя неизвестными
Ax + By +Cz + D = 0 . |
(1) |
2. Нормальное уравнение плоскости
164
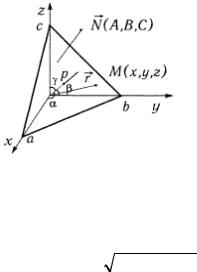
r n°− p = 0 или x cosα + y cos β +cosγ − p = 0 , |
(2) |
где p -длина перпендикуляра, опущенного на плоскость из начала координат; α, β,γ - углы, которые этот перпендикуляр
образует с положительными направлениями координатных осей; n° - единичный вектор направления ОР (рис. 4.3).
Рис. 4.3
Для приведения общего уравнения плоскости (1) к нормальному виду нужно это уравнение умножить на
нормирующий множитель M = |
1 |
, при этом знак |
± A2 + B2 +C2 |
нормирующего множителя должен быть противоположен знаку D в уравнении (1). (Если D = 0, то знак М может быть любой). Зная общее уравнение плоскости, косинусы направляющих углов в нормальном уравнении плоскости находятся по формулам
cosα = A M ; |
cos β = B M ; |
cosγ = C M , |
|||||||||
а длина перпендикуляра p = |
|
D M |
|
. |
|
||||||
|
|
|
|||||||||
3. Уравнение плоскости в отрезках на осях |
|||||||||||
|
x |
+ |
y |
+ |
z |
=1, |
(3) |
||||
|
|
b |
|
||||||||
|
a |
|
c |
|
|||||||
где a,b, c - отрезки, которые |
отсекает плоскость на |
||||||||||
координатных осях (Рис. 4.3). |
|
||||||||||
|
|
|
|
165 |
|
|
|
||||

4. Уравнение плоскости, проходящей через данную |
|
точку M1 (x1, y1, z1 ) и перпендикулярной данному |
вектору |
NG (A, B,C ) |
|
A(x − x1 )+ B (y − y1 )+C (z − z1 )= 0 . |
(4) |
5. Параметрические уравнения плоскости |
|
x = x0 +uax +vbx ; |
|
y = y0 +uay +vby ; |
(5) |
|
z = z0 +uaz +vbz , |
|
|
|
|
где |
u, v - два параметра; ax ,bx , ay ,by , az ,bz |
- проекции векторов |
|||
G |
G |
|
G |
G |
G |
a иb удовлетворяющих векторному произведению |
a |
×b |
= N . |
||
2°. Основные задачи на плоскость.
1.Точка пересечения трех плоскостей находится из совместного решения их уравнений.
2.Уравнение плоскости, проходящей через три точки
M1 (x1, y1, z1 ), M2 (x2 , y2 , z2 ), M3 (x3 , y3 , z3 )
x − x1 x2 − x1 x3 − x1
y − y1 y2 − y1 y3 − y1
z − z1
z2 − z1 = 0 . (6) z3 − z1
3. Параметрические уравнения плоскости, проходящей через три точки, имеют вид
x = x1 +u (x2 − x1 )+v (x3 − x1 ); |
|
y = y1 +u (y2 − y1 )+v (y3 − y1 ); |
(7) |
z= z1 +u (z2 − z1 )+v (z3 − z1 ).
4.Угол между двумя плоскостями равенG углу между нормальными к ним векторами N1 (A1, B1,C1 )иN 2 (A2 , B2 ,C2 )
166
cosϕ = |
|
NG1 NG2 |
= ± |
|
A1 A2 + B1B2 +C1C2 |
|
. (8) |
||||||||
|
NG1 |
|
|
|
NG2 |
|
|
|
|
|
|
|
|||
|
A2 |
+ B2 |
+C2 |
A2 |
+ B2 |
+C2 |
|||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
|
5. Если две плоскости взаимно-перпендиклярны, то сумма произведений коэффициентов при одноименных
текущих координатах равна нулю |
|
A1 A2 + B1B2 +C1C2 = 0 . |
(9) |
6. Если две плоскости параллельны, то коэффициенты при одноименных текущих координатах пропорциональны
A1 = B1 = C1 . (10)
A2 B2 C2
7. Расстояние от точки M1 (x1, y1, z1 ) до плоскости
d = |
|
x cosα + y cos β + z cosγ − p |
|
= |
|
Ax1 + By1 +Cz1 + D |
|
. (11) |
|||
|
|
||||||||||
|
|
|
|||||||||
|
|
1 |
1 |
1 |
|
|
|
± A2 |
+ B2 +C2 |
|
|
|
|
|
|
|
|
|
|
|
|||
2.1. |
Дано |
уравнение плоскости |
9x −2 y +6z −11 = 0. |
||||||||
Привести: а) к нормальному виду; б) к уравнению плоскости в отрезках на осях.
|
|
|
Решение. |
а) |
|
|
|
Найдем нормирующий |
множитель |
||||||||||||||||||
M = |
|
|
1 |
|
|
|
|
|
|
= |
1 |
|
. |
Умножая на М данное уравнение, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
92 +(−2)2 +62 |
11 |
|
|
|
|
|
||||||||||||||||||
получим |
|
9 |
|
|
x − |
2 |
|
y + |
|
6 |
|
z −1 = 0, |
|
|
|||||||||||||
11 |
|
|
11 |
|
|
||||||||||||||||||||||
|
|
|
|
9 |
11 |
|
|
|
2 |
|
6 |
|
|
|
|||||||||||||
где cosα = |
|
, cos β = − |
, cosγ = |
и p =1. |
|
|
|||||||||||||||||||||
|
|
|
11 |
|
|
|
|||||||||||||||||||||
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|||||||||
б) Перенесем свободный член в правую часть уравнения и |
|||||||||||||||||||||||||||
разделим на него уравнение, представив его в виде |
|
|
|||||||||||||||||||||||||
|
x |
+ |
|
y |
|
+ |
|
z |
=1. |
|
Отрезки на осях a = 11, b = − |
11, c = |
11. |
||||||||||||||
11 |
−11 |
|
11 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
2 |
6 |
|||||||||||
9 |
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
167 |
|
|
|
|

2.2. Написать общее и параметрические уравнения плоскости, проходящей через три точки
A(1,1, 0); B (3, 2, −1)иC (2, −1, 4).
Решение. Воспользуемся уравнением (6)
x −1 |
y −1 |
z |
|
|
|
||||
2 |
1 |
−1 |
|
= 0. |
1 |
−1 |
4 |
|
|
Общее уравнение искомой плоскости 2x - 9 y - 5z +7 = 0.
Для получения параметрических уравнений плоскости подставляем координаты точек в формулы (7)
x=1+2u +v,
y=1+u −2v, z = −u +4v.
2.3.Через точку (2,1,3) провести плоскость, которая
была бы перпендикулярна к плоскости x +3y - z +2 = 0 и
проходила бы через точку (3,-1,5).
Решение. Воспользуемся уравнением плоскости (4), проходящей через данную точку и перпендикулярной
некоторому вектору N (A, B,C )
A(x −2)+ B (y −1)+C (z −3)= 0. (*)
Из условия перпендикулярности (9) этой и данной плоскости имеем A +3B −C = 0.
Поскольку наша плоскость должна проходить через точку (3,-1,5), то подставляя ее координаты в уравнение (*), получим A −2B +2C = 0.
Мы получили систему трех линейных однородных уравнений относительно неизвестных А, В, С. Чтобы система имела решение отличное от нулевого, необходимо и достаточно, чтобы определитель равнялся нулю
168

x −2 |
y −1 |
z −3 |
|
|
|
||||
1 |
3 |
−1 |
|
= 0. |
1 |
−2 |
2 |
|
|
Отсюда уравнение искомой плоскости 4x - 3y - 5z +10 = 0.
2.4. Написать уравнение плоскости, проходящей через
точку M0 (2,1, −2) |
перпендикулярную |
линии |
пересечения |
|||||||
плоскостей x +3y +2z +1 = 0 и 3x +2 y − z +8 = 0. |
|
|||||||||
Решение. Найдем вектор параллельный линии |
||||||||||
пересечения плоскостей |
|
iG Gj |
|
|
|
|
|
|||
G |
G |
G |
|
k |
|
G |
G |
G |
||
N |
= N1 |
×N2 |
= |
1 3 2 |
= −7i +7 j − |
7k. |
||||
|
|
|
|
3 |
2 |
−1 |
|
|
|
|
Воспользуемся |
теперь |
уравнением |
плоскости, |
|||||||
проходящей через точку M0 , |
нормальный |
вектор которой |
||||||||
параллелен линии пересечения плоскостей |
|
|
||||||||
−7 (x −2)+7 (y −1)−7 (z + 2)= 0 или x − y + z +1 = 0 |
||||||||||
2.5. Через точку (2,-1,3) провести плоскость, |
||||||||||
параллельную плоскости x - 2 y |
+ 4z - 5 = 0. |
|
|
|||||||
Решение. Уравнение плоскости, проходящей через данную точку, имеет вид A(x - 2) + B( y +1) +C(z - 3) = 0.
Поскольку плоскости параллельны, то, используя условие параллельности плоскостей (10), подставляем вместо А, В, С значения коэффициентов из заданного уравнения плоскости (с коэффициентом пропорциональности, равным 1)
x −2 −2(y +1)+4(z −3)= 0
или x −2 y +4z −16 = 0.
2.6. Вычислить расстояние от точки М (2;-1;3) до плоскости 11x −2 y +10z +6 = 0.
Решение. По формуле (10) имеем
169
d = |
|
11 2 −2(−1)+10 3 +6 |
|
= 60 |
= 4. |
|
|
|||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
(11)2 +(−2)2 +(10)2 |
|
|
15 |
|
|
|
|
|||||||
2.7. Составить уравнение плоскости, проходящей через |
||||||||||||||||||
точку M1 (1; −1; 2) |
и перпендикулярной вектору N (4;3; −1). |
|||||||||||||||||
Решение. |
В |
соответствии |
с |
|
|
уравнением |
(5) |
имеем |
||||||||||
4(x -1) +3( y +1) - (z - 2) = 0, откуда 4x +3y - z +1 = 0. |
|
|
||||||||||||||||
2.8. Вычислить угол между плоскостями |
|
|
||||||||||||||||
x +2 y −3z −4 = 0; 2x - y + z +l = 0. |
|
|
||||||||||||||||
Решение. Используя формулу (7), получим |
|
|
||||||||||||||||
|
|
|
|
|
1 2 +2 |
( |
−1 + |
( |
−3 |
) |
1 |
|
|
3 |
|
|||
cosϕ = |
|
|
|
|
|
) |
|
|
|
= − |
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 21 |
|||||
|
|
12 +22 +(−3)2 |
22 +(−1)2 +(1)2 |
|
||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда ϕ = arccos − |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Следует отметить, что в данном случае получен тупой угол. Острый угол между этими плоскостями равен π −ϕ,
2.9. Найти расстояние между параллельными плоскостями
5x +2 y −3z −7 = 0 и 5x +2 y −3z +4 = 0.
Решение. Искомое расстояние равно расстоянию от любой точки, лежащей на одной из плоскостей, до другой. Возьмем на первой плоскости точку, полагая для удобства расчета
x = 0; y = 0 . Тогда |
z = |
7 |
. |
|
0;0; − |
7 |
|
3 |
Расстояние от точки М |
3 |
|
||||
|
|
|
|
|
|
||
до второй плоскости находим по формуле (11) |
|
||||||
d = |
|
5 0 +2 0 −3(−7 |
3 )+ 4 |
|
= |
11 |
. |
|
|
||||||
|
|
|
|
|
|||
|
|
|
|
38 |
|||
25 +4 +9 |
|
|
|
|
|||
170
