Гидрогазодинамика. методические указания к лабораторным работам для студентов направления подготовки 20.03.01 «Техносферная безопасность». Скоморохов Г.И., Шматов Д.П

выполнения работы и обработки опытных данных

1) Открыть компьютерную версию лаборатории для имитационного выполнения лабораторных работ при изучении дисциплин «Гидравлика». Включить виртуальную установку для экспериментального исследования режимов движения жидкости.

2) Установить минимальное значение А открытия крана 4 на стеклянной трубе 2. Ви-

4) Увеличивая расход воды, последовательно провести опыты для восьми - десяти (8 - 10) значений А открытия крана 4.

5) Обработать экспериментальные данные и произвести необходимые вычисления. 6) Построить= ( ) график зависимости гидравлических потерь от средней скорости тече-

ния воды . По графику определить критическую скорость υкр, а через неё и значе-

ние критического числа Рейнольдса - Råêð = υêðν d . 7) Дать заключение по результатам работы.

Контрольные вопросы

1.Назовите режимы движения жидкости и укажите их характерные особенности.

2.Что такое критерий Рейнольдса, факторы, от которых он зависит.

3.Что такое критическое число Рейнольдса?

21

4.С какой целью и каким образом при гидравлических расчётах определяют режим движения жидкости?

5.Что такое критическая скорость, от каких факторов она зависит и как её определяют?

6.Напишите и поясните аналитические зависимости потерь напора по длине от средней скорости потока при ламинарном и турбулентном режимах движения жидкости.

7.Изобразите график зависимости потерь напора по длине от средней скорости (в логарифмических координатах) и дайте пояснения к нему.

Лабораторная работа № 4 Изучение гидравлических сопротивлений напорного трубопровода

с определением коэффициентов трения и коэффициентов местных сопротивлений

Цель работы:

1) Определить по опытным данным, воспользовавшись формулами (4.1) и (4,5), значение коэффициента гидравлического трения λ и величины коэффициента ζ для трех видов местных сопротивлений;

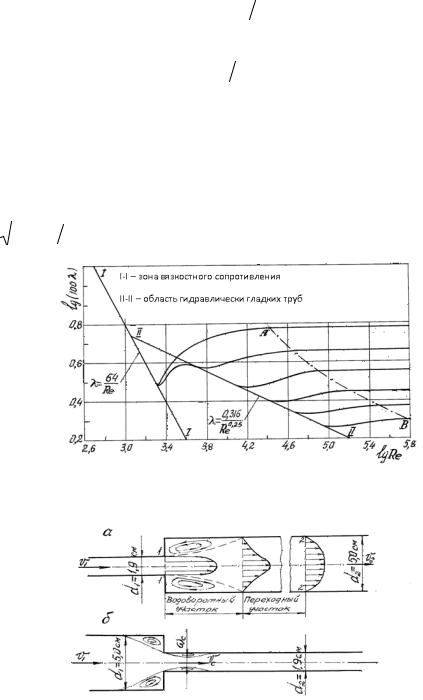
2)Установить, воспользовавшись соотношениями А.Н. Альтшуля или же графиком Никурадзе (см. рис. 4.1) области гидравлического сопротивления, в которых работали участки напорного трубопровода;

3)Вычислить значения коэффициентов гидравлического трения λ по соответствующим эмпирическим формулам;

4)Вычислить справочные значения коэффициентов местных сопротивлений по фор-

мулам – ζ рр и ζ р.с. ; 5) Оценить сходимость λоп и ζоп с их расчетными справочными значениями.

Краткие теоретические сведения

Экспериментальными исследованиями установлено, что при движении жидкости часть полного напора (энергии) затрачивается на преодоление работы вязкостных и инерционных сил, т.е. возникают потери напора.

При равномерном движении жидкости гидравлическое сопротивление, проявляющееся равномерно по всей длине потока, называют сопротивлением по длине, а вызываемые им

потери напора, – потерями напора по длине he . Эти потери в круглых трубопроводах вычисляют по формуле Дарси-Вейсбаха:

где λ – безразмерный коэффициент, называемый коэффициентом гидравлического трения

(коэффициентом Дарси). Величина коэффициента λ характеризует гидравлическое сопротивление трубопровода и зависит в общем случае от числа Рейнольдса Re и относительной

шероховатости ∆э/d трубопровода, т.е. λ=f(Rе, ∆э/d);

l, d – длина и внутренний диаметр трубопровода; υ – средняя скорость движения потока жидкости.

Величину коэффициента λ при гидравлических экспериментах вычисляют по опытным данным из формулы (4.1). При гидравлических же расчетах – по эмпирическим и полуэмпирическим формулам, например:

22

справочной литературы в зависимости от материала трубопровода и состояния его внутренней поверхности. Например, для труб из органического стекла ∆э=0,006 мм, а для стальных водопроводных труб ∆э=0,20…0,50 мм.

Область гидравлического сопротивления при расчетах определяют или непосредст-

венно по графикам λ=f(Re,∆э/d), полученным опытным путем для труб из различных материалов и приведенным в справочной литературе, например, по графику Никурадзе (рис. 3.1),

или же с помощью соотношений 10d и 500d , предложенных А. Д. Альтшулем на основе

∆э ∆э

использования упомянутых графиков. В последнем случае поступают следующим образом. Вычисляют соотношения 10d/∆э и 500d/∆э и сравнивают их с числом Рейнольдса Re =

Vd/ν. При этом, если, Re ≥ 500∆эdэ , трубопровод работает в области гидравлически глад-

ких труб. Если Re ≤10∆эd , трубопровод работает в области квадратичного сопротивле-

ния. Если же 10d/∆э < Re > 500dэ/∆э, трубопровод работает в области доквадратичного со-

противления:

Следует иметь в виду, что для каждой области гидравлического сопротивления предложены и используются при гидравлических расчетах свои формулы для вычисления коэф-

фициента λ.

Местные сопротивления. Другой вид гидравлических сопротивлений, возникающих в местах резкого изменения конфигурации потока, называют местным сопротивлениями, а вызываемые ими потери напора, – местными потерями напора (hм).

При прохождении через любое местное сопротивление поток жидкости деформируется (рис. 3.2 а,б), вследствии чего движение становится неравномерным резко изменяющимся, для которого характерны:

а) значительное искривления линий потока и кривых сечений потока; б) отрывы транзитной струи от стенок трубопровода; в) повышенная пульсация скоростей и давлений; г) изменение формы эпюр скоростей.

Местные потери напора расчетах вычисляют по формуле Вейсбаха:

где ζ – коэффициентом местного сопротивления (безразмерный);

υ– средняя скорость потока в сечении за местным сопротивлением.

Величина коэффициента ζ зависит в общем случае от конфигурации, т.е. от формы проточной части местного сопротивления и числа Рейнольдса.

23

Величину ζ для каждого вида местного сопротивления определяют по данным гидравлических экспериментов, пользуясь формулой (4.5). Полученные таким образом значения коэффициентов ζ для различных видов местных сопротивлений приводятся в справочной литературе. Исключением является резкое расширение и резкое сужение трубопровода (см. рис. 4.2 а, б), для которых численные значения координаты ζ определяются по формулам, полученным теоретически. Так, при резком расширении трубопровода, когда средняя ско-

Рисунок 4.1 – График зависимости коэффициента гидравлического трения λ от числа Re (график Никурадзе)

Рисунок 4.2 – Схемы движения жидкости при резком изменении сечения трубопровода: а) резкое расширение трубопровода; б) резкое сужение трубопровода

24

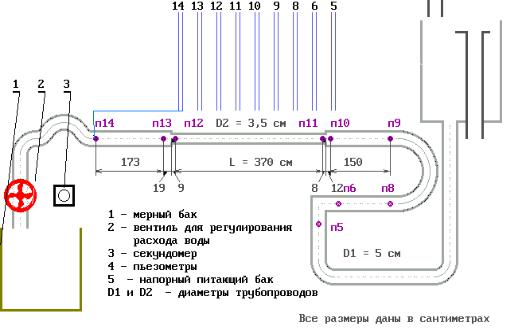
Описание установки. Установка (рис. 4.3) представляет собой систему напорных трубопроводов с последовательно расположенными на нем гидравлическими сопротивлениями (по длине и местными). К каждому гидравлическому сопротивлению подключено по два пьезометра (перед и за ним). Все пьезометры для удобства работы выведены на щит 4. Для регулирования расхода воды Q в системе служит вентиль 2. Величина Q измеряется с

помощью мерного бака 1 и секундомера. 3. Подача воды в систему осуществляется из питающего резервуара 5 по трубе 7 открытием задвижки 6. Постоянный уровень воды в резервуаре 5 ( для обеспечения установившегося движения в системе) поддерживается переливным устройством. Вода в резервуар 5 подается центробежным насосом.

Рисунок 4.3 – Схема экспериментальной установки для исследования гидравлических сопротивлений

Порядок выполнения работы и обработки опытных данных

При закрытом вентиле 2 и задвижке 6 включить насос и обеспечить подачу воды в питающий резервуар 5. После наполнения водой резервуара и стабилизации уровня воды в нем (переливное устройство должно при этом работать) следует плавным открытием вентиля 2 подать воду в систему трубопроводов. Далее, необходимо измерить: отметки уровней воды в пьезометрах, расход воды в системе (с помощью мерного бака 1 и секундомера 3), а так же ее температуру (термометром в резервуаре 1). Результаты измерений для двух опытов (при разных расходах воды) записать в таблицу4.1.

Обработать опытные данные и результаты представить в виде таблицы 4.1. Сформулировать выводы по результатам работы.

Контрольные вопросы

1.Напишите и поясните формулы Дарси-Вейсбаха и Вейсбаха.

2.Как опытным путем определяют величины коэффициентов λ и ξ.

3.Что характеризуют коэффициенты λ и ξ, от каких факторов в общем случае они зависят и как их определяют при гидравлических расчетах?

4.Объясните, что такое ∆э и ∆э/d, как найти величину ∆э при гидравлических расчетах.

5.Назовите области гидравлического сопротивления трубопроводов и объясните, как

25

определяют область сопротивления при гидравлических расчетах.

6. Изобразите схемы движения жидкости при резком повороте трубы на 900, а также при резком расширении и резком сужении трубопровода и дайте пояснения к ним, указав, что характерно для движения потока при протекании его через любое местное сопротивление.

Таблица 4.1 – Протокол результатов измерений и вычислений

26

Лабораторная работа № 5 Истечение жидкости через малые отверстия в тонкой стенке

и насадки в атмосферу при постоянном напоре

Цель работы:

1. Определить по опытным данным величины коэффициентов: µоп, ϕоп, εоп, ζоп, при истечении через малое круглое отверстие диаметром d=2 см при постоянном напоре в атмо-

сферу и величины коэффициентов µНоп = ϕНоп = ζНоп для внешнего цилиндрического и конических (сходящегося и расходящегося) насадков при Н= Сonst в атмосферу.

2. Сравнить значения коэффициентов, полученные в опытах, со справочными и подсчитать относительные отклонения.

Краткие теоретические сведения

Отверстие считается малым, если его вертикальный размер не превышает 0,1 глубины погружения отверстия под уровень сосуда, из которого происходит истечение жидкости. Стенка считается тонкой, если вытекающая струя соприкасается лишь с внутренней кромкой стенки и не касается боковой поверхности отверстия.

Если в боковой стенке сосуда с жидкостью на глубинеH под уровнем имеется круглое от-

верстие диаметромd и площадьюω, то вытекающая струя претерпевает сжатие (рис. 5.1). Движение струи в сжатом сечении близко к параллельно-струйному. На некотором рас-

стоянии от отверстия, близком к 0,5d, вытекающая струя получает сжатие поперечного сечения,

имеет равное сжатие по всему периметру, то сжатие называется полным, в противном случае сжатие называется неполным. Сжатие также может быть совершенным и несовершенным. Совершенным сжатием называется такое, при котором ни свободная поверхность, ни близлежащие стенки не влияют на сжатие струи. Это будет в том случае, если размер отверстия в 3 раза меньше расстояния до ближайшей стенки резервуара или свободной поверхности.

27

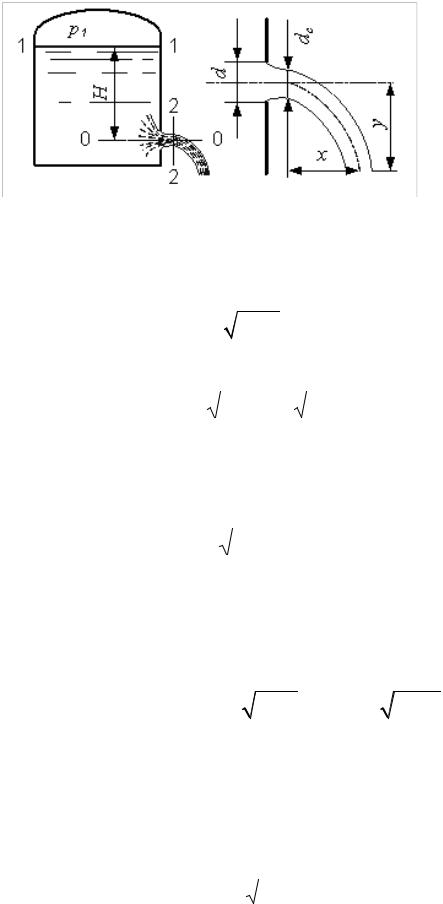
Рисунок 5.1 – Истечение жидкости из малого отверстия в тонкой стенке

Среднюю скорость струи сжатом сечении 2-2 при 0 = вычисляют по формуле, полученной из уравнения Д. Бернулли, составленного для сечений I-I и 2-2 (см. рис. 5.1):

где α – коэффициент Кориолиса;

ζ – коэффициент сопротивления отверстия.

На основе использования уравнения траектории струи, вытекающей из отверстия,

В формуле (5.5) xi и yi координаты произвольно взятой точки траектории струи. При истечении из отверстия во внимание принимают только местные потери напо-

ра, поскольку напор теряется главным образом вблизи отверстия, где скорости достаточно велики.

Расход жидкости Q через отверстие равен:

Здесь µ коэффициент расхода отверстия, учитывающий влияние гидравлического сопротивления и сжатия струи на расход жидкости. С учетом выражения для µ формула (1.25) принимает вид:

28

Величины коэффициентов ε, ζ, ϕ, µ для отверстий определяют опытным путем. Установлено, что они зависят от формы отверстия и числа Рейнольдса. Однако при больших

Истечение жидкости через насадки 2,5 ≤ ≤ 5

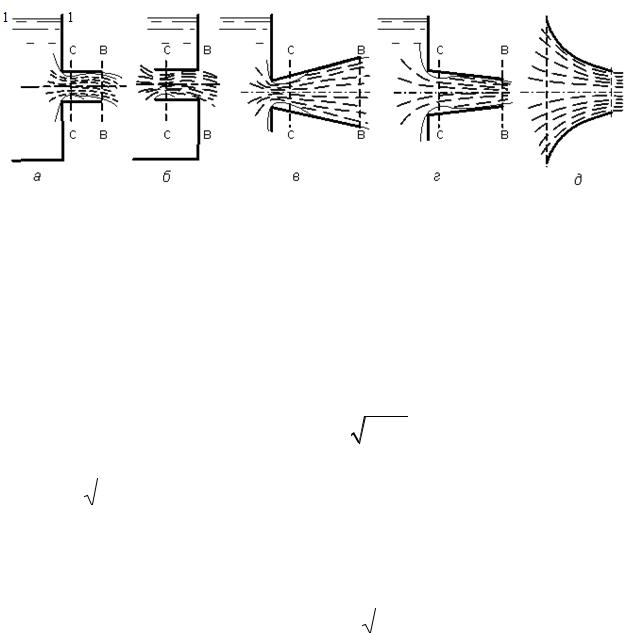
Насадкой называют патрубок длиной н (рис.5.2), присоединенный к малому отверстию в тонкой стенке с целью изменения гидравлических характеристик истечения (скорости, расхода жидкости, траектории струи).

Насадки бывают цилиндрические (внешние и внутренние), конические (сходящиеся и расходящиеся) и коноидальные, т.е. очерченные по форме струи, вытекающей из отверстия

(рис. 5.2).

Рисунок 5.2 – Виды насадков: а – внешний цилиндрический;

б– внутренний цилиндрический; в – конический расходящийся;

г– конический сходящийся; д – коноидальный

Использование насадки любого типа вызывает увеличение расхода жидкости благодаря вакууму, возникающему внутри насадка в области сжатого сечения с-с (см.рис. 5.2) и

29

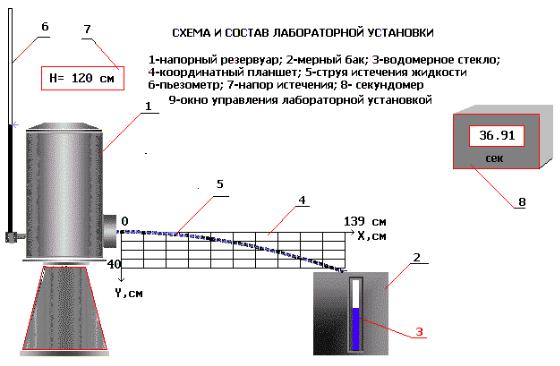
Описание установки. Установка (рис. 5.3) представляет собой напорный резервуар 1, в боковой поверхности которого имеется отверстие, закрываемое рычажным клапаном 3. Перед отверстием смонтирован поворотный круг 10 с отверстиями различной формы и насадками различных типов. Поворачивая круг, можно установить против отверстия насадок нужного типа или отверстие требуемой формы. Постоянный уровень воды в резервуаре 1 во время опытов поддерживается переливной трубой II.

Для определения напора истечения Н резервуар I снабжен водомерной трубкой 6 со шкалой, нуль которой совмещен с центром отверстия.

Расход воды при истечении из отверстий и насадков измеряется с помощью передвижного мерного бака 2 и секундомера 8. Координаты X и Y произвольных точек траектории струи измеряются с помощью координатной сетки, нанесенной на поворачивающийся щит 4.

Рисунок 5.3 – Схема экспериментальной установки для исследования истечения жидкости

Порядок выполнения работы и обработки опытных данных

1.Открыть задвижку, заполнить водой резервуар.

2.Поворотом круга установить перед отверстием круглое отверстие диаметром d=2 см и закрепить круг в этом положении.

3.Открыть клапан 3 и обеспечить с помощью задвижки 15 истечение воды при по-

стоянном напоре Н, измерить его, а также координаты Xk и Yk произвольно выбранной точки “к” траектории струи.

4.Измерить расход воды Q с помощью бака 5 и секундомера (измеряемый объем воды должен быть не менее 50 литров).

5.Результаты измерений записать в графу 4 таблицы 5.1.

6.Закрыть клапаном 3 отверстие 9 и опорожнить вентилем 8 мерный бак

7.Устанавливая с помощью поворотного круга 10 против отверстия 9 поочередно внешний цилиндрический и конические (сходящийся и расходящийся) насадки, измерить для каждого из них расход воды Q и напор Н (последний должен поддерживаться в опытах постоянным и равным напору при истечении из круглого отверстия).

30