
Методические указания к выполнению лабораторной работы по дисциплине «Методы пассивной радиолокации». Дубыкин В.П
.pdf
ФГБОУ ВО «Воронежский государственный технический университет»
Кафедра радиотехники
29-2018
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению лабораторной работы по дисциплине «Методы пассивной радиолокации» для студентов направления 11.04.01 «Радиотехника» (магистерская программа «Радиотехнические средства обработки и защиты информации в каналах связи») очной формы обучения
Воронеж 2018
УДК 621.396.96(07) ББК 32.95я7
Составитель канд. техн. наук, доц В.П. Дубыкин
Методические указания к выполнению лабораторной
работы по дисциплине «Методы пассивной радиолокации» для студентов направления 11.04.01 «Радиотехника» (магистерская программа «Радиотехнические средства обработки и защиты
информации в каналах связи») очной формы обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост. В.П. Дубыкин. Воронеж, 2018. 13 с.
Методические указания содержат описание принципов построения и функционирования пассивных многопозиционных радиолокационных систем и относятся к дисциплине «Методы пассивной радиолокации», разделу «Методы определения
координат источников радиоизлучения в угломерных систе-
мах». Выполнение лабораторной работы предполагается при помощи методов имитационного моделирования с проверкой получаемых результатов практическими расчетами.
Табл. 1 . Ил. 1 . Библиогр.: 5 назв.
Рисунок на обложке В.П. Дубыкина
УДК 621.396.96(07) ББК 32.95я7
Рецензент канд. техн. наук, доц. В.П. Литвиненко
Печатается по решению учебно-методического совета ВГТУ
© ФГБОУ ВО «Воронежский государственный технический университет», 2018
ОБЩЕЕ ОПИСАНИЕ МЕТОДОВ
Методы пассивной радиолокации, обладая общностью с методами активной, имеют свои специфические особенности. Из-за отсутствия информации о начале времени излучения дальность до источника радиоизлучений (ИРИ) не может быть определена по данным приема радиосигналов только в одной приемной позиции (ПП). Поэтому для определения координат ИРИ требуется использование двух или нескольких ПП, соединенных каналами радиосвязи.
При этом отсутствие передающих устройств в системах пассивной радиолокации упрощает аппаратуру и повышает скрытность работы систем.
В настоящее время известны и широко используются следующие методы:
1.Угломерный метод, основанный на измерениях угловых направлений на ИРИ в двух и более ПП, разнесенных на некоторое расстояние между собой, называемое базой. Если ИРИ расположен в горизонтальной плоскости, то достаточно измерить два азимутальных направления. В этом случае место положения ИРИ (координаты на плоскости х, у) определяется точкой пересечения двух прямых (пеленгов), каждая из которых является линией положения, то есть геометрическим местом точек возможного местонахождения ИРИ;
2.Разностно-дальномерный метод, основанный на изменении взаимных задержек в распространении радиосигнала от ИРИ до двух ПП, объединенных одной базой. При этом приемные позиции являются фокусами гипербол, на которых располагаются ИРИ. Поэтому линиями положения являются гиперболы, а местоположение ИРИ определяется точкой пересечения гипербол;
1
3. Угломерно-разностно-дальномерный метод основан на совместном использовании угломерного и разностнодальномерного метода, когда в качестве линий положения ИРИ рассматриваются как пеленги, так и гиперболы, а координаты ИРИ определяются точками пересечения пеленгов и гипербол.
В данной работе решение задачи определения координат ИРИ рассматривается на плоскости с использованием правой прямоугольной системы координат хОу, в которой азимутальные углы (пеленги) отсчитываются относительно оси абсцисс против хода часовой стрелки.
УГЛОМЕРНАЯ СИСТЕМА
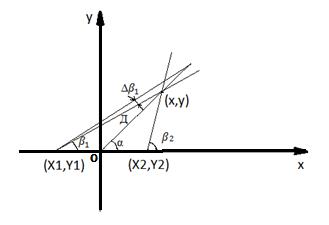
Геометрия построения рассматриваемой угломерной системы (УС), реализующей угломерный метод, представлена на рисунке.
Структура угломерной системы
2
Пусть ПП системы и ИРИ расположены в плоскости хОу так, как показано на рис. 1. Положение m-ой ПП (пеленгатора)
характеризуется координатами , (m=̅̅̅̅), а истинное положение ИРИкоординатами х,у. В каждой ПП (независимо от других позиций) измеряются угловые направления (пеленги ), которые вследствие ошибок пеленгования отличаются от истинных значений на углы ∆ - ошибки пеленгования. В следствии неизбежного наличия этих ошибок нельзя точно определить положение координат ИРИ (х,у) а можно лишь говорить о послеопытной плотности вероятности нахождения ИРИ в некоторой области, тем резче очерченной, чем точнее измеряются пеленги . Зная эту плотность, и максимизируя ее в области нахождения ИРИ по методу максимального правдоподобия, можно определить оптимальные оценки координат
ИРИ и оценить потенциальную точность их измерений [1]. Считая измерения каждого пеленгатора независимыми от
других измерений и используя теорему умножения [2], послеопытную плотность вероятности координат запишем в виде:
, (1)
где –нормирующий множитель, - измеренные пеленги.
Предполагая ошибки пеленгования случайными и независимыми, а закон их распределения нормальным, запишем:
∏ |
|
|
|
( |
|
) |
√ |
|
|
|
|||
|
-дисперсия ошибки измерения m- го пеленга М-число приемных позиций УС.
3

Из формулы (2) следует, что ошибки связаны с координатами (х,у) ИРИ сложными нелинейными функциональными соотношениями. Считая, что ошибки измерения координат ИРИ являются малыми и, осуществляя линеаризацию
функциональных соотношений |
(х,у), можем записать: |
|
||
(х,у)= |
|
|
, |
(3) |
|
|
|||
где |
– расстояние от ИРИ |
|||
до m-ой приемной позиции (пеленгатора).
Подставляя (2), (3) в (1), послеопытную плотность вероятности координат ИРИ запишем:
= |
{ |
|
∑ |
|
} (4) |
|
|
где С-нормирующий множитель.
Для продолжения исследований выражения (4) на максимум преобразуем его соотношения в фигурных скобках к виду квадратичной формы:
λ(x,y)=A
∑ |
|
|
|
∑ |
|
|
∑ ∑
4
∑
∑
где
Поскольку оптимальные оценки координат ИРИ соответствуют условию
P( ̂, ̂| |
λ( ̂, ̂ |
продифференцируем (5) по координате x, а потом по координате y и приравняем к нулю.
| ̂=
| ̂= |
(6) |
В результате решения уравнений (7а) получаем оптимальные оценки координат ИРИ:
̂= , ̂= , где AC- . (7)
Оценку точности измерения координат ( ̂, ̂) проведем из условия того (см.(5) и (6)), что коэффициенты A,B,C являются
элементами матрицы |
, |
обратной |
матрице |
Фишера K |
|||||||
[2.c.89], то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) ; |
( |
|
), |
(8) |
||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
. |
|
Учитывая, что элементы матрицы К являются элементами |
||
корреляционной матрицы |
[3] ошибок измерений |
|
( |
) |
(9) |
и сравнивая (8) и (9), окончательно можем записать:
|
|
= |
|
̂̂ |
|
, |
(10) |
|
|
|
|
||||
где |
|
|
|
̂, ̂ |
cоответствен- |
||
но, ̂ ̂ |
|
|
|
|
|
||
Справедливость преобразований (8) - (10) подтверждается тем, что
где I-единичная матрица.
Среднеквадратическое отклонение (СКО) оценок ̂, ̂ от истинного местоположения ИРИ определяется как
̂ |
̂ |
. |
(11) |
|
|
||
Поскольку в системах пассивной радиолокации, к кото- |
|||
рым относится УС, расстояние |
|
являются неизвестными, |
|
оценку координат ̂, ̂ИРИ необходимо выполнять методом последовательных приближений(методом итерации) [4] последующему алгоритму [5].
6

1. В начальной (первой) точке итерационного процесса
определяются пеленги |
|
по формуле |
||||||||||
|
|
|
|
|
|
|
|
|
, |
|
(12) |
|
|
|
|
|
|
|
|
|
|
||||
( |
|
|
|
) |
|
( |
|
|
|
) |
||
|
|
|
|
|
|
|||||||
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Определяются координаты x,y по выведенным на практических занятиях формулам
(13)
где |
. |
3. Определяются расстояния от ПП до ИРИ
7
4. Рассчитывается СКО измерения пеленгов
|
|
|
|
|
|
(14) |
|
|
|
|
|
|
|
||
|
|
√ |
|
||||
|
|
|
|
|
|||
где |
– ширина диаграммы направленности m-го пеленгатора |
||||||
по уровню половинной мощности; |
– отношение сигнал / |
||||||
|
|
|
|||||
шум по мощности на входе m-го пеленгатора; |
. |
||||||
5.Определяются коэффициенты квадратичной формы (A, B, C, D, E, F) по формулам (6).
6.Осуществляется оптимальная оценка координат ИРИ по формулам (7).
7.Оценка точности измеренных координат ̂ ̂ проводится по формулам (10), (11).
8.Осуществляется проверка выполнения условия
̂ |
̂ |
̂ |
̂ |
, |
(15) |
при выполнении которого расчеты останавливаются и на печать выводятся следующие результаты:
̂ ̂
При невыполнении указанного условия необходимо переходить к следующей (n+1)-ой точке итерационного процесса и осуществлять расчеты по изложенному выше алгоритму. При этом в расчетах по первым трем пунктам алгоритма вместо первоначально заданных координат (x,y) подставляются их оценки ̂ ̂ .
Для проведения расчетов по изложенной методике, которые могут проводиться методом имитационного моделирования на ЭВМ, необходимо задание следующих исходных данных:
8
