Учебное пособие 1053

которые вычеркнуты одной линией, через сij+ - те элементы, которые вычеркнуты одновременно горизонтальной и вертикальной линиями, невычеркнутые элементы сij помечать не будем.

Алгоритм выполнения третьего этапа Шаг 1. Найдем с = min сij (из невычеркнутых сij ).

Шаг 2. Элементы матрицы С преобразуются по следующему правилу: сij = сij −c (для невычеркнутых),

сij− = сij− (для вычеркнутых одной линией),

сij+ = сij+ + c (для вычеркнутых одновременно двумя линиями).

Шаг 3. S = S + (n − k)c .

Шаг 4. Переход ко второму этапу.

Покажем, что приведенный алгоритм есть формализация преобразования матрицы с помощью (n + k ) шагов, основанных на первом свойстве матрицы С. Шаги 2-3 могут быть представлены следующим образом.

Шаг 2. Из всех строк вычисляется с, то есть cij = cij −c .

Шаг 3. S = S + nc .

Шаг 4. Ко всем вычеркнутым строкам и столбцам прибавляется число с, то есть все вычеркнутые сij определяются по формуле cij = cij + c .

Шаг 5. S = S + nc − kc = S + c(n − k).

Отсюда получается, что после второго шага все элементы матрицы С уменьшаются на величину c. Следовательно, все нули становятся отрицательными числами, равными (−c ), после четвертого шага все вычеркнутые элементы увеличиваются на с, при этом если элементы были вычеркнуты одной линией, то они не изменяются по сравнению с исходными значениями, а те элементы, которые были вычеркнуты горизонтальной и вертикальной линиями, одновременно увеличились на с, так как с один раз вычиталось и два раза прибавлялось. Именно эта процедура описана в алгоритме, но более кратко.

Этап 4. Поиск независимых нулей и получение оптимального решения

Алгоритм четвертого этапа подобен алгоритму второго этапа, однако имеет некоторые модификации.

Алгоритм выполнения четвертого этапа.

Шаг 1. В матрице размера (n ×n ) помечаются места всех нулей.

Шаг 2. L = n .

Шаг 3. Отыскивается строка, содержащая один ноль. Этот ноль выделяется, а соответствующие строка и столбец вычеркиваются. L = n −1. (Процесс продолжается пока существует строка, содержащая один ноль.)

Шаг 4. Если L = 0, то переход к Шагу 11. Иначе Шаг 5.

51

Шаг 5. Отыскивается столбец, содержащий один ноль. Этот ноль выделяется, а соответствующие строка и столбец вычеркиваются. L = n −1. (Процесс продолжается пока существует столбец, содержащий один ноль.)

Шаг 6. Если L = 0, то переход к Шагу 11. Иначе Шаг 7.

Шаг 7. Просматриваются строки и определяется k1 = min ki – число невычеркнутых нулей в i-й строке.

Шаг 8. Просматриваются строки и определяется k2 = min k j – число не-

вычеркнутых нулей в j-м столбце.

Шаг 9. Если k1 ≤ k2 , то выбирается строка, содержащая k1 нулей, один из

нулей выделяется, а строка и столбец вычеркиваются. L = L −1. Переход к Шагу 3.

Шаг 10. Если k1 > k2 , то выбирается столбец, содержащий k2 нулей, один

из нулей выделяется, а строка и столбец вычеркиваются. L = L −1. Переход к Шагу 3.

Шаг 11. На исходной матрице С помечаются элементы cij соответствую-

щие помеченным нулям.

Шаг 12. Вычисляется целевая функция c(x) = ∑cij .

Шаг 13. Сравнивается c(x) и S. Эти значения должны совпасть. Пример 5.1 Дана матрица С (рис. 5.5). Решить задачу о назначениях.

Рис. 5.5

Этап 1

Шаг 0. S=0. Шаг 1 (рис. 5.6).

52

Шаг 2. Из строк матрицы вычитаем соответствующее ai (рис. 5.7)

Рис. 5.8

Шаг 5. Из каждого столбца вычитаем соответствующее bj (рис. 5.9).

Шаг 6. S=20+0+1+1+3+4+5=34.

Этап 2

Подсчет k – числа независимых нулей (рис. 5.10)

k = 4 переход к Этапу 3.

53

Этап 3

Шаг 1. с=1.

Шаг 2. Элементы матрицы С (рис. 5.110преобразуются по следующему правилу:

сij = сij −c (для невычеркнутых),

сij− = сij− (для вычеркнутых одной линией),

сij+ = сij+ + c (для вычеркнутых одновременно двумя линиями).

Шаг 3. S = 34 + (6 − 2) 1 = 36.

Переход к этапу 2.

Этап 2

Подсчет k – числа независимых нулей (рис. 5.112).

k1 = 3, k2 = 2 : k1 < k2 . Выбираем столбец. k = 5. Переход к этапу 3.

Шаг 1. с=1.

Шаг 2. Аналогично предыдущей итерации (рис. 5.13).

Шаг 3. S = 34 + (6 −5) 1 = 37 .

54

Переход к этапу 2 (рис. 5.14).

Рис. 5.15

Переносим места выделенных нулей на исходную матрицу С. Получаем

C(x) = 4 + 4 + 4 +11+ 4 +10 = 37 = S .

Лабораторная работа №7

Дана матрица С (рис. 5.16).

Рис. 5.16

Решить задачу о назначениях.

Для каждого варианта в исходной матрице С вычеркнуть три элемента. Координаты вычеркиваемых элементов приведены в табл. 5.1.

55

5.4. Система конвейерного типа с двумя приборами

5.4.1 Постановка задачи

Вербальная модель

Имеем n деталей, которые должны быть обработаны последовательно на первом и втором станках.

аi – время обработки на первом станке, bj – время обработки на втором станке.

Требуется определить, в какой последовательности следует обрабатывать детали, чтобы выполнить эту работу за минимальное время.

Задача Джонсона

В сборном концерте должны выступать n артистов. Каждый из них должен готовиться к своему номеру в течение времени аi , а время пребывания ар-

тиста на сцене – bj . В гримерной одновременно может находиться один чело-

век, так же как и на сцене. Требуется определить порядок выхода артистов на сцену, так чтобы время перерывов было минимально.

Вербальная модель Задачи Джонсона в терминах теории расписаний

Имеем n требований, каждое их которых должно быть последовательно обслужено на первом и втором приборах.

аi – время обслуживания i-го требования на 1-м приборе; bj – время обслуживания i-го требования на 2-м приборе.

Требуется задать расписание обслуживания, минимизирующее общее время обслуживания.

56

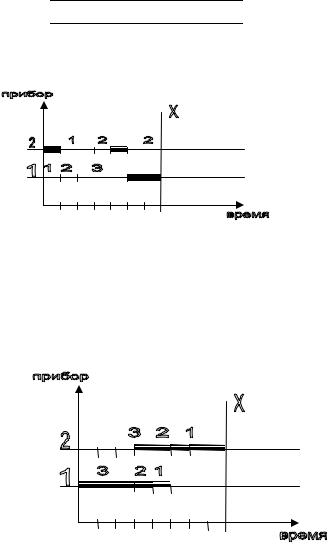
5.4.2. Диаграмма Гантта

Любое расписание для конвейерной системы можно представить в виде

диаграммы Гантта.

Рассмотрим систему из трех требований, исходные данные для которой представлены в табл. 5.2.

Таблица 5.2

(рис. 5.17):

1 2 3 4 5 6 7

Рис. 5.17

На рис. 5.17 жирной линией показано время простоя, а Х – общее время обслуживания и Х=7.

Если требования обслуживать в порядке σ2 = (3,2,1), то диаграмма Гантта будет иметь следующий вид (рис. 5.18):

1 2 3 4 5 6

Рис. 5.18

Общее время обслуживания Х=8.

Рис. 5.17-5.18 показывает, что длина расписания зависит от порядка обслуживания требований.

5.4.3. Вычисление длины расписания

Пусть задано расписание σ , введем обозначения:

fi a (σ) – момент завершения обслуживания на первом приборе требования, стоящего в расписании σ на i-м месте;

57

fib (σ) – момент завершения обслуживания на втором приборе требования, стоящего в расписании σ на i-м месте;

F max (σ) – длина расписания σ .

Так как требования обслуживаются последовательно, то длина расписания – это момент завершения обслуживания последнего требования на втором приборе, то есть

F max (σ) = fnb (σ).

Из анализа диаграмм Гантта (см. рис. 5.4.1-5.4.2) получаем формулы для вычисления fi a (σ) , fib (σ):

f1a (σ) = ai ,

fi a (σ) = fi−a1(σ) +ai ,

f1b (σ) = f1a +b1 ,

fi a (σ) = max( fi a (σ); fi−a1(σ)) +bi , fib (σ) = max( fi a (σ); fi−b1(σ)) +bi .

Пример 5.2. Дано пять деталей, которые последовательно обрабатываются на двух станках. Время обработки каждой детали на каждом станке указано в табл. 5.3.

Таблица 5.3

Если составить расписание обработки деталей в данном порядке, то получим

(табл. 5.4)

Таблица 5.4

Здесь общее время обработки деталей составило 18. Возьмем другое расписание: σ = (2,4,1,5,3), (табл. 5.5).

Таблица 5.5

Здесь общее время обслуживания равно 16.

58

Достаточное условие оптимальности расписания

Теорема. Если в расписании σ для любого требования i предшествующего j выполняется условие

то расписание оптимально.

5.4.4. Алгоритм построения расписания минимальной длины

Условие (5.4.1) является достаточным для оптимальности расписания. То есть если для любой пары требований (i, j) из некоторого расписания условие (5.4.1) выполнено, то расписание оптимально. Однако строить оптимальное расписание с его помощью не слишком удобно, так как требуется большое количества проверок и переборов. Поэтому ниже будет предложен алгоритм построения расписания, удовлетворяющего условию (5.4.1), то есть являющегося оптимальным.

Алгоритм Джонсона

Шаг 1. В первую группу заносятся требования, у которых ai ≤ bi ; во вторую группу заносятся требования, у которых ai > bi .

Шаг 2. Требования из первой группы сортируются по неубыванию аi и в таком порядке занимают первые место в расписании.

Шаг 3. Требования из второй группы сортируются по невозрастанию bi и занимают в таком порядке последующие места в расписании.

Пример 5.3. Дано пять деталей, которые последовательно обрабатываются на двух станках. Время обработки каждой детали на каждом станке указано в табл. 5.4.5.

Таблица 5.6

В соответствии с требованиями алгоритма разобьем требования на группы

(табл. 5.7):

Таблица 5.7

Оптимальное расписание σ = (2,4,5,3,1).

Длина расписания вычисляется в табл. 5.8.

59

Таблица 5.8

Здесь общее время обслуживания равно 16.

Замечание о сложности алгоритма. Поскольку алгоритм построения оптимального расписания состоит из сортировки, а сложность сортировки имеет порядок N ln N , то можно сказать, что задача Джонсона с двумя приборами имеет полимиальную сложность.

5.5. Конвейерная система с тремя и более приборами

Как было показано выше, задача построения оптимального расписания с двумя приборами имеет полимиальную сложность.

К сожалению, если система имеет три и более прибора, то в общем случае она является NP-трудной задачей, то есть не существует простых алгоритмов построения оптимального расписания для такой системы.

Однако существуют частные случаи, в которых возможно построение оптимального расписания с помощью простых алгоритмов.

Будем рассматривать в дальнейшем систему с тремя приборами. Длительность обслуживания требований на первом, втором и третьем приборах обозначим ai , bi и сi соответственно.

5.5.1. Вычисление длины расписания для системы с тремя приборами

Пусть время обслуживания требований на первом, втором и третьем приборах ai , bi , сi и fi a , fib , fic – моменты завершения обслуживания требова-

ния, стоящего на i-м месте в расписании на первом, втором и третьем приборах соответственно.

Тогда

f1a (σ) = ai ,

Пример 5.4. Дано пять деталей, которые последовательно обрабатываются на трех станках. Время обработки каждой детали на каждом станке указано в табл. 5.9. Вычислить длину расписания.

60