
Учебное пособие 938
.pdf
при тесной линейной корреляционной зависимости, а точки корреляционного поля будут примыкать к этим прямым.
ПРИМЕР ТИПОВОГО ВАРИАНТА
ЗАДАЧА 1. Результаты 100 измерений случайной величины X представлены в виде вариационного ряда в таблице.
2,0 |
4,9 |
6,4 |
7,1 |
8,1 |
8,6 |
9,1 |
9,8 |
|
10,7 |
12,3 |
3,0 |
5,0 |
6,5 |
7,2 |
8,1 |
8,7 |
9,1 |
9,8 |
|
10,8 |
12,5 |
4,0 |
5,1 |
6,6 |
7,3 |
8,2 |
8,7 |
9,2 |
9,9 |
|
10,9 |
12,8 |
4,1 |
5,3 |
6,6 |
7,5 |
8,2 |
8,8 |
9,3 |
10,0 |
|
11,1 |
13,1 |
4,3 |
5,6 |
6,7 |
7,7 |
8,3 |
8,8 |
9,4 |
10,0 |
|
11,2 |
13,5 |
|
||||||||||
4,4 |
5,9 |
6,8 |
7,8 |
8,3 |
8,9 |
9,4 |
10,1 |
|
11,4 |
13,9 |
4,5 |
6,0 |
6,9 |
7,8 |
8,4 |
8,9 |
9,5 |
|
|
11,6 |
|
10,2 |
|
14,4 |
||||||||
4,6 |
6,1 |
7,0 |
7,9 |
8,4 |
9,0 |
9,5 |
10,3 |
|
11,8 |
14,9 |
4,8 |
6,2 |
7,0 |
8,0 |
8,5 |
9,0 |
9,6 |
10,5 |
|
11,9 |
15,4 |
4,8 |
6,3 |
7,1 |
8,0 |
8,6 |
9,0 |
9,7 |
10,6 |
|
12,1 |
16,0 |
Требуется:
1.Представить опытные данные в сгруппированном виде, разбив на k равноотстоящих частичных интервалов.
2.Найти эмпирическую функцию распределения и построить ее график.
3.Построить полигон и гистограмму относительных частот.
4.Вычислить методом условных вариант числовые характеристики выборки: выборочную среднюю, выборочную и исправленную дисперсии, выборочное среднее квадратическое отклонение и выборочное исправленное среднее квадратическое отклонение.
5.Проверить, согласуется ли принимаемая гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий χ2 Пирсона при уровне значимости 0,05.
6.Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0,95 .
ЗАДАЧА 2. Найти выборочный коэффициент корреляции по экспериментальным данным из приведенной таблицы, выборочные уравнения линейной регрессии Y на X и X на Y . Изобразить корреляционное поле и графики прямых линий регрессии.
nij |
|
|
|
X |
|
|
|
||
8 |
14 |
20 |
|
26 |
32 |
38 |
|
||
|
|
|
|
||||||
|
6 |
4 |
2 |
|
|
|
|
|
|
Y |
12 |
|
6 |
2 |
|
|
|
|
|
18 |
|
1 |
5 |
|
40 |
3 |
|
|
|
|
24 |
|
|
|
|
8 |
7 |
|
|
|
30 |
|
|
|
|
|
7 |
8 |
|
11
РЕШЕНИЕ ТИПОВОГО ВАРИАНТА
ЗАДАЧА 1.
1. Для построения интервального распределения частот, найдем число интервалов k , используя формулу Стерджеса, где объем выборки n =100 :
k ≈1 +3,322 lg100 =1 +3,322 2 = 7,644 ≈8 .
Затем вычислим длину частичного интервала, округлив полученное значение:
|
|
|
h ≈ |
16 −2 |
=1,75 ≈1,8 . |
|
|
|
||||
|
|
|
|
8 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Тогда интервальное распределение частот будет иметь вид: |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
xj − xj+1 |
2 - 3,8 |
3,8 - 5,6 |
5,6 - 7,4 |
|
7,4 - 9,2 |
9,2 - 11 |
|
11 - 12,8 |
12,8-14,6 |
14,6-16,4 |
||
ni |
2 |
12 |
19 |
|
29 |
|
21 |
|
9 |
5 |
3 |
|
Вычисляя относительные частоты по формуле wi = ni / n (i =1,..., k ), полу- |
||||||||||||
чим интервальное распределение относительных частот: |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
xj − xj+1 |
2 - 3,8 |
3,8 - 5,6 |
5,6 - 7,4 |
|
7,4 - 9,2 |
9,2 - 11 |
11 - 12,8 |
12,8-14,6 |
14,6-16,4 |
|||
wi |
0,02 |
0,12 |
0,19 |
|
0,29 |
|
0,21 |
|
0,09 |
0,05 |
0,03 |
|
2. Для того, чтобы найти эмпирическую функцию распределения перейдем от интервального распределения частот к статистическому распределению частот, взяв в качестве xi середины интервалов:
xi |
2,9 |
4,7 |
6,5 |
8,3 |
10,1 |
11,9 |
13,7 |
15,5 |
ni |
2 |
12 |
19 |
29 |
21 |
9 |
5 |
3 |
Тогда статистическое распределение относительных частот запишем в виде:
xi |
2,9 |
4,7 |
6,5 |
8,3 |
10,1 |
11,9 |
13,7 |
15,5 |
wi |
0,02 |
0,12 |
0,19 |
0,29 |
0,21 |
0,09 |
0,05 |
0,03 |
Теперь, согласно определению эмпирической функции распределения, имеем: 12

|
0, |
|
0,02, |
|
|
|
0,14, |
|
|
|
0,33, |
|
0,62, |
F * (x) = |
|
|
0,83, |
|
|
0,92, |
|
|
|
0,97, |
|
|
1, |
|
|
x ≤ 2,9; 2,9 < x ≤ 4,7; 4,7 < x ≤ 6,5; 6,5 < x ≤8,3; 8,3 < x ≤10,1; 10,1 < x ≤11,9; 11,9 < x ≤13,7; 13,7 < x ≤15,5;
x >15,5.
График эмпирической функции распределения показан на рис. 1.
Рис. 1. График эмпирической функции распределения
3. Для построения полигона относительных частот воспользуемся статистическим распределением относительных частот. Соединив соседние точки (xi , wi ) отрезками прямых линий, мы получим полигон относительных частот
(рис. 2).
Для построения гистограммы воспользуемся интервальным распределением относительных частот. На оси абсцисс откладываем частичные интервалы, а на каждом из них строим прямоугольник высотой wi 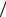 h .
h .
13

Рис. 2. Полигон относительных частот
Рис. 3. Гистограмма относительных частот
14

Гистограмму и полигон относительных частот удобно использовать для визуального подбора модели распределения случайной величины X . В частности, в нашем случае естественно выдвинуть гипотезу, что у нас нормальный закон распределения.
4. Вычислять числовые характеристики выборки будем, используя метод условных вариант, который значительно упрощает вычисления и заключается в переходе к условным вариантам:
ui |
= |
xi − M |
, |
|
h |
||||
|
|
|
||
где M - мода вариационного ряда. |
|
|
|
Составим вспомогательную таблицу:
xi |
ni |
ui = |
xi −8,3 |
|
ni ui |
u 2 |
n u |
2 |
|
|
|||||||
|
|
1,8 |
|
|
i |
i i |
||
|
|
|
|
|
|
|
||
2,9 |
2 |
-3 |
|
-6 |
9 |
18 |
|
|
4,7 |
12 |
-2 |
|
-24 |
4 |
48 |
|
|
6,5 |
19 |
-1 |
|
-19 |
1 |
19 |
|
|
8,3 |
29 |
0 |
|
0 |
0 |
0 |
|
|
10,1 |
21 |
1 |
|
21 |
1 |
21 |
|
|
11,9 |
9 |
2 |
|
18 |
4 |
36 |
|
|
13,7 |
5 |
3 |
|
15 |
9 |
45 |
|
|
15,5 |
3 |
4 |
|
12 |
16 |
48 |
|
|
∑ |
100 |
|
|
|
17 |
|
235 |
|
Найдем числовые характеристики для случайной величины U . Выборочная средняя:
|
|
u |
= |
1 |
∑k |
niui |
= |
|
17 |
= 0,17 |
|
||||
|
|
|
100 |
|
|||||||||||
|
|
|
|
|
n i=1 |
|
|
|
|
|
|
|
|||
Выборочная дисперсия: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Dв(U ) = |
1 ∑k |
niui |
2 −( |
u |
)2 = 235 |
−(0,17)2 |
≈ 2,32 |
||||||||
|
n i=1 |
|
|
|
|
|
|
|
100 |
|
|
||||
Тогда числовые характеристики для искомой случайной величины рассчитываются по формулам:
Выборочная средняя:
x = M + h x =8,3 +1,8 0,17 ≈8,606 .
Выборочная дисперсия:
15

Dв( X ) = h2 Dв(U ) =1,82 2,32 ≈7,52 .
Выборочное среднее квадратическое отклонение:
σв( X ) = 7,52 ≈ 2,74
Выборочное исправленное среднее квадратическое отклонение:
S = |
100 |
7,52 ≈ 2,75. |
|
99 |
|
5. Для проверки согласуется ли принимаемая гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, будем использовать критерий χ2 -Пирсона, который заключается в сравне-
нии эмпирических и теоретических частот. Эмпирические частоты нам известны из опыта, а теоретические требуется найти.
Вычислим теоретические вероятности pi попадания случайной величины X , распределенной по нормальному закону с параметрами a =8,606 и σ = 2,74 в частичные интервалы по формуле:
|
|
|
|
|
|
pi = P(xi ≤ X < xi+1 )= Φ(zi+1 ) −Φ(zi ) , i =1,..., m , |
|||||||
где zi |
= |
xi − x |
, zi+1 |
= |
xi+1 − x |
, Φ(z) - функция Лапласа, значения которой можно |
|||||||
|
|
|
|||||||||||
|
|
|
σ |
|
|
|
|
σ |
|
|
|
|
|
найти по таблице [5, с.80], m - число частичных интервалов. |
|
|
|||||||||||
|
|
Искомые теоретические частоты находят по формуле: ni ' = n pi . |
|||||||||||
|
|
Вычисления, необходимые для отыскания теоретических частот, приве- |
|||||||||||
дем в таблице: |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(xi ; xi+1 ) |
|
|
|
(zi ; zi+1 ) |
pi |
|
ni ' = n pi |
|||
|
|
(2 ;5,6) |
|
|
( −∞;-1,09) |
0,1379 |
|
13,79 |
|
||||
|
|
(5,6 |
;7,4) |
|
|
(-1,09;-0,44) |
0,1921 |
|
19,21 |
|
|||
|
|
(7,4 |
;9,2) |
|
|
(-0,44;0,21) |
0,2532 |
|
25,32 |
|
|||
|
|
(9,2 ;11) |
|
|
(0,21;0,87) |
0,2246 |
|
22,46 |
|
||||
|
|
(11 ;12,8) |
|
|
(0,87;1,53) |
0,1282 |
|
12,82 |
|
||||
|
|
(12,8 |
;16,4) |
|
|
(1,53; +∞) |
0,063 |
|
6,3 |
|
|||
Отметим, что первый и второй, а также два последних интервала были объединены, так как малочисленные группы ( ni <8) следует объединять, сумми-
руя частоты. Кроме того, так как нормально распределенная случайная величина определена на (−∞;+∞) , то наименьшее значение первого интервала заменя-
ется на −∞, а наибольшее значение последнего интервала на +∞.
16

В качестве критерия проверки нулевой гипотезы примем случайную величину:
χ2 = ∑ |
(ni −ni ')2 . |
i |
ni ' |
Можно показать, что если нулевая гипотеза верна, что при n → +∞ закон |
|
распределения случайной величины |
χ2 независимо от того, какому закону |
распределения подчинена генеральная совокупность, стремится к закону распределения χ2 с k степенями свободы. Число степеней свободы находят по формуле: k = m −1 −r , где r - число параметров предполагаемого распределения.
Для того, чтобы при заданном уровне значимости (α = 0,05 ) проверить нулевую гипотезу H0 : генеральная совокупность распределена по нормальному закону, надо сначала вычислить наблюдаемое значение критерия
|
|
χнабл2 = ∑(ni |
−ni ')2 |
|
|
|
|
||
|
|
|
i |
ni ' |
|
|
|
|
|
Необходимые вычисления приведем в таблице: |
|||||||||
|
|
|
|
|
|
(ni −ni ')2 |
|
|
|
|
ni |
|
ni ' = n pi |
|
|
||||
|
|
|
ni ' |
|
|
||||
|
|
|
|
|
|
|
|
||
|
14 |
|
13,79 |
|
|
0,003 |
|
|
|
|
19 |
|
19,21 |
|
|
0,002 |
|
|
|
|
29 |
|
25,32 |
|
|
0,534 |
|
|
|
|
21 |
|
22,46 |
|
|
0,094 |
|
|
|
|
9 |
|
12,82 |
|
|
1,138 |
|
|
|
|
8 |
|
6,3 |
|
|
0,458 |
|
|
|
В результате получим |
χнабл2 = 2,229 . По таблице критических точек рас- |
||||||||
пределения χ2 [2, с. 465] и уровню значимости α = 0,05 и числу степеней свободы k =6 −1 − 2 ( r = 2 , так как нормальный закон распределения имеет два параметра a и σ ) находим χкр2 =7,8 . Так как χнабл2 < χкр2 - нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
6. Найдем интервальные оценки параметров нормального распределения. Для вычисления доверительного интервала воспользуемся таблицей значений t(γ, n) и q(γ, n) , так как по условию доверительная вероятность равна γ = 0,95 ,
а объем выборки n =100 , получаем:
17

t(0,95;100) =1,984 ; q(0,95;100) = 0,143;
Искомый доверительный интервал для математического ожидания
8,606 −1,984 2,75100 < a <8,606 +1,984 2,75100 ,
8,06 < a <9,15
Искомый доверительный интервал для среднего квадратического откло-
нения
2,75(1 −0,143) <σ < 2,75(1 +0,143) ,
2,36 <σ < 3,14 .
ЗАДАЧА 2.
Найдем значения числовых характеристик необходимых для отыскания выборочного коэффициента корреляции и выборочных уравнений линейной регрессии Y на X и X на Y .
Все вычисления будем сводить в таблицы. Начнем с отыскания числовых характеристик случайной величины X .
xi |
ni |
ni xi |
x 2 |
n x 2 |
|
|
|
i |
i i |
8 |
4 |
32 |
64 |
256 |
14 |
9 |
126 |
196 |
1764 |
20 |
7 |
140 |
400 |
2800 |
26 |
48 |
1248 |
676 |
32448 |
32 |
17 |
544 |
1024 |
17408 |
38 |
8 |
304 |
1444 |
11552 |
∑ |
93 |
2394 |
|
66228 |
Найдем числовые характеристики для случайной величины X . Выборочная средняя:
|
x = 2394 |
≈ 25,74 . |
|
93 |
|
Выборочная дисперсия: |
|
|
D |
( X ) = 66228 − |
(25,74)2 ≈ 49,58 . |
в |
93 |
|
|
|
|
Выборочное среднее квадратическое отклонение:
18

σв( X ) = 49,58 ≈7,04 .
Аналогично, можно найти числовые характеристики случайной величины
Y : y ≈19,61; Dв(Y ) ≈38,93; σв(Y ) ≈6,24 .
Далее найдем выборочную среднюю произведенияXY по формуле:
|
= |
1 |
∑∑nij xi y j |
= |
4 8 6 + 2 14 6 + 6 14 12 +... +8 38 30 |
= |
50412 |
≈542,06. |
|
xy |
|||||||||
n |
93 |
93 |
|||||||
|
|
i j |
|
|
|
Тогда выборочный коэффициент корреляции равен:
ρв( X ,Y ) = |
542,06 −25,74 19,61 |
≈ 0,849 . |
|
7,04 6, 24 |
|
Так как значение выборочного коэффициента корреляции близко к единице, то можно говорить о достаточно тесной линейной корреляционной зависимости между случайными величинами X и Y .
Подставим найденные значения числовых характеристик в следующие формулы:
|
y |
|
− y = ρ |
|
σв (Y ) |
(x − x ), |
x |
|
− x = ρ |
σв (X ) |
(y − y ). |
|||||
|
|
|
|
|
|
|
|
|||||||||
|
x |
в σ |
в (X ) |
y |
в σв (Y ) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
Тогда |
|
|
|
|
|
|
6,24 |
|
|
|
|
|
|||
|
|
|
|
yx |
−19,61 =0,849 |
(x − 25,74), |
|
|||||||||
|
|
|
|
7,04 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
yx |
=0,75x + 0,24 - выборочное уравнение прямой линии регрессии Y на X . |
|||||||||||||||
|
Аналогично, |
|
|
|
|
|
|
|
7,04 |
|
|
|
|
|||
|
|
|
|
|
|
xy − 25,74 =0,849 |
(y −19,61), |
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
6,24 |
|
|
|
|
||
xy |
=0,96 y + 6,95 - выборочное уравнение прямой линии регрессии X на Y . |
|||||||||||||||
Корреляционное поле и прямые регрессии изображены на рис. 4.
19
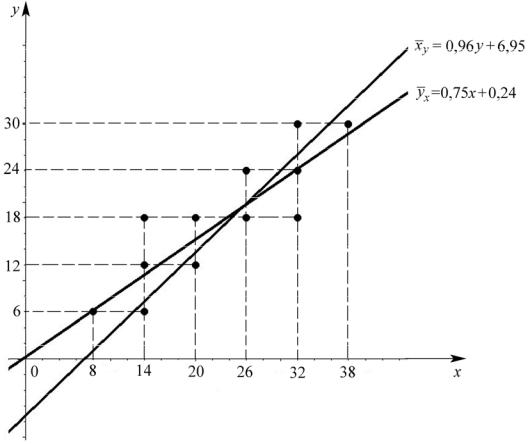
Рис. 4. Корреляционное поле и прямые регрессии
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
ЗАДАЧА 1
Результаты измерений случайной величины X представлены в виде вариационного ряда в таблице.
Для каждого варианта требуется:
1.Представить опытные данные в сгруппированном виде, разбив на k равноотстоящих частичных интервалов.
2.Найти эмпирическую функцию распределения и построить ее график.
3.Построить полигон и гистограмму относительных частот.
4.Вычислить методом условных вариант числовые характеристики выборки: выборочную среднюю, выборочную и исправленную дисперсии, выборочное среднее квадратическое отклонение и выборочное исправленное среднее квадратическое отклонение.
5.Проверить, согласуется ли принимаемая гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий χ2 Пирсона при уровне значимости 0,05.
6.Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность γ = 0,95 и γ = 0,99 .
20
