
Методические указания к курсовому проектированию по дисциплине «Технология и методы программирования». Карпеев Д.О
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра систем информационной безопасности
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к курсовому проектированию по дисциплине «Технология и методы программирования» для студентов специальности
090303 «Информационная безопасность автоматизированных систем»
очной формы обучения
Воронеж 2014
Составитель канд. техн. наук Д. О. Карпеев
УДК 004.056.5: 004.42
Методические указания к курсовому проектированию по дисциплине «Технология и методы программирования» для студентов специальности 090303 «Информационная безопасность автоматизированных систем» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. Д. О. Карпеев. Воронеж,
2014. 21 с.
Методические указания содержат материал, регламентирующий процесс работы над курсовым проектом, включая практические навыки по созданию и программной реализации алгоритмов, применению технологий программирования, процесс закрепления знаний, полученных в лекционном курсе.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2013 и содержатся в файле Карпеев_КП_Технология и методы программирования.pdf
Табл. 1. Ил. 1. Библиогр.: 4.
Рецензенты: ОАО «Концерн «Созвездие» (канд. техн. наук, ст. науч. сотрудник О.В. Поздышева);
д-р техн. наук, проф. А.Г. Остапенко
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А.Г. Остапенко
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский государственный технический университет», 2014
1.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1.Понятие сложности алгоритма
Время рассчитывается в относительных единицах так, чтобы эта оценка, по возможности, была одинаковой для машин с разной тактовой частотой и с незначительными вариациями в архитектуре [1].
Такой подход сложился исторически и ориентируется прежде всего на научные и инженерные приложения теории алгоритмов: объемы данных значительно превышают размеры самой программы, а программа может выполняться несколько часов. Если не считать офисных и бухгалтерских применений вычислительных машин, то производительность и объем памяти компьютера никогда не казались программистам чрезмерными и постоянной задачей является сделать программу работающей хотя бы немного быстрее и попытаться заставить ее работать в стесненных условиях ограниченного поля памяти.
В данном разделе будут рассмотрены две характеристики сложности алгоритмов – временная и емкостная. Не будем обсуждать сложность (длину) текста алгоритма, поскольку она больше характеризует исполнителя (машину), его язык, а не метод решения задачи. Не будем также обсуждать логическую сложность разработки алгоритма – сколько человеко-месяцев нужно потратить на создание программы, поскольку не представляется возможным дать объективные количественные характеристики. Обе эти темы относятся к области компьютерных наук, называемой «технология программирования»
(software engineering).
Единицы измерения сложности будем привязывать к классу архитектур, наиболее распространенных ЭВМ. Временную сложность будем подсчитывать в исполняемых командах: количество арифметических операций, количество сравнений, пересылок (в зависимости от алгоритма). Емкостная сложность будет определяться количеством скалярных переменных, элементов массивов, элементов записей или просто количеством байт.
Одно из свойств алгоритма – массовость. Поэтому сложность алгоритма a рассматривается как функция от некоторого интегрированного числового параметра V, характеризующего исходные данные. Обозначим: Ta(V) – временная сложность алгоритма a; Sa(V) – емкостная сложность [4].
Параметр V, характеризующий данные, называют иногда объемом данных или сложностью данных. Оба эти термина не совсем точны. Выбор параметра V зависит не только от вида данных, но и от вида алгоритма или от задачи, которую этот алгоритм решает.
Рассмотрим два примера.
Задача 1: вычисления факториала числа x (x>0). Программа итеративного решения задачи имеет следующий вид:
function Factorial (х: integer): integer; var
m, i: integer; begin
m := 1;
for i := 2 to x do m := m*i;
Factorial := m; end;
Количество операций здесь подсчитывается легко: один раз выполняется оператор m := 1; тело цикла (умножение и присваивание) выполняется (х-1) раз; один раз выполняется присваивание Factorial := m. Если сложность каждой из элементарных операций считать равной единице, то временная сложность приведенного алгоритма будет равна 1+2(x-1)+1=2х. Из этого анализа ясно, что за параметр V удобно принять значение х.
Задача 2: отыскания скалярного произведения двух векторов A = (a1, a2, ... , ak), В = (b1, b2, ..., bk). Вектор вход-
ных данных X = (А, В), n = 2k. Стандартный алгоритм циклического сложения попарных произведений компонент векто-
2
ров выполняет пропорциональное k число операций, т.е. можно взять V = k = n/2. Зависимости сложности алгоритма от значений ai и bi нет, имеется лишь зависимость от количества компонент.
Эти два примера иллюстрируют ситуации, когда для оценки сложности важны значения исходных данных (1) и количество исходных данных (2). Первая ситуация является более общей, так как k во втором примере фактически тоже входит в перечень исходных данных. Однако второй пример показывает, что от некоторых исходных данных сложность алгоритма может не зависеть. Собственно говоря, для анализа сложности не всегда можно сформулировать интегральный параметр V и лишь после построения оценки становится ясно, какая характеристика исходных данных является значимой для данного алгоритма [3].
Отыскание функций сложности алгоритмов важно, как с прикладной, так и с теоретической точек зрения. В практике проектирования систем реального времени задача разработки программы формулируется так: отыскать такой алгоритм a, решающий задачу P, что Тa(X) < Tmax при X Î D, где D - область допустимых значений входных данных (задача с ограничением на временную сложность).
Для алгоритмов решения систем линейных уравнений методом Гаусса, перемножения матриц, вычисления значений многочленов просто отыскать параметр V сложности исходных данных – это размер матрицы или степень многочлена. Сложность алгоритма при этом однозначно зависит от V.
Двойственная задача минимизации емкостной сложности при ограничениях на временную сложность возникает реже в силу архитектурных особенностей современных ЭВМ. Дело в том, что запоминающие устройства разных уровней, входящие в состав машины, построены так, что программе может быть доступна очень большая, практически неограниченная область памяти - виртуальная память. Недостаточное количество основной памяти приводит лишь к некоторому замедлению работы из-за обменов с диском. Если учесть, что в
3
любой момент времени программа работает лишь с двумятремя значениями и использование кэша и аппаратного просмотра команд программы вперед позволяет заблаговременно перенести с диска в основную память нужные значения, то можно констатировать, что минимизация емкостной сложности не является первоочередной задачей. Поэтому в дальнейшем будем интересоваться в основном временной сложностью алгоритмов.
Выход состоит в следующем. Множество D комбинаций исходных данных все-таки разбивается «каким-либо разумным образом» на классы, и каждому классу приписывается некоторое значение переменной V. Например, если мы хотим оценить сложность алгоритма анализа арифметических выражений, то в один класс можно поместить все выражения, состоящие из одинакового числа символов (строки одинаковой длины) и переменную V сделать равной длине строки. Это разумное предположение, так как с увеличением длины сложность должна увеличиваться: припишем к выражению длины n строку +1 – получится выражение длины 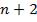 , требующее для
, требующее для
анализа больше операций, чем предыдущее. Но строгого (линейного) порядка нет. Среди выражений длины n может найтись более сложное (в смысле анализа), чем некоторое выражение длины n+2, не говоря уже о том, что среди выражений равной длины будут выражения разной сложности [2].
Затем для каждого класса (с данным значением V) оценивается количество необходимых операций в худшем случае, т.е. для набора исходных данных, требующих максимального количества операций обработки (сложность для худшего случая – верхняя оценка), и в лучшем случае – для набора, требующего минимального количества операций. Таким образом, получаются верхняя и нижняя оценки сложности алгоритма (см. рисунок ниже).
4
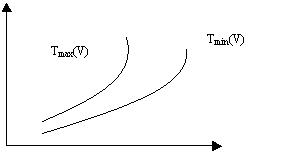
Зависимость сложности алгоритма от сложности данных
Разница между Tmax(V) и Tmin(V) может быть значительной. Но для многих алгоритмов отмечается ситуация «редкости крайних значений»: только на относительно небольшом количестве сочетаний исходных данных реализуются близкие к верхним или нижним оценкам значения сложности. Поэтому интересно бывает отыскать некоторое «усредненное» по всем данным число операций (средняя оценка). Для этого привлекаются комбинаторные методы или методы теории вероятностей. Полученное значение и считается значением Тa(V) средней оценки.
Функции сложности для худшего случая и для средних оценок имеют практическое значение. Системы реального времени, работающие в очень критических условиях, требуют, чтобы неравенство Тa(X) < Tmах не нарушалось никогда; в этом случае нам нужна оценка для худшего случая. В других системах достаточно, чтобы это неравенство выполнялось в большинстве случаев; тогда мы используем среднюю оценку. Опять же в связи со свойством массовости алгоритма исследователей чаще интересуют именно средние оценки, но получать их обычно труднее, чем верхние оценки.
5
1.2. Пространственная и временная сложность
Рассмотрим пример 1 такой оценки. Некоторое агентство недвижимости имеет базу данных из n записей, причём каждая запись содержит одно предложение (что имеется) и один запрос (что требуется) относительно объектов недвижимости. Требуется подобрать варианты обмена – найти все такие пары записей, в которых предложение первой записи совпадает с запросом второй записи и наоборот. Допустим, что сравнение одной пары записей занимает одну миллисекунду. Тогда при поиске решения самым простым способом («лобовой» алгоритм) – каждая запись сравнивается со всеми другими – потребуется n(n-1)/2 сравнений.
Если в базе данных n=100, то решение будет получено за 4,95 секунды. Но если n=100 000 (более реальный вариант), то время получения решения составит 4 999 950 секунд, 1389 часов, 58 суток, 2 месяца. Причём это оценка времени подбора прямых вариантов, а в реальной жизни число участников обмена чаще всего больше двух.
Этот пример показывает, что при выборе алгоритма для решения задачи необходимо оценить размер задачи (количество входных данных) и эффективность алгоритма, решающего эту задачу.
Эффективность алгоритма оценивается по двум параметрам: по времени работы и необходимому объёму памяти.
Сложность по памяти (пространственная / ёмкостная сложность) алгоритма – количество памяти, необходимое для выполнения этого алгоритма, в зависимости от размера входных данных.
Компьютеры обладают ограниченным объемом памяти. Если две программы реализуют идентичные функции, то та, которая использует меньший объем памяти, будет более эффективна[2].
Временная сложность алгоритма – зависимость числа операций, выполняемых алгоритмом, от размера входных данных.
6
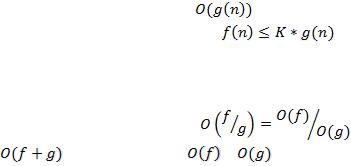
Замечание: время работы одного и того же алгоритма в секундах (минутах и т.д.) может отличаться для компьютеров с разным быстродействием, поэтому для универсальной оценки используют количество операций в алгоритме.
При подсчёте учитываются только существенные операции – операции сравнения двух значений, сложения, вычитания, умножения, деления, MOD, DIV, вычисление значений булевских операций OR, NOT, AND.
Операции вычисления SIN, COS, EXP, LOG и т.д. оцениваются через число сложений и умножений, т.к. их вычисление для конкретных значений реализуется разложением в ряд.
Операции присваивания и операции со счётчиком при организации цикла не учитываются, т.к. их выполнение занимает значительно меньше времени, а их доля в общем числе операций падает при существенном росте размера задачи.
Для конкретного алгоритма вычисление точного вида функции временной сложности довольно трудоёмко, поэтому на практике вместо точных формул используют сравнительные оценки поведения функции сложности с увеличением размера входных данных [4].
Математически асимптотическая сложность вычисляется с помощью О-функций (будем использовать «О-большое»). O-функции выражают относительную скорость алгоритма в зависимости от некоторой переменной (или переменных).
Функция f(n) имеет порядок |
) , если имеется |
константа К и счетчик n0, такие, что |
, для |
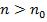 .
.
Основные соотношения для О-функций:
1)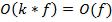 , где k – некоторая константа
, где k – некоторая константа
2) 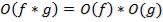 или
или
3) |
равна доминанте |
и |
7
1.3. Классы сложности
Для каждого класса существует категория задач, которые являются «самыми сложными». Это означает, что любая задача из класса сводится к такой задаче, и притом сама задача лежит в классе. Такие задачи называют полными задачами для данного класса. Наиболее известными являются NP-полные задачи.
В теории алгоритмов классами сложности называются множества вычислительных задач, примерно одинаковых по сложности вычисления. Говоря более узко, классы сложности
— это множества предикатов (функций, получающих на вход слово и возвращающих ответ 0 или 1), использующих для вычисления примерно одинаковые количества ресурсов[1].
Каждый класс сложности (в узком смысле) определяется как множество предикатов, обладающих некоторыми свойствами. Типичное определение класса сложности выглядит так: классом сложности X называется множество предикатов 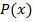 , вычислимых на машинах Тьюринга и использующих для
, вычислимых на машинах Тьюринга и использующих для
вычисления 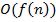 ресурса, где n — длина слова x[2].
ресурса, где n — длина слова x[2].
Все классы сложности находятся в иерархическом отношении: одни включают в себя другие. Однако про большинство включений неизвестно, являются ли они строгими. Одна из наиболее известных открытых проблем в этой области – равенство классов P и NP. Если это предположение верно (в чём большинство учёных сомневается), то представленная справа иерархия классов сильно свернётся. На данный момент наиболее распространённой является гипотеза о невырожденности иерархии (то есть все классы различны). Кроме того, известно, что EXPSPACE не равен классу PSPACE[3].
Рассмотрим функцию f и входную цепочку длиной n. Тогда класс DTIME(f(n)) определяют, как класс языков, принимаемых детерминированными машинами Тьюринга, заканчивающими свою работу за время, не превосходящее f(n). Класс NTIME(f(n)), в свою очередь, определяют, как класс
8
