Учебное пособие 773

ФГБОУ ВПО «Воронежский государственный технический университет»

Кафедра высшей математики и физико-математического моделирования

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРИ РЕШЕНИИ ПРИКЛАДНЫХ ЗАДАЧ

для организации самостоятельной работы по курсу «Математика» раздела «Теория вероятностей и мате-

матическая статистика» для студентов специальности 230201 «Информационные системы и технологии» очной формы обучения

Часть 4

A B

Воронеж 2012

Составители: канд. физ.-мат. наук В.В. Дежин, д-р техн. наук М.Л. Лапшина

УДК 517 Методические указания: Использование математического

моделирования при решении прикладных задач для организации самостоятельной работы по курсу «Математика» раздела «Теория вероятностей и математическая статистика» для студентов специальности 230201 «Информационные системы и технологии» очной формы обучения. Ч. 4 / ФГБОУВПО «Воронежский государственный технический университет»; сост. В.В. Дежин, М.Л. Лапшина. Воронеж, 2012. 52 с.

Методические указания предназначены в качестве руководства для самостоятельного изучения студентами специальности 230201 (ИС) очной формы обучения раздела «Теория вероятностей и математическая статистика» курса «Математика». Методические указания включают в себя 2 занятия и содержат ссылки на литературу, пояснения и примеры, контрольные вопросы и задачи, форму отчетности.

Предназначены для студентов четвертого семестра второго курса.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word и содержатся в файле ИС- вероятность-4.pdf.

Табл. 11. Библиогр.: 22 назв.

Рецензент канд. физ.-мат. наук, доцент В.В. Ломакин

Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© ФГБОУВПО «Воронежский государственный технический университет», 2012

ЗАНЯТИЕ № 10

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

10.1. Основные понятия

Функция распределения является универсальной характеристикой случайной величины, описывающей как дискретные, так и непрерывные случайные величины. Плотность распределения вероятностей описывает только непрерывную случайную величину. Но описание случайных величин функцией распределении или плотностью распределения вероятностей, являющимся самым полным и самым подробным описанием случайной величины, достаточно сложно. Даже несложные преобразования, такие как сложение, умножение, деление случайных величин приводят к достаточно сложным преобразованиям плотности распределения вероятностей, связанным с вычислением интегралов. Кроме того, эмпирическое определение функции распределения или плотности распределения вероятностей случайной величины требует очень большого числа измерений ее значений. В связи с этим возникает необходимость в другом описании случайных величин, пусть не столь полном и характеризующем лишь некоторые их свойства, но зато более простом и требующем меньшего числа измерений при проведении экспериментальных исследований, тем более, что во многих случаях нет необходимости характеризовать случайную величину полностью. Чаще всего достаточно указать только отдельные числовые параметры, достаточно хорошо характеризующие существенные черты распределения случайной величины. Такие характеристики, дающие в сжатой форме наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины. Существует большое количество различных числовых характеристик, имеющих различное назначение и различные области применения.

10.1.1.Характеристики положения случайной величины

Рассмотрим характеристики положения СВ, которые указывают число, около которого группируются все возможные значения СВ.

Важнейшей из характеристик положения, а именно среднего значения случайной величины, является математическое ожидание.

Математическим ожиданием (средним значением по распределению) называется действительное число, определяемое в зависимости от типа случайной величины X

формулой

Математическое ожидание существует, если ряд (соответственно интеграл) в правой части формулы (10.1) сходится абсолютно.

Приведем значения математических ожиданий для ДСВ и НСВ, рассмотренных в занятии № 9:

1)геометрическое распределение – M X 1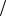p;

2)биномиальное распределение – M X np;

3)распределение Пуассона – M X ;

4)гипергеометрическое распределение – M X nM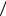N ;

5)равномерное распределение – M X a b ;

2

6)показательное распределение – M X 1 ;

7)нормальное распределение – M X m;

8)распределение Рэлея – M X 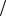2 ;

9)распределение по закону Симпсона – M X 0;

10)у распределения Коши математического ожидания не существует;

11)распределение Максвелла – M X 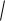22( ) ;

12)распределение по закону арксинуса – M X 0;

13)распределение Лапласа – M X m;

15)гамма-распределение – M X ab;

16)распределение хи-квадрат – M X n;

ожидания.

1.M C C (C const ), т.е. математическое ожидание постоянной равно этой постоянной.

2.M CX C M X , т.е. постоянную величину можно

выносить за знак математического ожидания.

3. Свойство аддитивности математического ожидания. Математическое ожидание суммы случайных величин равно сумме математических ожиданий при условии, что математические ожидания слагаемых конечны

M X Y M X M Y .

Свойство 3 остается справедливым и в том случае, когда одна из случайных величин дискретная, а другая – непрерывная.

Из свойств 2 и 3 вытекает

Следствие (свойство линейности математического ожидания) M C1X C2Y C1M X C2M Y , где C1 и C2 – постоянные.

4. Свойство мультипликативности математического ожидания. Если случайные величины X , Y независимы и M X , M Y конечны, то

M X Y M X M Y .

Это свойство, как и предыдущее, остается справедливым и тогда, когда одна из случайных величин дискретная, а другая непрерывная.

7. Математическое ожидание отклонения случайной величины X от ее математического ожидания равно нулю

MX M X 0.

8.Если a X b, то a M X b, где a и b – посто-

янные величины.

9. Абсолютная величина математического ожидания случайной величины всегда меньше или равна математическому ожиданию абсолютного значения случайной величины

M X M X .

Кроме математического ожидания в качестве характеристик положения случайной величины применяются медиана и мода.

Медианой Me X h X (срединным значением) назы-

вается действительное число, удовлетворяющее условию

Для дискретных случайных величин медиана определяется неоднозначно и практически не употребляется. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная графиком плотности распределения, делится пополам.

Модой Mo X d X случайной величины непрерыв-

ного типа называется действительное число, определяемое как точка максимума плотности распределения вероятностей fX x .

Модой Mo X d X (наивероятнейшим значением)

случайной величины дискретного типа определяется как та-

кое значение случайной величины, для которого

Таким образом, мода есть наиболее вероятное значение, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное или одномодальное распределение) или иметь множество значений (мультимо-

дальное или многомодальное распределение).

Квантилью порядка p распределения случайной величины X непрерывного типа называется действительное число tp , удовлетворяющее уравнению

В частности, из определения медианы следует, что h X t0,5.

Критической точкой порядка p распределения слу-

чайной величины X непрерывного типа называется действительное число p , удовлетворяющее уравнению

Квантиль и критическая точка одного и того же распределения связаны простым соотношением: p t1 p .

10.1.2. Характеристики разброса значений случайной величины

Математическое ожидание является центром группирования возможных значений случайной величины. Но для полной характеристики случайной величины необходимо знать степень разброса ее значений относительно центра группирования. Для этого вводятся характеристики рассеивания. Важнейшей из них является дисперсия.

Дисперсией случайной величины X называется число D X , равное математическому ожиданию квадрата от-

клонения случайной величины от ее математического ожидания:

Если известен закон распределения случайной величины, то из определении математического ожидания следуют формулы для вычисления дисперсии

Дисперсия существует, если ряд (соответственно интеграл) в правой части формулы (10.8) сходится абсолютно.

Из свойств математического ожидания и определения дисперсии имеем

D X M X M X 2 M X2 2X M X M2 X

M X2 2M X M X M2 X M X2 M2 X . (10.9)

Приведем значения дисперсий для ДСВ и НСВ, рассмотренных в занятии № 9:

1)геометрическое распределение – D X 1 p p2 ;

2)биномиальное распределение – D X npq;

3)распределение Пуассона – D X ;

4)гипергеометрическое распределение – D X N n

N 1

5)равномерное распределение – D X b a 212;

6)показательное распределение – D X 1 2 ;

7)нормальное распределение – D X 2;

8)распределение Рэлея – D X 2 2 2 ;

9)распределение по закону Симпсона – D X a2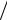6;

10)у распределения Коши дисперсии не существует;

11)распределение Максвелла – D X 3 8 ;

12)распределение по закону арксинуса – D X a22;

13)распределение Лапласа – D X 2;

ли a 2;

15)гамма-распределение – D X ab2 ;

16)распределение хи-квадрат – D X 2n;

Рассмотрим основные свойства дисперсии.

1.D X 0 для любой случайной величины X .

2.D C 0 (C const ), т.е. дисперсия постоянной величины равна нулю.

3.D CX C2D X , т.е. постоянную величину можно

выносить за знак дисперсии, возведя ее в квадрат.

4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий:

D X Y D X D Y .

Следствие свойств 3 и 4. Дисперсия разности случайных величин X и Y равна сумме их дисперсий:

D X Y D X D Y .

Свойство 4 обобщается на случай суммы любого конечного числа случайных величин: дисперсия суммы конечного числа попарно независимых случайных величин X1, X2, ,

Xn равна сумме их дисперсий

D X1 X2 Xn D X1 D X2 D Xn .

5. Дисперсия случайной величины не изменится, если к ней добавить постоянную величину, т.е.

D X C D X .

Дисперсия имеет размерность квадрата случайной величины. Для характеристики разброса часто удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Такой величиной является среднеквад-

ратическое отклонение.

Среднеквадратическим отклонением случайной величины X называется неотрицательное число X , равное

положительному значению квадратного корня из дисперсии случайной величины X :

10.1.3. Моменты

Для более полного описания случайной величины применяют еще ряд характеристик, среди которых чаще всего используются так называемые моменты. Различают начальные и центральные моменты.

Начальным моментом k -го порядка (k 1, 2, ) слу-

чайной величины X называется действительное числоk k X , равное математическому ожиданию случай-

ной величины Xk , если оно существует.

Из этого определения следует, что начальный момент первого порядка есть математическое ожидание случайной величины: 1 M X .

Центральным моментом k -го порядка (k 1, 2, )

случайной величины X называется действительное числоk k X , равное математическому ожиданиюk -й сте-

пени отклонения случайной величины от своего матема-

тического ожидания Xk , если оно существует.

Между начальными и центральными моментами существуют связывающие их соотношения. Например, раскрывая

X 1 2 X 2 2 1X 12 ,

X 1 3 X3 3 1X2 3 12X 13 ,

X 1 4 X4 4 1X3 6 12X2 4 13X 14 ,

получим:

2 M X 2 2 1X 12 2 12 ,

3 M X3 3 1X2 3 12X 13 3 3 1 2 2 13 ,4 M X 4 4 1X3 6 12X2 4 13X 14

4 4 1 3 6 12 2 3 14 .

Чем больше моментов случайной величины известно, тем более детальное представление мы имеем о ее законе распределения.

Если распределение симметрично относительно математического ожидания, то все центральные моменты нечетного порядка, если они существуют, равны нулю. Через центральный момент третьего порядка определяется коэффициент

асимметрии As X 3 X 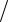3 X , характеризующий "ско-

шенность" распределения.

Через центральный момент четвертого порядка определя-

ется коэффициент эксцесса Ex X 4 X 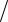4 X 3, ха-

рактеризующий "островершинность" распределения.

10.2. Примеры решения задач

Пример 1. Производятся последовательные независимые испытания пяти приборов на исправность. Исправность каждого из приборов равна 0,8. Каждый следующий прибор испытывается только в том случае, когда предыдущий оказался исправным. Найти закон распределения случайной величины X

– числа испытанных в данном эксперименте приборов, вычис-

лить M X , D X , X , Mo X , P 2 X 5 .

Решение. Очевидно, что X – ДСВ, причем ее возможные значения составляют множество 1, 2, 3, 4, 5 . Найдем соот-

ветствующие вероятности с помощью теорем сложения и умножения. P X 1 P {первый испытанный прибор оказался неисправным}=1-0,8=0,2. P X 2 P {первый испытанный прибор оказался исправным, а второй неисправным}=0,8·0,2=0,16. P X 3 P{первый и второй испытан-

ные приборы оказались исправными, а третий неисправ-

ным}=0,8·0,8·0,2=0,128. P X 4 P {первый, второй и тре-

тий испытанные приборы оказались исправными, а четвертый

второй, третий и четвертый испытанные приборы оказались исправными, а пятый может оказаться неисправным или ис-

правным}=0,8·0,8·0,8·0,8·(0,2+0,8)=0,4096. Запишем искомый закон распределения ДСВ X :

Контроль: 0,2+0,16+0,128+0,1024+0,4096=1.

Вычисляем математическое ожидание данной случайной величины:

MX x1p1 x2 p2 x3p3 x4 p4 x5 p5

1 0,2 2 0,16 3 0,128 4 0,1024 5 0,4096 3,3616.

Вычисляем дисперсию данной случайной величины:

D X M X2 M2 X

x12 p1 x22 p2 x32 p3 x42 p4 x52 p5 M2 X

11 0,2 22 0,16 32 0,128 42 0,1024 52 0,4096

3,36162 2,57.

Вычисляем среднеквадратическое отклонение:

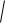X D X 2,57 1,6.

Мода данной случайной величины равна Mo X 5, так

как соответствующая вероятность p5 0,4096 максимальна.

Находим

P 2 X 5 P X 2 P X 3 P X 4

0,16 0,128 0,1024 0,3904.

Пример 2. Устройство состоит из 4 элементов, работающих независимо. Вероятность отказа любого элемента за время опыта равна 0,1. Найти закон распределения случайной величины X – числа отказавших элементов за время опыта, вычис-

лить M X , D X , X , Mo X , P 2 X 2 .

Решение. Очевидно, что X – ДСВ, причем ее возможные значения составляют множество 0, 1, 2, 3, 4 . Замечаем, что в

данном вероятностном эксперименте проводятся 4 повторных испытаний, причем

1)эти испытания независимы;

2)в каждом испытании два исхода – отказ и работа;

3)вероятность отказа в каждом испытании одинакова. Следовательно, мы имеем схему испытаний Бернулли с параметрами n 4 и p 0,1. Соответствующие вероятности нахо-

дим по формуле Бернулли:

P X 0 P4 0 C40 p0q4 1 0,10 0,94 0,6561; P X 1 P4 1 C41p1q3 4 0,11 0,93 0,2916 ; P X 2 P4 2 C42p2q2 6 0,12 0,92 0,0486; P X 3 P4 3 C43p3q1 4 0,13 0,91 0,0036; P X 4 P4 4 C44p4q0 1 0,14 0,90 0,0,0001.

Запишем искомый закон распределения ДСВ X :

Контроль: 0,6561+0,2916+0,0486+0,0036+0,0001=1.

Вычисляем математическое ожидание данной случайной величины:

M X x1p1 x2 p2 x3p3 x4 p4 x5 p5

0 0,6561 1 0,2916 2 0,0486 3 0,0036 4 0,0001 0,4.

Или, согласно формуле для биномиального распределения,

M X np 4 0,1 0,4.

Вычисляем дисперсию данной случайной величины:

D X M X2 M2 X

x12 p1 x22 p2 x32 p3 x42 p4 x52 p5 M2 X

02 0,6561 12 0,2916 22 0,0486 32 0,0036 42 0,0001

0,42 0,52 0,16 0,36.

Или, согласно формуле для биномиального распределения,

D X npq 4 0,1 0,9 0,36.

Вычисляем среднеквадратическое отклонение:

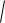X D X 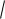0,36 0,6.

Мода данной случайной величины равна Mo X 0, так

как соответствующая вероятность p1 0,6561 максимальна. Находим

P 2 X 2 P X 0 P X 1

0,6561 0,2916 0,9477 .

Пример 3. Аппаратура состоит из 4000 элементов, каждый из которых независимо от остальных выходит из строя за время T с вероятностью 0,0005. Найти закон распределения случайной величины X – числа элементов, вышедших из строя за время T , вычислить M X , D X , X , Mo X ,

P 2 X 5 .

Решение. Очевидно, что X – ДСВ, причем ее возможные значения составляют множество 0, 1, 2, , 4000 . Замечаем,

что в данном вероятностном эксперименте проводятся 4000 повторных испытаний, причем

1) эти испытания независимы;

2)в каждом испытании два исхода – отказ и работа;

3)вероятность отказа в каждом испытании одинакова. Следовательно, мы имеем схему испытаний Бернулли с пара-

их произведение np 2 порядка единицы (0,1÷10), то для вычисления соответствующих вероятностей применима фор-

D X 2 1,41. Мода данной случайной величины име-

ет два значения: 1 и 2, так как соответствующие вероятности p2 p3 0,27067 максимальны. Находим

P 1 X 4 P X 2 P X 3

0,27067 0,18045 0,45112.

Пример 4. В партии из 10 деталей содержится 3 нестандартных. Наудачу отобраны 2 детали. Найти закон распределения случайной величины X – числа нестандартных деталей среди отобранных, вычислить M X , D X , X , Mo X ,

P 0 X 2 .

Решение. Очевидно, что X – ДСВ, причем ее возможные значения составляют множество 0, 1, 2 . Соответствующие

вероятности находим по формуле классической вероятности:

Запишем искомый закон распределения ДСВ X (гипергеометрическое распределение):

Таблица 4

Вычисляем математическое ожидание данной случайной величины:

Или, согласно формуле для гипергеометрического распределе-

ния, M X n M 2 3 0,6. N 10

Вычисляем дисперсию данной случайной величины:

D X M X2 M2 X x12 p1 x22 p2 x32 p3 M2 X

02 7 12 7 22 1 0,62 0,73 0,36 0,373. 15 15 15

Или, согласно формуле для биномиального распределения,

Вычисляем среднеквадратическое отклонение:

X D X 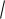0,373 0,61.

Мода данной случайной величины имеет два значения: 0 и 1, так как соответствующие вероятности p1 p2 7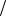15 максимальны.

Находим

P 0 X 2 P X 1 P X 2 7 1 8 0,533. 15 15 15

Пример 5. Два стрелка независимо друг от друга делают по одному выстрелу в мишень. Вероятности попадания в мишень для них соответственно равны 0,7 и 0,8. Найти закон распределения случайной величины X – разности числа попаданий в мишень первого и второго стрелка, вычислить M X ,

D X , X , Mo X , P 3 X 1 .

Решение. Очевидно, что X – ДСВ, причем ее возможные значения составляют множество 1, 0,1 . Найдем соответст-

вующие вероятности с помощью теорем сложения и умножения:

P X 1 P{первый стрелок промахнулся, а второй попал}=

1 0,7 0,8 0,24;

P X 0 P {оба стрелка промахнулись или оба попали}=

1 0,7 1 0,8 0,7 0,8 0,06 0,56 0,62;

P X 1 P {первый стрелок попал, а второй промахнулся}=

0,7 1 0,8 0,14.

Запишем искомый закон распределения ДСВ X : Таблица 5

Контроль: 0,24+0,62+0,14=1.

Вычисляем математическое ожидание данной случайной величины:

M X x1p1 x2 p2 x3p3 1 0,24 0 0,62 1 0,14 0,1.

Вычисляем дисперсию данной случайной величины:

D X M X2 M2 X x12 p1 x22 p2 x32 p3 M2 X

1 2 0,24 02 0,62 12 0,14 0,12 0,38 0,01 0,37 .

Вычисляем среднеквадратическое отклонение:

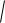X D X 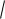0,37 0,61.

Мода данной случайной величины равна Mo X 0, так

как соответствующая вероятность p2 0,62 максимальна. Находим

P 3 X 1 P X 1 P X 0 0,24 0,62 0,86.

Пример 6. Длительность времени безотказной работы T элемента имеет показательное распределение, функция распределения которого

F t P T t 1 e t ( 0)

определяет вероятность отказа элемента за время длительностью t. Функцией надежностью R t называют функцию, оп-

ределяющую вероятность безотказной работы элемента за время длительностью t:

(10.15)

Доказать характеристическое свойство показательного закона надежности: вероятность безотказной работы элемента в интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности интервала t (при заданной интенсивности отказов ).