Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 659

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

515.92 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

ФГБОУ ВПО «Воронежский государственный технический университет»

Кафедра высшей математики и физико-математического моделирования

265 - 2013

КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ для организации самостоятельной работы

по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность»,

профили «Защитавчрезвычайныхситуациях», «Безопасностьжизнедеятельностивтехносфере», «Защитаокружающейсреды», очной формы обучения

Воронеж 2013

Составитель канд. физ.-мат. наук И.Н. Пантелеев

УДК 681.3.06

Криволинейные и поверхностные интегралы: методические указания для организации самостоятельной работы по курсу "Высшая математика" для студентов направления 280700.62 «Техносферная безопасность», профили «Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды», очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. И.Н. Пантелеев. Воронеж, 2013. 42 с.

Настоящие методические указания предназначены в качестве руководства для организации самостоятельной работы по курсу "Высшая математика" при изучении в 3 семестре раздела «Теория поля» для студентов специальностей ЧС, БЖ и ЗС. В работе приведен теоретический материал, необходимый для выполнения заданий и решения типовых примеров.

Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 2003 и

содержатся в файле Vmfmm_KrvPovInt _1.pdf.

Ил. 29. Библиогр.: 4 назв.

Рецензент канд. физ.-мат. наук, доц. В.В. Ломакин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

ФГБОУ ВПО «Воронежский государственный технический университет», 2013

1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ ПО ДЛИНЕ ДУГИ ( I рода)

Опорный конспект № 1

1) Понятие КИ 1p

О:	f x, y непр.			в D ,	AB D ,	AB
разбивается			на	Ai 1 Ai	длиной	li ,
i		, M1 i , ni li
i	1, n	, M1 i , ni li
f x, y dl				n	i , ni li .
f x, y dl			lim	f	i , ni li .
			max li 0 i 1

p x, y - линейная плотность AB
m f x, y dl - масса AB
2) Свойства КИ 1p
1°.	f1 x, y f2			x, y dl f1dl f2dl ;

	AB				AB	AB
2°.	cf x, y dl c f x, y dl , c const ;

	AB			AB
3°. L L1 L2				f x, y dl fdl fdl ;
			L		L1	L2
4°. dl l - длина L ;
	L
5°.	f x, y dl f x, y dl

	AB		BA
3) Вычисление КИ 1p
a)
a)	AB : x x t , y y t - непр. дифф. на ,


f x, y dl f x t , y t				x2 y2 dt ;

AB					a,b
b)
b)	AB : y y x - непр. дифф. на
f x, y dl b		f x, y x	1 y x 2 dx
	a
AB

1.1. Кривые в Rn . Задача о массе кривой.

Понятие криволинейного интеграла I рода

О: Кривой L в Rn				будем называть			множество точек
M x1, x2 ,..., xn Rn ,				координаты которых x1, x2 ,..., xn
заданы		как	функции			некоторого			параметра
t R : L		M Rn : x		x	t , x	x t ,..., x		x	t .
			1	1	2	2	n	n
Каждой	т. M L			соответствует				радиус-вектор
r M x1 tM , x2 tM ,..., xn tM .

Пример: Траектория АВ движения материальной точки в трехмерном пространстве в зависимости от времени t задается параметрическими уравнениями х = x(t), у = y(t), z = z(t), tA t tB .

В качестве параметра t обычно выбирается переменная, строго возрастающая при движении по кривой, тогда началу кривой соответствует наименьшее, концу — наибольшее значение параметра t . Такие кривые называют ориентированными.


О: Кривая	L : xi xi t ,		i				,	t , , называется
					1, n
непрерывной,	если	xi t ,	i			,		непрерывны на , ;
				1, n
гладкой, если	xi t	непрерывно						дифференцируемы на

n			2	0 .		Кривая L называется кусочно-
, и xi	t
i 1
гладкой, если состоит из конечного числа							кривых. Кривая
L называется замкнутой, если конец совпадает с началом
xi xi ,	i				.
		1, n
Рассмотрим в плоскости						XOY кривую
							AB длиной l и

предположим, что вдоль этой кривой распределена масса с линейной плотностью M f x, y . Требуется определить

массу	кривой					на n	частей точками
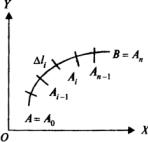
массу	кривой	AB . Разобьем			AB	на n	частей точками
A0 A, A1, A2 ,..., An B (рис.				1).	Обозначим		через	mi массу
						n
дуги	Ai 1 Ai	длиной	li ,	тогда		m mi .		Подсчитаем
						i 1
приблизительно массу дуги Ai 1 Ai .
				Рис. 1.1
			Пусть M i i , i				– произвольная
		точка Ai 1 Ai . Считая, что плотность в
		каждой точке дуги Ai 1 Ai такая же, как
		в т. Mi , получаем:
mi M i li i , i li . Суммируя, найдем
		n				n
		m	M i li i , i li .
		i 1			i 1

За точное значение массы кривой AB примем предел этой суммы при условии, что max li 0 . Итак,

m lim M i li . (1.1)

max l i 0 i 1

К подобного рода суммам и пределам приводят и другие задачи. Отвлекаясь от конкретного содержания приведенной задачи, рассмотрим непрерывную функцию f x, y ,

определенную в точках дуги
	AB . Составленная для нее сумма
n
f i , i li		(1.2)

i 1

называется интегральной.

О: Криволинейным интегралом от функции по длине AB называется предел интегральной суммы (1.2), если он существует, конечен и не зависит от способа разбиения

, и от выбора в них точек Mi , т.е.

,i 1, n

AB на части Ai 1 Ai

x, y dl lim

l .

(1.3)

max l

i i 1

Сравнивая (1.1) и (1.3), делаем вывод, что m x, y dl .

Аналогично

определяется

криволинейный

интеграл

f x1, x2 ,..., xn dl от функции переменных по длине

AB R

1.2. Свойства криволинейного интеграла I рода

Свойства криволинейного интеграла I рода (КИ Ip) приведены в ОК №1 и доказываются аналогично свойствам определенного интеграла с использованием (1.3). Специфическим по сравнению с определенным интегралом является свойство 5° неизменности КИ 1p при перемене ориентации кривой ( li 0 в (1.3) независимо от ориентации).

1.3. Вычисление криволинейного интеграла I рода

Криволинейный интеграл	f x, y dl легко сводится к

AB

определенному интегралу. Примем за параметр длину дуги l ,

отсчитываемую от	точки	A по			кривой
						AB , получим
параметрическое	представление					кривой
		*	, где l	*
AB : x x l , y y l , 0 l l					– длина дуги AB . Пусть

в (1.3) промежуточным точкам Mi i , i соответствует l li* , т.е. i x li* , i y li* . Тогда

		n			n
		f i , i li		f x li* , y li* li
		i 1			i 1
Последняя сумма является интегральной для определения
	l*
интеграла
интеграла		f x l ,	y l dl , т.е.
	0
			f x, y dl		l*
								(1.4)
						f x l	, y l dl .	(1.4)
					0
		AB
Эта формула доказывает существование криволинейного
интеграла I рода от функции				f x, y , непрерывной в D , если

AB D – непрерывная кусочно-гладкая кривая.

Рассмотрим формулы для вычислений криволинейного интеграла в следующих случаях:

	t , y y t , t , где	x t и
a) AB : x x
y t непрерывно дифференцируемые на , , тогда
dl	x t 2 y t 2 dt

т.е. из (1.4) имеем

2 dt .

x, y

, y

f x

Формула может быть обобщена на пространственный

случай, т.е. если

y y t , z z t , t ,

f x, y, z

непрерывна

AB : x x t ,

в D ,

, тогда

AB D

2 dt

x, y

, y

, z

Аналогичнозаписываетсяформуладлябольшегочислапеременных.

Пример:

x2 y2 dl ? L : x a cos t, y a sin t, 0 t 2

a2 cos2 t a2 sin2 t

y2 dl

a2 sin2 t a2 cos2 tdt

a3 dt 2 a3.

y x , a x b ,

где

y x непрерывно

AB :

дифференцируема на a,b , тогда

1 y x 2 dx

2 dx .

x, y

f x, y

y ln x,1 x 2 , если

Пример:

Найти

массу

кривой

линейная плоскость x, y x2 .

m x2dl 2

1 x2 dx 0,52

1 x2 1/ 2

d 1 x2

3/ 2

2 .

0,5

3 1 x

3 5

5 2

2. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ

(II РОДА)

Опорный конспект №2

1) Определение КИ 2р. Задача о работе

a P x, y ,Q x, y

P x, y ,Q x, y - непр. в D ,

D .

разбивается

на

Ai 1 Ai ,i

1, n

Ai 1 Ai

xi , yi , M i , i Ai 1 Ai

a dr Pdx Qdy

lim

x Q

max x, y 0

W Pdx Qdy F dr - работа силы

F P x, y ,Q x, y

на

dr dx, dy

2) Свойства КИ 2р

1°.

Pdx Qdy Pdx Qdy ;

2°. AB AC CB

Pdx Qdy Pdx Qdy Pdx Qdy ;

3°. D D1

D2 , D1 L1, D2

L2 , D L

Pdx Qdy

3) Вычисление КИ 2р

1)			t , y y t	- непр. дифф. на ,
1)	AB : x x		t , y y t	- непр. дифф. на ,

Pdx Qdy P x t , y t x t Q x t , y t y t dt

AB			x - непр. дифф. на a,b
2)
2)	AB : y y
Pdx Qdy b P x, y x Q x, y x y x dx
		a
AB
4) Связь между КИ 1р и 2р
LM - касательная к
LM - касательная к			AB в т. M ,

LM ,OX		, LM ,OY , LM ,OZ

P x, y, z dx Q x, y, z dy R x, y, z dz

P cos Q cos R cos dl

5) Формула Грина					P		Q
P x, y ,Q x, y	непр. в D вместе с				P	,	Q	,
					y		x
		Q	P
L D Pdx Qdy		Q	P	dxdy .
L D Pdx Qdy		x	y	dxdy .
L	D	x	y
		8

6) Условия		независимости	КИ 2р от контура
интегрирования
1.	Pdx Qdy 0 L* D
	L*
2.		Pdx Qdy не зависит от
2.		Pdx Qdy не зависит от		AB D

	AB

3.Pdx Qdy du,u u x, y D

4.P Q в Dy x

7) Интегрирование полных дифференциалов

Pdx Qdy du

	u x, y	x, y
	u x, y		Pdx Qdy c
		x0 , y0
	x		y
	c P x, y	dx Q x, y dy c
AC CB	x0		y0

2.1. Определение криволинейного интеграла II рода

Рассмотрим задачу о работе переменной силы. Пусть материальная точка под действием силы F P x, y ,Q x, y

перемещается вдоль кусочно-гладкой кривой

работу W силы F при перемещении точки А в В (рис.2.1). Для решения задачи

разобьем кривую AB на n частей точками A A0 , A1,..., An B . Заменим приближенно

на дуге силу	F значением	ее	в
т. Mi i , i Ai 1 Ai	, а движение по	Ai 1 Ai	-
	9

AB . Найти

Рис. 2.1

движением по отрезку Ai 1 Ai xi , yi . Тогда приближенное


значение	работы на		в силу справедливости формулы
		AB
W F s	(скалярное	произведение) для		F	const и

перемещения s находится по формуле

W n F M i Ai 1 Ai n P i , i xi Q i , i yi .

i 1

За точное значение работы естественно принять

lim

(2.1)

max x 0

max yii 0

i 1

Нахождение пределов сумм рассмотренного вида

встречается и в других задачах.

Рассмотрим теперь вектор a P x, y ,Q x, y , x, y D .

Разобьем кривую

на n частей и составим сумму

Q i , i yi .

P i , i xi

(2.2)

i 1

О: Криволинейным интегралом II рода (КИ 2р) по

координатам

от

функций

P x, y ,Q x, y

по

P x, y dx Q x, y dy - (обозначение),

называется

AB,

предел

интегральной

суммы

(2.2)

при

max xi 0, max yi

0 , если он не зависит от способа

разбиения AB на части и от выбора промежуточных точек

Mi , т.е.

P x, y dx Q x, y dy

lim

(2.3)

max x 0

max yii 0 i 1

	КИ 2р также называют интегралом от вектора по кривой и
обозначают			a d r, d r dx, dy .

			AB
	Если кривая L является замкнутой, ограничивающей
некоторую область D L D , то криволинейный интеграл по
замкнутому			контуру	называют циркуляцией и обозначается
			, причем положительным направлением обхода L
	F(x, y)	d r	, причем положительным направлением обхода L
L
считается то, при котором область D остается слева.
	Аналогично определяется криволинейный интеграл
			a dr			, если

			AB
					n
					n	, axi ax1 (x1, x2 ,..., xn ), i 1, n .
a	(ax1 , ax 2 ,..., ax n ), AB R					, axi ax1 (x1, x2 ,..., xn ), i 1, n .

2.2. Свойства криволинейного интеграла II рода

КИ 2р имеет свойства, аналогичные свойствам определенного интеграла. Наиболее важными из них являются:

1°. Pdx Qdy Pdx Qdy ;


AB	AB

2°. Pdx Qdy Pdx Qdy Pdx Qdy .


AB	AC	CB

3°. Пусть кривая L является замкнутой, ограничивающей некоторую область D. Если D D1 D2 (рис.2.2), D2 L2 , то

Рис.2.2

Pdx Qdy

Pdx Qdy Pdx Qdy .

(2.4)

В силу свойства 2°

Pdx Qdy

Pdx Qdy Pdx Qdy ,

AmB

Pdx Qdy

Pdx Qdy Pdx Qdy ,

BnA

складывая и учитывая 1°, получаем (2.4).

2.3. Вычисление криволинейного интеграла II рода

Пусть

причем

AB : x x(t), y y(t), t ,

x(t) , y(t)

непрерывно дифференцируемы на [ , ], т.е.

x(t), y(t) C1[ , ] . Тогда

P(x, y)dx Q(x, y)dy

(2.5)

(P(x(t), y(t))x (t) Q(x(t), y(t)) y (t))dt .

P(x, y)dx

Рассмотрим

lim

P( i , i ) xi

По

max x i 0 i 1

теореме

Лагранжа

(ti 1,ti ) .

xi x(ti ) x(ti 1 ) x (ti ) ti ,ti

Выберем

x(t* ),

y(t* ) ,

тогда

P( i , i ) xi

P(x(ti ), y(ti ))x (ti* ) ti .

i 1

В правой части полученного равенства – интегральная

сумма

для

определенного

интеграла

от

функции

Переходя

пределу при

max xi

0 ,

P(x(t), y(t))x

(t) .

получаем формулу (2.5).

Из вывода формулы (2.5)

для

существования КИ 2р

достаточно непрерывности f (x, y)

в D и гладкости AB .

Формула

(2.5)

может

быть обобщена

на

случай

, когда

a ax1 , ax2 ,..., axn , а

проекции

вектор-

AB R

функции

ax1

(x1, x2 ,..., xn ), ax n (x1, x2 ,..., xn )

непрерывны в и

уравнения, задающие

x1 (t), x2

x2 (t),..., xn xn (t),

–

AB : x1

непрерывно дифференцируемые функции при t .

В частности,

при

n 3, R3 (x x, x y, x z, a

P, a

x 2

Q, a

R) .

Pdx Qdy Rdz [P(x(t), y(t), z(t)x (t))

Q(x(t), y(t), z(t)) y (t) R(x(t), y(t), z(t))z (t)]dt .

Пусть

задана на плоскости:

y y(x), a x b ,

причем y y(x) – непрерывно дифференцируемая на [a,b]

функция. Тогда, считаем параметром, из (2.5) получаем

P(x, y)dx Q(x, y)dy [P(x, y(x)) Q(x, y(x)) y (x)]dx .

Примеры: 1. Найти работу силы

по

F { y, x, z}

перемещению материальной точки вдоль винтовой линии L :

x a cos t, y a sin t, z bt,0 t 2

W ydx xdy zdz

[ a sin t( a sin t) a cos t(a cos t) btb]dt

(a2 b2t)dt 2 (a2 b2 ).

2. Вычислить

(xy 1)dx x	2	ydy, A(1,0), B(0, 2),
			AB : 2x y 2 .

(xy 1)dx x2 ydy 0 [x(2 2x) 1) x2 (2 2x)( 2)]dx

	1
AB
	(x4 2x3 x2 x)	10 1.
	(x4 2x3 x2 x)	10 1.
	2.4. Связь между криволинейными
	интегралами I и II рода

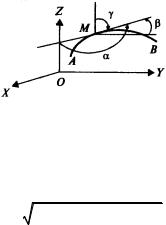
Рассмотрим пространственный случай. Обозначим через(x, y, z), (x, y, z), (x, y, z) углы, образованные касательной к

кривой AB в т. M (x, y, z) с осями OX ,OY ,OZ соответственно

(рис.2.3).

Рис. 2.3

Вектор dr(dx, dy, dz)				направлен по касательной к						в
									AB
т. M и cos	dx	,cos			dy	,cos	dz	.
	dr				dr		dr

				(dx)2 (dy)2			(dz)2 dl , имеем
Учитывая, что			d r
dx cos dl , dy cos dl ,							dz cos dl . Поэтому

P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz

(P cos Q cos R cos )dl.

Эта формула выражает связь между криволинейными

интегралами I и II рода.

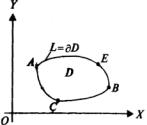
2.5. Формула Грина

Формула Грина устанавливает связь между криволинейным интегралом II рода и двойным интегралом.

Т:

Пусть

D R2 -

правильная

область,

ограниченная

гладкой

кривой

L D .

Функции

P(x, y),Q(x, y)

непрерывны

вместе с

частными

производными

, Q . Тогда справедлива формула Грина:

P(x, y)dx Q(x, y)dy ( Q

P)dxdy ,

причем кривая L обходится в положительном направлении.

Рассмотрим

Пусть

y (x)

– уравнение

P dxdy .

2 (x)

кривой

ACB ,

– уравнение кривой AEB ,

a x b

(рис. 2.4). Тогда

P dxdy b

P dy

b dx(P(x, y))

2 ( x)

dx 2

1 ( x)

b (P(x, 2 (x)) P(x, 1 (x))dx

P(x, y)dx

P(x, y)dx P(x, y)dx .

BEA

ACB

Аналогично, рассматривая кривые

CAE

и CBE , будем иметь

Q dxdy Q(x, y)dy .

Вычитая

из

этого

равенства

предыдущее,

получим

формулу

Рис. 2.4

Грина.

Замечание. Если область D не является правильной, то формула остается справедливой, так как D можно разбить на правильные части, применить формулу Грина к каждой из них и затем воспользоваться свойствами 3° для двойных интегралов и криволинейных интегралов II рода.

2.6.Условия независимости криволинейного интеграла

IIрода от пути интегрирования

В некоторых случаях величина КИ 2р не зависит от пути интегрирования, а зависит лишь от начальной и конечной точек A и B . Выясним, при каких условиях это справедливо.

Будем рассматривать односвязные области D R2 , т.е. такие, в которых для любого замкнутого контура L * , лежащего внутри D , ограниченная L * часть плоскости состоит целиком из внутренних точек D .

Т: Пусть функции P(x, y), Q(x, y) непрерывны вместе со своими частными производными Py , Qx в замкнутой

односвязной области D . Тогда следующие четыре условия эквивалентны:

1. Для любой замкнутой гладкой кривой справедливо

Pdx Qdy 0 .

2. Для любых точек A, B D значение

Pdx Qdy не зависит от пути
Pdx Qdy не зависит от пути	AB D .

AB

3.Pdx Qdy du, u u(x, y), (x, y) D .

4.P Q в D .y x

Достаточно доказать, что 1 2 3 4 1.

1 2: Используя свойства 1°, 2° КИ 2р, имеем (рис.2.5)

Рис.2.5

Pdx Qdy 0 Pdx Qdy

Pdx Qdy 0

AnB

AmB

Pdx Qdy Pdx Qdy .

AnB

AmB

2 3: Пусть

A(x0 , y0 ), B(x, y) D ,

тогда

Pdx Qdy

( x, y)

является функцией от x, y , т.е. u(x, y)

Pdx Qdy .

( x0 , y0 )

u(x, y) ,

Чтобы

показать

дифференцируемость

т.е.

du Pdx Qdy ,

достаточно

доказать

существование

для

(x, y) D

частных

производных

u P,

u Q .

По

определению частной производной

u(x x) u(x, y)

Pdx Qdy Pdx Qdy

lim

x 0

Pdx Qdy

lim

x 0

где т. C(x x, y) , причем в силу условия эквивалентности 2-й путь от B до C можно взять

прямолинейным:		y const (рис.2.6).
Тогда			x x

u	lim		P(x, y)dx
			x
x			x
	x 0

Рис. 2.6

и по теореме о среднем для определенного интеграла получаем

u		P( , y) x	x x x
	lim
x		x
	x 0		x при x 0

lim P( , y) P(x, y) .

Аналогично доказывается равенство uy Q(x, y) .

3 4: Из условия 3 следует, что по теореме о равенстве частных производных высших порядков, отличающихся

порядком дифференцирования

x y

y x

4 1: Пусть

гладкая

замкнутая

кривая L* D

ограничивает

область

D* D

(в

силу

односвязности

D ).

Тогда по формуле Грина

Pdx Qdy

dxdy 0 .

2.7. Интегрирование полных дифференциалов

Пусть выражение

P(x, y)dx Q(x, y)dy

является полным

дифференциалом

некоторой

функции

u(x, y) .

Из

доказательства

условий независимости

криволинейного

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022514.54 Кб3Учебное пособие 654.pdf
#
30.04.2022514.96 Кб2Учебное пособие 655.pdf
#
30.04.2022515.3 Кб6Учебное пособие 656.pdf
#
30.04.2022515.55 Кб3Учебное пособие 657.pdf
#
30.04.2022515.73 Кб4Учебное пособие 658.pdf
#
30.04.2022515.92 Кб3Учебное пособие 659.pdf
#
30.04.2022258.19 Кб6Учебное пособие 66.pdf
#
30.04.2022516.14 Кб4Учебное пособие 660.pdf
#
30.04.2022517.28 Кб2Учебное пособие 661.pdf
#
30.04.2022519.69 Кб4Учебное пособие 662.pdf
#
30.04.2022521.51 Кб1Учебное пособие 663.pdf