Учебное пособие 630
.pdfЛАБОРАТОРНАЯ РАБОТА № 2 ИССЛЕДОВАНИЕ АМПЛИТУДНО-ФАЗОВЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ САР
1. ЦЕЛЬ РАБОТЫ
Целью работы является ознакомление с амплитуднофазовыми частотными характеристиками (АФЧХ) линейных динамических звеньев САР, изучение годографов комплексных коэффициентов передачи (ККП) для элементарных звеньев и исследование влияния отдельных параметров звеньев на поведение и устойчивость системы.
2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Выражениями для передаточных функций элементарных звеньев, исследованных при выполнении лабораторной работы № 1:
Для интегрирующее звена:
|
W ( p) = |
k |
|
|
|
|
|
p |
|
||||
|
|
|
|
|||
|
Для дифференцирующего звена: |
|
||||
|
W ( p) = kp |
|
||||
Для инерционного (апериодического) звена: |
|
|||||
|
W ( p) = |
|
k |
|
|
|
|
Tp +1 |
|
||||
|
|
|
||||
|
Для форсирующего звена |
|
||||
|
W ( p) = K (Tp +1) |
|
||||
Для перехода от операторной формы передаточной |
||||||
функции (ПФ) к комплексному |
коэффициенту |
передaчи |
||||
(ККП), |
определяющему амплитудно-фазовую |
частотную |
||||
11
ПФ |
Тогда получим: = √−1 |
|
|
|
|
|||
характеристику звена (АФЧХ), следует в выражениях для |
||||||||
|
принять p=jω где |
|
|
|
– мнимая единица |
|
||
|
для интегрирующего звена: |
|
||||||
|
W ( jω) |
= |
|
k |
|
(1) |
||
|
|
jω |
||||||
|
|
|
|
|
|
|||
|
для дифференцирующего звена: |
|
||||||
|
W ( jω) = k( jω) |
(2) |
||||||
|
для инерционного (апериодического) звена: |
|
||||||
|
W ( jω) = |
|
|
|
k |
(3) |
||
|
|
T ( jω) +1 |
|
|||||
для форсирующего звена:
W ( jω) = k[Tjω +1] |
(4) |
Для перехода к амплитудным и фазовым частотным характеристикам в (1 - 4) следует перейти сначала к алгебраической форме с выделением действительной и мнимой частей, а затем - к экспоненциальной форме представления комплексных функций:
W ( jω) = u(ω) + jv(ω) |
(5) |
W ( ϕω) = A(ω)e− ϕϕ(ω) |
(6) |
12
где A(ω) |
- модуль |
ККП |
|
(амплитудная |
частотная |
|
характеристика звена), |
|
|
|
|
||
ϕ(ω) - аргумент |
ККП |
(фазовая |
частотная |
|||
характеристика звена), |
|
|
|
|
||
|
|
(7) |
|
|||
A(ω) = u 2 (ω) + v2 (ω) |
|
|||||
ϕ(ω) = arctg |
υ(ω) |
|
(8) |
|
||
|
|
|
υ(ω) |
|
|
|
Функция |
arctg(ω) |
- |
нечётная |
значит, |
||
arctg(−ω) = −arctg(ω) |
|
|
|
|
||
Годограф ККП - траектория движения конца вектора ККП в полярной системе координат, при изменении частоты ω от 0до + ∞
При нахождении ККП уравнение необходимо привести к виду W ( jω) = u(ω) + jv(ω)
3. ЛАБОРАТОРНЫЕ ЗАДАНИЯ
Лабораторное задание: Исследовать ЛАЧХ и ЛФЧХ
универсального звена W ( p) = k( pT1 +1) , где pT2 +1
13
k – коэффициент усиления операционного усилителя Т1 – постоянная времени формирующего звена Т2 – постоянная времени инерционного звена
4. КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ПРОДЕЛАННОЙ РАБОТЕ
1)что такое комплексный коэффициент передачи (ККП) для САР и ее звеньев? Какова связь между ККП и ПФ?
2)какова связь между амплитудно-частотными характеристиками (АЧХ), фазово-частотными характеристиками (ФЧХ) и ККП?
3)какова методика определения АЧХ и ФЧХ?
4)для чего используются асимптотические логарифмические частотные характеристики?
5)что такое годограф ККП? Для чего он используется?
6)как его построить?
14
ЛАБОРАТОРНАЯ РАБОТА № 3 ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ САР
1. ЦЕЛЬ РАБОТЫ
Закрепление теоретических знаний и приобретение практических навыков анализа устойчивости замкнутых систем регулирования по их линейным моделям с использованием критерия Найквиста-Михайлова; изучение влияния на устойчивость систем параметров динамических звеньев САР.
2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
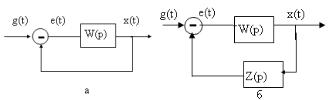
Критерий устойчивости Найквиста-Михайлова основан на рассмотрении частотных характеристик разомкнутых САР и вытекает из принципа аргумента. Передаточная функция САР, имеющей единичную обратную связь (ОС) (рис. 1, а), имеет вид
K ( p) = |
W ( p) |
(1) |
|
1 +W ( p) |
|||
|
|
где W(р) - передаточная функция разомкнутой САР
Рис. 1
При неединичной ОС (рис. 1, б)
15
K ( p) = |
W ( p) |
(2) |
1 + Z ( p) W ( p) |
Поскольку в лабораторной работе исследуются только системы с устойчивыми и нейтральными динамическими звеньями, то критерий устойчивости может быть сформулирован следующим образом:
Если годограф разомкнутой линейной системы не охватывает точку с координатами (-1; j0), то соответствующая этой системе замкнутая система, полученная путем замыкания единичной обратной связи, будет устойчива.
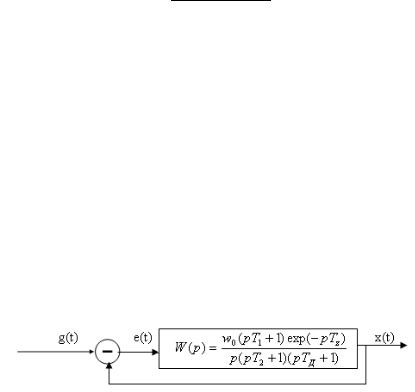
3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИССЛЕДУЕМОЙ СИСТЕМЫ
Структурная схема анализируемой системы приведена на рис. 3.
Рис. 3
Как видно из рис. 3, система имеет сложную передаточную функцию, поэтому вначале следует провести исследование годографов элементарных звеньев, входящих в передаточную функцию в виде сомножителей. Для передаточной функции вида
W ( p) = w0 ( pT1 +1) exp(−pTz ) |
(3) |
|||
p( pT |
+1)( pT |
Д |
+1) |
|
2 |
|
|
|
|
16
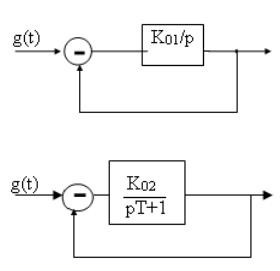
Такими простейшими звеньями являются:
-к0 - пропорциональное звено;
-exp(-pTz) - идеальное звено задержки (запаздывания сигнала) на время Tz;
-кp0 - интегрирующее звено (используется в
системе ФАП);
|
к02 |
|
|
- |
|
- инерционное звено (используется в |
|
pT +1 |
|||
системе ЧАП) |
|
|
|
- W ( p) = к03 ( pT +1) - форсирующее |
звено |
||
(используется как корректирующее). |
|
||
Рис. 4
Рис. 5
В процессе работы необходимо уметь определять характерные точки годографа: частоты среза и сопряжения частотно-фазовых характеристик, критические частоты. Ниже приведен пример расчета характерных точек и построения
17
годографа для системы третьего порядка с передаточной функцией вида
|
W ( p) = |
к0 |
|
(4) |
|
pT +1 |
|||
|
|
|
||
1. |
Частота среза |
замкнутой |
системы находится из |
|
соотношения |W(jω)|=1
АЧХ = Аω = W ( jω) =1
W ( jω) =1
|
|
W |
|
|
=1 |
|
|
|
|
|
|
|
|
|
T 2ωср2 |
+1 |
||||
|
|
|||||
u 2 |
=T 2ωср2 +1 |
|||||
ω |
2 |
= |
W 2 −1 |
|||
ср |
|
T 2 |
||||
|
|
|
||||
|
|
|
|
|||
(5) (6)
(7)
(8)
(9)
|
ωср = |
|
W 2 −1 |
|
|
|
(10) |
|
|
T |
|
|
|
||
|
|
|
|
|
|
|
|
2. |
Набег фазы на частоте среза равен |
|
|||||
|
ϕ(ωср ) = ФЧХ |
(ωср ) = arctg |
v(ωср ) |
|
(11) |
||
|
u(ωср ) |
||||||
|
|
|
|
|
|
||
3. |
Запас устойчивости по фазе ϕзап |
для замкнутой |
|||||
системы
ϕзап = −Π −ϕ(ωср) = −Π + arctg(
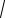k 2 −1) (12)
18
При выполнении лабораторных заданий годографы строятся автоматически, с помощью программы, однако изображения векторов и характерных точек на экране не воспроизводятся.
Замечание: при анализе устойчивости по годографу разомкнутой системы следует обратить внимание на определение “охватываемости” годографом точки (-1; j0): необходимо всегда идти из начала координат вправо по
действительной оси до точки начала годографа (ω=0), либо ”до бесконечности”, затем следует идти по линии годографа, либо по окружности “бесконечного радиуса” до встречи с другой
ветвью годографа, а затем по линии годографа к точке ω=∞ , как это показано на рис. 7, 8.
Рис. 7
Рис. 8
19
4. ЛАБОРАТОРНЫЕ ИССЛЕДОВАНИЯ ВЛИЯНИЯ ДОПОЛНИТЕЛЬНЫХ ЗВЕНЬЕВ НА УСТОЙЧИВОСТЬ
ПРОСТЕЙШИХ СИСТЕМ
4.1. Влияние звеньев на устойчивость системы первого порядка с одним инерционным звеном
4.1.1. Задание первое. Исследовать влияние на устойчивость звена идеальной задержки (запаздывание сигнала в системе).
Указания по выполнению
Установить значение усиления к0=2, постоянную времени Т2 согласно индивидуальному заданию, а остальные постоянные времени установить равными нулю. Построить
годограф звена. Определить частоту среза ωср и запас
устойчивости по фазе ϕзап в замкнутой системе, пользуясь методикой, проиллюстрированной на примере рис. 6 ,для
полученной САР (W ( p) = |
к0 |
|
|
). |
|
pT +1 |
||
|
2 |
|
Рассчитайте допустимое время запаздывания сигнала в замкнутой системе Тз доп. Введите это значение времени задержки в программу. Постройте годограф системы с запаздыванием. Сделайте вывод о потере устойчивости системы при Тз больше допустимого.
4.1.2. Задание второе. Исследовать влияние форсирующего звена (коррекция системы)
Указания по выполнению. Введите в потерявшую устойчивость систему дополнительное форсирующее звено с частотной характеристикой
W(jω)=1+jωT1, приняв Т1=0,1 с. Постройте годограф скорректированной системы.
20