
Матрицы и определители. методические указания для практических и самостоятельных работ по дисциплине «Элементы высшей математики». Хошимова Ф.Ф
.pdf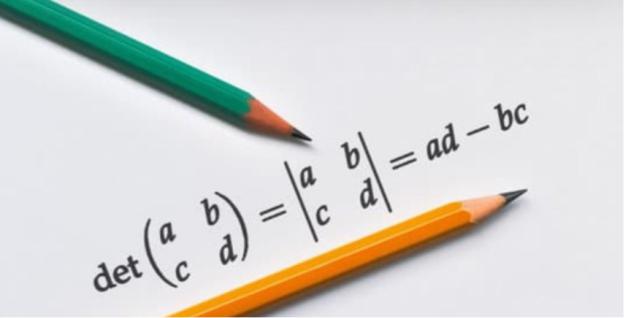
МАТРИЦЫ
И
ОПРЕДЕЛИТЕЛИ
Методические указания для практических и самостоятельных работ по дисциплине
«Элементы высшей математики» для студентов 1-го и 2-го курса всех специальностей
Воронеж 2021
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Строительно-политехнический колледж
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
Методические указания для практических и самостоятельных работ
по дисциплине «Элементы высшей математики» для студентов 1-го и 2-го курса
всех специальностей
Воронеж 2021
УДК 512.63(07) ББК 22.143я7
Составитель Ф.Ф. Хошимова
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ: методические указания для практических и самостоятельных работ по дисциплине «Элементы высшей математики» для студентов 1-го и 2-го курса всех специальностей / ФГБОУ ВО «Воронежский государственный технический университет»; сост. Ф. Ф. Хошимова. – Воронеж: Изд-во ВГТУ, 2021. – 22 с.
Методические указания включают основные понятия и определения части раздела элементов линейной алгебры, приводятся примеры решения задач с использованием различных методов нахождения определителя, обратной матрицы и ранга матрицы, а также представлены задания для самостоятельной работы и контрольные вопросы по теме.
Предназначены для студентов среднетехнического образования 1-го и 2- го курсов всех специальностей.
Методические указания подготовлены в электронном виде и содержатся в файле МУ ЛРУ (2) pdf.
Библиогр.: 3 назв.
УДК 512.63(07) ББК 22.143я7
Рецензент – Л. В. Стенюхин, кандидат физико-математических наук, доцент кафедры прикладной математики и механики ВГТУ
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ВВЕДЕНИЕ
Дисциплина «Элементы высшей математики», которая входит в основу профессиональной образовательной программы, относится к математическому и общему естественнонаучному циклу учебного плана.
Каждое начало имеет своё фундамент, и как раз высшее математическое образование начинается с изучения раздела линейной алгебры, в которую входит теория матриц.
Целью методических указаний является формирование умения выполнять арифметические действия с матрицами, находить определители матриц, обратную матрицу и ее ранг.
Вметодических указаниях изложены основные формулы и понятия, включающие в себя умение и навыки в нахождении матрицы, а также вычисление определителя, обратной матрицы и ранга матрицы. Приведены различные методы, способы решения по конкретным правилам и свойствам матрицы, а также представлен ряд заданий для практического и самостоятельного решения, с образцом выполненного задания.
Вматематике часто сталкиваются с решением задач, представленных в виде таблиц чисел и называемых матрицами. На самом деле, матрицы удобно применять для решений многих задач компьютерной графики, операции с векторами или же, например, систем линейных уравнений, состоящих из нескольких уравнений для которого необходимо громоздкий способ решения обычным методом. Иными словами, матрица – эта наша первая ступенька к освоению линейной алгебры.
Общее положение и рекомендации при изучении темы
Целям и задачами самостоятельной работы студентов являются ознакомление с матричной символикой и основными понятиями алгебры матриц, а также научиться уверенно оперировать с матрицами.
Практическая и самостоятельная работа студентов помогает приобретать навыки и умения решения задач приёмами аналитической деятельности, а также формирует абстрактное представление логики мышления, что необходимо для осуществления межпредметных связей.
Пояснительная записка
Требования к результатам освоения дисциплины.
В результате освоения дисциплины обучающийся должен уметь:
–У1. Выполнять операции над матрицами и решать системы линейных уравнений;
–У2. Решать задачи, используя уравнения прямых и кривых второго порядка на плоскости;
3
– |
У3. Применять методы |
дифференциального и |
интегрального исчисления; |
|
|
–У4. Решать дифференциальные уравнения;
–У5. Пользоваться понятиями теории комплексных чисел. В результате освоения дисциплины обучающийся должен знать:
– З1. Основы математического анализа, линейной алгебры и аналитической геометрии;
–З2. Основы дифференциального и интегрального исчисления;
–З3. Основы теории комплексных чисел.
В результате освоения дисциплины обучающийся должен иметь
практический опыт: |
|
|
|
– |
П1. |
Использования |
информационно-коммуникационных |
технологий в своей профессиональной деятельности. |
|||
– |
П2. Создания стандартного продукта письменной коммуникации. |
||
Изучение дисциплины направлено на формирование у обучающихся |
|||
следующих общих компетенций: |
|
||
– |
ОК 01. Выбирать способы |
решения задач профессиональной |
|
деятельности, применительно к различным контекстам. |
|||
– |
ОК 02. Осуществлять поиск, анализ и интерпретацию информации, |
||
необходимой для выполнения задач профессиональной деятельности.
Практическая и самостоятельная работа
Практика играет главную роль в организации учебно-воспитательного процесса, цель которого заключается в развитии умственных навыков студентов и применение ими полученных теоретических знаний. Существенным фактором математического образования является умение решать задачи, понимать их смысл и сущность, владеть методами и правилами их вычисления.
Целью выполнения самостоятельной работы по дисциплине: «Элементы высшей математики», является умение работать с самим собой, работать над своими ошибками в процессе освоения данной темы.
В ходе выполнения самостоятельной и практической работы ставятся следующие задачи:
•Разбор имеющих в учебно-методическом комплексе решений задач с ответами;
•Применения основных методов, правил и свойств в процессе выполнения практических и самостоятельных заданий;
•Закрепление теоретических знаний, полученных в процессе лекционных занятий;
•Совершенствование навыков, необходимых для успешного решения задач по математике;
4

•Формирование профессионально-значимых качеств будущего специалиста.
МАТРИЦЫ
Основные понятия матрицы
Матрицей называется прямоугольная таблица чисел (аij элементов), состоящая из m-строк и n- столбцов, которую записывают в следующем виде:
a11 |
a12 |
... |
a1n |
|||
|
|
|
... |
|
|
|
a21 |
a22 |
a2n |
||||
A = |
... |
... ... ... |
. |
|||
|
|
|||||
|
|
|
|
|||
|
|
am2 |
... |
|
|
|
am1 |
amn |
|||||
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C, ….
Числа, составляющие матрицу, называются элементами матрицы. Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например, aij,
где i - номер строки, j - номер столбца. Приведем пример матрицы 2 на 2:
1 0 А = 2 5
Вы видите, что a11 = 1, a12 = 0, a21 = 2, a22=5 Обозначение для матриц:
–скобка (…) или […];
–знак равно |
Виды матриц 1) Квадратной матрицей называется матрица, у которой количество
строк равно количеству столбцов (размера n×n), число n называется порядком матрицы (m=n)
4 |
1 |
-7 |
|
-1 |
0 |
2 |
- квадратная матрица размера 3×3 |
|
|||
4 |
6 |
7 |
|
2) Матрица называется прямоугольной, если количество строк не равно количеству столбцов (m≠ )
|
3 |
−1 |
0 |
|
B = |
|
|
|
|
|
2 |
3 |
5 |
|
|
|
5

3) Нулевой матрицей называется матрица, все элементы которой равны нулю, т.е. aij = 0.
|
0 |
0 |
0 |
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
4) Матрица, содержащая 1 строку или столбец, называется вектор (вектор-строка или вектор-столбец)
1 |
4 |
-5 |
- векторстрока |
|
8
-7 - вектор-столбец
3
5) Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю. (главная и побочная)
|
3 |
0 |
0 |
|
|
0 |
−1 |
0 |
|
|
|
|||
|
0 |
0 |
2 |
|
|
|
6) Единичной матрицей (Е) называется диагональная матрица, диагональные элементы которой равны 1.
|
1 |
0 |
0 |
|
|
|
0 |
1 |
0 |
|
= E |
|
|
||||
|
0 |
0 |
1 |
|
|
|
|
|
7) Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
• Верхней треугольной матрицей называется матрица, все элементы которой ниже главной диагонали равны нулю.
Пример верхней треугольной матрицы.
|
1 |
1 |
− 8 |
|
|
0 |
5 |
3 |
|
|
|
|||
|
0 |
0 |
0 |
|
|
|
• Нижней треугольной матрицей называется матрица, все элементы которой выше главной диагонали равны нулю.
6
Пример нижней треугольной матрицы.
|
1 |
0 |
0 |
|
|
6 |
1 |
0 |
|
|
|
|||
|
− 2 |
0 |
5 |
|
|
|
• Транспонированная матрица – это преобразованная матрица, при котором её строки становятся столбцами с теми же номерами, а столбцы − строками. Обозначение: АТ.
Пример: |
|
|
|
|
|
|
|
|
2 |
0 |
|
|
2 |
−1 |
|
|
|
|
|
|
|||
А = |
|
|
; АТ |
= |
|
|
; |
|
−1 |
3 |
|
|
0 |
3 |
|
|
|
|
|
||||
• |
Ступенчатой |
|
матрицей называется матрица, при котором |
||||
выполняются следующие условия:
Первое: удовлетворение условия при а11>0, т.е. число, стоящее в 1 строке и в 1 столбце должно быть не равным нулю, если а11=0, то преобразуем матрицу путём элементарных преобразований:
1.Перемена местами двух строк(столбцов).
2.Умножение строки(столбца) на число, отличное от нуля.
3.Прибавление к элементам одной строки(столбца) соответствующие элементов другой строки(столбца).
Второе: Все элементы матрицы под крайним элементом первой строки первого столбца (а11) делаем нулевыми. Тоже самое проводим простейшие операции относительной второй, третьей и т.д. строки так, чтобы образовалась визуально некая ступенька.
Третий этап: проверка удовлетворения условий
Пример:
|
1 |
4 |
− 2 |
2 |
|
|
0 |
2 |
3 |
7 |
|
|
|
||||
А = |
0 |
0 |
− 7 |
9 |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
7

|
−1 |
|
1 |
|
|
|
|
|
|
|
|
|
A = |
0 |
|
4 |
|
1. |
|
2 |
|
1 |
|
|
|
|
|||
2. |
0 |
−3 |
|||
A = |
|
|
|
||
|
|
|
1 |
|
|
|
2 |
|
|||
Задание для выполнения практической работы
Найти транспонированную матрицу:
|
|
0 |
|
|
|
|
|
|
|
|
|
|
A = |
2 |
|
|
|
|
|
|
|
|
|
3. |
|
−1 |
|
|
|
|
|
|
|
|
|
4. |
|
1 |
2 |
3 |
|
A = |
|
|
|
|
|
|
|
4 |
5 |
6 |
|
|
|
|
|||
Привести матрицу к ступенчатому виду:
|
|
|
1 |
|
0 |
−1 −1 |
|
1 |
|
0 |
−1 |
−1 5×I+III |
|
||||||
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
3 |
|
− 2 −1 0 II − 3 I ~ |
0 |
− 2 |
2 3 |
|
~ |
~ |
|||||||||
|
|
|
|
− 5 |
3 |
|
|
|
− 5 |
3 |
|
|
|
|
|
|
|||
|
|
|
|
2 −1 |
|
|
2 −1 |
|
|
||||||||||
1 0 −1 |
|
−1 |
|
|
1 0 |
|
−1 −1 |
|
|
|
|
||||||||
|
0 − 2 |
|
2 |
|
3 |
|
2×III+3×II |
|
0 − 2 |
|
|
|
|
|
|
|
|||
~ |
|
|
|
~ |
2 |
3 |
|
|
|
|
|
||||||||
|
0 3 |
|
− 3 |
|
− 6 |
|
|
|
|
0 0 |
|
0 − 3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 3 |
− 2 |
|
|
|
2 |
3 − 2 3 |
|
|
|
||||||||
|
2. |
|
|
|
|
|
|
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
3 1 |
1 |
. |
|
|
3 |
1 1 2 |
|
|
|
|
|||||||
|
|
|
1 5 |
− |
5 |
|
|
|
|
|
1 |
5 −5 4 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Выполнение действий над матрицами
Сложение и вычитание
Операция сложения (вычитания) матриц выполняется для матриц одинаковых размеров (число строк и столбцов одной матрицы должны быть равны другой).
Чтобы найти сумму матриц, необходимо сложить элементы с одинаковыми индексами (стоящие на одинаковых местах):
8
|
a |
a |
|
... |
a |
|
|
b |
b |
|
... |
b |
|
|
||
|
|
11 |
12 |
|
|
1n |
|
|
|
11 |
12 |
|
1n |
|
||
A + B = |
a21 |
a22 |
|
... |
a2n |
|
+ |
b21 |
b22 ... |
b2n |
= |
|||||
|
... |
... ... ... |
|
|
... |
... ... ... |
|
|||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
am2 |
|
... |
|
|
|
|
|
bm2 ... |
|
|
|
||
|
am1 |
|
amn |
|
bm1 |
bmn |
|
|||||||||
|
a |
+ b |
|
a |
+ b |
|
|
|
... |
a |
+ b |
|
|
|
||
|
|
11 |
11 |
|
12 |
12 |
|
|
1n |
|
1n |
|
|
|
||
|
a21 + b21 |
|
a22 + b22 ... |
a2n + b2n |
|
|
||||||||||
= |
|
... |
|
|
... |
|
|
|
... |
|
... |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
+ bm1 |
am2 + bm2 ... |
|
|
|
|
|
|
||||||
|
am1 |
amn + bmn |
|
|
||||||||||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 −3 |
0 |
|
3 |
3 −1 |
|
5 |
0 −1 |
|
|
|
||||||
A+ B = |
|
|
+ |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
4 5 |
|
|
− 2 −5 4 |
|
|
|
0 10 |
|
|
|
|
||||
|
6 |
|
|
|
2 |
|
|
|
|
|||||||
Аналогично определяется разность матриц. Умножение матрицы на число.
Любую матрицу можно умножить на любое число, при этом все элементы матрицы умножаются на это число.
a |
a |
|
... |
a |
|
|
ka |
ka |
... |
ka |
|
|||||
|
|
11 |
12 |
|
... |
|
1n |
|
|
|
11 |
12 |
... |
1n |
||
a21 |
a22 |
|
a2n |
|
ka21 |
ka22 |
ka2n |
|||||||||
k A = k |
... ... ... ... |
|
= |
... |
... ... ... |
. |
||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
am2 |
|
... |
|
|
|
|
|
|
|
kam2 |
... |
|
|
am1 |
|
amn |
|
kam1 |
kamn |
|||||||||||
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 А = 2 |
|
2 |
0 |
|
|
4 |
|
|
0 |
|
|
|
|
|
||
|
|
|
= |
|
|
|
|
|
. |
|
|
|
|
|||
|
|
|
−1 |
3 |
|
|
− 2 |
|
6 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
Произведение матриц
Произведение матриц можно определить если выполняется условие, при котором число строк первой матрицы должны совпадать с числом столбцов второй матрицы, так как при произведении двух матриц (например, АВ) 1-ая строка матрицы А прикладывается к первому столбцу матрицы В, соответствующие элементы перемножаются, а произведения складываются.
9
