Учебное пособие 437

ФГБОУВПО «Воронежский государственный технический университет»

Кафедра высшей математики и физико-математического моделирования

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ПРИ РЕШЕНИИ ПРИКЛАДНЫХ ЗАДАЧ

для организации самостоятельной работы по курсу «Математика» для студентов специальности 230201 «Информационные системы и технологии»

очной формы обучения

Часть 1

A B

Воронеж 2011

Составители: канд. физ.-мат. наук В.В. Дежин, д-р техн. наук М.Л. Лапшина

УДК 517 Методические указания: Использование математического

моделирования при решении прикладных задач для организации самостоятельной работы по курсу «Математика» для студентов специальности 230201 «Информационные системы и технологии» очной формы обучения. Ч. 1 / ФГБОУВПО «Воронежский государственный технический университет»; сост. В.В. Дежин, М.Л. Лапшина. Воронеж, 2011. 29 с.

Методические указания предназначены в качестве руководства для самостоятельного изучения студентами специальности 230201 (ИС) очной формы обучения раздела «Теория вероятностей и математическая статистика» курса «Математика». Методические указания включают в себя 3 занятия и содержат ссылки на литературу, пояснения и примеры, контрольные вопросы и задачи, форму отчетности.

Предназначены для студентов четвертого семестра второго курса.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word и содержатся в файле Веро- ятность-1.pdf.

Ил. 3. Библиогр.: 14 назв.

Рецензент канд. физ.-мат. наук, проф. Г.Е. Шунин

Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© ФГБОУВПО «Воронежский государственный технический университет», 2011

Занятие № 1

ПОНЯТИЕ СЛУЧАЙНОГО СОБЫТИЯ. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ НАД СОБЫТИЯМИ

1.1. Основные понятия

Предметом теории вероятностей являются модели экспе-

риментов со случайными исходами. При этом рассматриваются только такие эксперименты, которые можно повторять при неизменном комплексе условий произвольное число раз. Любой наблюдаемый результат эксперимента интерпретируется как случайный исход опыта (случайное событие). Математическая формализация модели случайного эксперимента включает в себя: 1) построение множества элементарных исходов , 2) описание поля событий для данного эксперимента, 3) задание вероятностного распределения на поле событий. Под мно-

жеством элементарных исходов понимают множество взаимоисключающих исходов такое, что результатом эксперимента всегда является один и только один исход. Любое подмножество данного множества интерпретируется как событие. Совокупность всех наблюдаемых событий составляет поле событий для данного эксперимента. Понятия, связанные с 2) и 3), определяются строго в аксиоматической теории вероятностей. Множество для данного эксперимента может быть дискретным, непрерывным или иметь более сложную структуру. К дискретным относятся конечные или счетные множества.

Говорят, что событие A произошло (наступило, осуще-

ствилось, реализовалось), если результатом эксперимента явился элементарный исход , принадлежащий A. Событие, совпадающее с пустым множеством , называется невозможным событием, а событие, совпадающее со всем множеством– достоверным событием. Два события A и B называются

совместными (несовместными), если в результате экспери-

мента возможно (невозможно) их совместное осуществление.

2

Другими словами, события A и B совместны, если соответствующие множества A и B имеют общие элементы, и несовместны в противном случае.

Поскольку событие отождествляется с множеством, то над событиями можно совершать все операции, выполнимые над множествами. В частности определены следующие операции и отношения между событиями:

A B (множество A является подмножеством множест-

ва B ) – событие A влечет за собой событие B .

A B (отношение эквивалентности множеств) – собы-

тие A тождественно событию B . Это возможно в том и только в том случае, когда A B и B A.

A B (объединение множеств) – сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий A или B .

AB (пересечение множеств) – произведение событий. Это событие, состоящее в совместном осуществлении событий A и B . События A и B несовместны, если AB .

A B (множество элементов, принадлежащих A, но не принадлежащих B ) – разность событий. Это событие, состоящее в том, что A происходит, а B не происходит.

A A (дополнение множества A до ) – противоположное событие. Это событие, состоящее в том, что A не происходит.

Операции сложения и умножения обладают свойствами

коммутативности, ассоциативности, дистрибутивности,

как арифметические операции над числами, но A A A,

AA A, A BC A B A C .

Справедливы также следующие тождества:

а) A A, A , A , A A.

б) A B AB , AB A B (правила де Моргана).

в) A B B A AB AB A B . Это равенство пока-

зывает, что приводить подобные в алгебре событий нельзя. 3

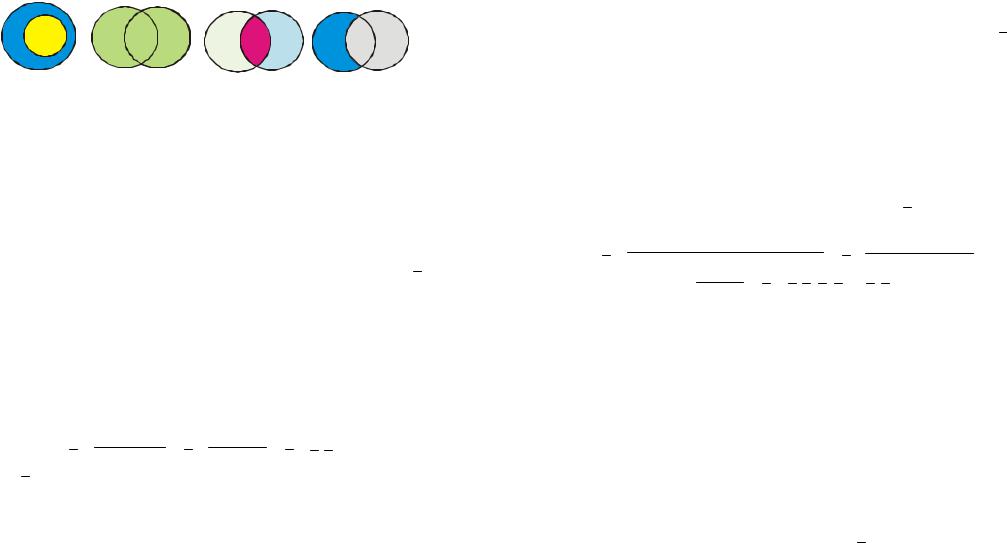
Для наглядного представления операций над событиями используются диаграммы Венна (рис. 1).

1.2. Примеры решения задач

Пример 1. Производственная установка состоит из двух энергетических устройств и одной машины. Рассматриваются события: A {исправна машина}, Bk {исправно k -е энерге-

тическое устройство}, C {работоспособность установки}. Установка работоспособно, если исправна машина и хотя бы

одно энергетическое устройство. Выразить события C и C через элементарные события A и Bk .

Решение. Событие B1 B2 означает наступление хотя бы одного из событий B1 и B2 , т.е. исправность первого энергетического устройства или второго устройства или исправность обоих устройств. Событие C означает одновременное наступ-

Получаем C A B1 B2 A B1 B2 A B1B2 , т.е. собы-

тие C означает неисправность машины и (или) обоих энергетических устройств.

Пример 2. Производственная установка состоит из управляющего устройства, четырех энергетических устройств и двух машин. A {исправно управляющее устройство},

4

производственной установки, что будет в том случае, когда исправны управляющее устройство, хотя бы одно энергетическая установка и хотя бы одна машина. Выразить события D и D через события A, Bk и Cj .

Решение. Исправности хотя бы одного энергетического устройства соответствует наступлении хотя бы одного из событий Bk , т.е. событие B1 B2 B3 B4 . Аналогично событие

C1 C2 соответствует исправности хотя бы одной машины. Событие D означает одновременное наступление событий A, B1 B2 B3 B4 и C1 C2, таким образом D A B1 B2

B3 B4 C1 C2 . Для определения события D воспользуем-

ся правилами де Моргана. Получаем

D A B1 B2 B3 B4 C1 C2 A B1 B2 B3 B4

C1 C2 A B1B2B3B4 C1C2 ,

что означает неисправность управляющего устройства или неисправность всех энергетических устройств или неисправность обоих машин.

Пример 3. Предприятие состоит из двух цехов, производящих изделия первого типа, и трех цехов, производящих изделия второго типа. Рассмотрим события: Ak {успешная ра-

бота k -го цеха, производящего изделия первого типа} и Bj {успешная работа j -го цеха, производящего изделия вто-

рого типа}. Предприятие сможет выполнить заказ при условии успешной работы хотя бы одного цеха, производящего изделия первого типа и успешной работы не менее двух цехов, производящих изделия второго типа. C {предприятие сможет выполнить заказ}. Выразить события C и C через элементарные события Ak и Bj .

5

Решение. Успешной работе хотя бы одного цеха, производящего изделия первого типа, соответствует событие A1 A2 . События: B1B2 {успешная работы цехов № 1 и № 2, производящих изделия второго типа}, B1B3 {успешная работы цехов № 1 и № 3, производящих изделия второго типа}, B2B3 {успешная работы цехов № 2 и № 3, производящих из-

делия второго типа}. Успешной работе не менее двух цехов, производящих изделия второго типа, соответствует событие

воспользуемся правилами де Моргана. Получаем

CA1 A2 B1B2 B1B3 B2B3 A1 A2

B1B2 B1B3 B2B3 A1A2 B1B2 B1B3 B2B3

A1A2 B1 B2 B1 B3 B2 B3

A1A2 B1 B2B3 B2 B3 A1A2 B1B2 B1B3 B2B3.

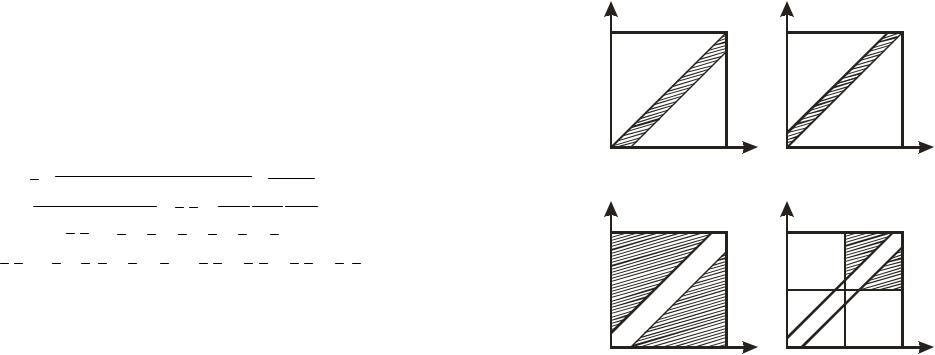
Пример 4. Два железнодорожных состава должны подойти под погрузку к одной и той же платформе. Время прихода обоих составов независимо и равновозможно в течение данных суток. Время погрузки первого состава 3 часа, а второго – 4 часа. Изобразить графически следующие событии: A {первому составу придется ожидать освобождения платформы}, B {второму составу придется ожидать освобождения платформы}, C {ни одному из составов не придется ожидать освобождения платформы}, D {время ожидания одним составом другого будет не больше одного часа, при этом составы прибывают во второй половине суток}.

Решение. В данной задаче множество элементарных исходов является непрерывным, так как время изменяется непрерывно. Пусть x – время прихода первого состава, y – вто-

6

рого состава. Рассмотрим систему координат с осями x и y . Так как 0 x 24 и 0 y 24, то областью возможных значе-

в) г) Рис. 2

В случае события A первый состав приходит позже второго, т.е. x y , но не позже окончания погрузки второго со-

лежит между прямыми y x и y x 4 (рис. 2, а).

В случае события B второй состав приходит позже первого, т.е. y x, но не позже окончания погрузки первого со-

7

става, т.е. y x 3. Получаем x y x 3. Данная область лежит между прямыми y x и y x 3 (рис. 2, б).

В случае события C первый состав может прибыть позже окончания погрузки второго состава, т.е. x y 4, или второй состав может прибыть позже окончания погрузки первого, т.е. y x 3. Данные области лежат ниже прямой y x 4 и выше прямой y x 3 (рис. 2, в).

В случае события D первый состав может прибыть за час до окончания погрузки второго или позже, т.е. x y 3, или второй состав может прибыть за час до окончания погрузки первого или позже, т.е. y x 2. Так как составы прибывают во второй половине суток, то x 12 и y 12. Области, удовлетворяющие этим условиям, изображены на рис. 2, г.

1.3.Контрольные вопросы и задания

1.Что является предметом теории вероятностей?

2.Что понимается под случайным событием?

3.Что называется множеством (пространством) элементарных исходов?

4.Что такое поле событий?

5.Каким может быть множество элементарных исходов?

6.Какие случайные события называются невозможными, достоверными, несовместными?

7.Когда одно событие является следствием другого?

8.Какие события называются равными, противополож-

ными?

9.Что называется суммой событий, произведением событий, разностью событий?

10.Приведите свойства алгебраических операций.

11.Запишите правила де Моргана и проиллюстрируйте их на диаграммах Венна.

12.Приведите примеры случайных событий в экономике.

8

1.4.Задачи для самостоятельной работы

1.Обобщите правила де Моргана на произвольное число событий.

2.Докажите тождества:

1) A B A B A, 2) A B A B A B AB, 3) A B A C A BC, 4) AC B AC BC, 5) A BC B AC C AB ABC ABC .

3. На производственном участке работают три станка. События A, B и C – выход из строя, соответственно, 1-го, 2- го и 3-го станка. Выразите через события A, B и C следующие события: D1 {один станок выйдет из строя}, D2 {два

из строя}, D8 {хотя бы два станка не выйдут из строя}.

4. Из ящика, содержащего 10 деталей, из которых 3 бракованных, наудачу последовательно и без возвращения извлекают по одной детали до появления бракованной, после чего опыт прекращается. Обозначим событие i {при i-м испы-

тании появится бракованная деталь}. Сконструируйте элементарные исходы данного опыта с помощью алгебраических операций над событиями i . Запишите событие A {придется

проводить третье по счету извлечение детали} через i и уп-

ростите запись путем алгебраических преобразований.

5. Два предпринимателя (назовем их Покупатель и Продавец) договорились о встрече в определенном месте между 14 и 15 часами. Каждый приходит в случайный момент указанного промежутка времени и ждет появления другого до 15 часов. При этом Покупатель ждет не более 10 минут, а Продавец – не

9

более 20 минут. Изобразите графически следующие события: A {встреча состоялась}, B {Продавец ждал Покупателя все обусловленное время и не дождался}, C {Покупателю не пришлось ждать Продавца}, D {встреча состоялась до 14.30}, E {Покупатель опоздал на встречу}, F {встреча состоялась, когда до истечения часа оставалось меньше 5 минут}.

Форма отчетности: устный опрос, типовой расчет, экза-

мен.

Занятие № 2 ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

2.1. Основные понятия

Решение вероятностных задач на классическую схему часто облегчается использованием комбинаторных формул. Каждая из комбинаторных формул определяет общее число элементарных исходов в некотором опыте, состоящем в выборе наудачу m элементов из n различных элементов исходного множества E e1, e2, , en . При этом в постановке каждого

такого опыта строго оговорено, каким способом производится выбор и что понимается под различными выборками.

Фундаментальные правила комбинаторики – правила сумм и произведений. Пусть множество A состоит из n элементов: A a1, a2, , an , а множество B – из m элементов:

B b1, b2, , bm .

Правило суммы. Если элемент a можно выбрать n способами ( т.е. любой ai из A), а элемент b – m способами, то выбор элемента «a или b » может быть осуществлен n m способами.

10

Правило произведения. Если элемент a можно выбрать n способами, а элемент b – m способами, то пару a, b можно

выбрать n m способами.

Существуют две различные схемы выбора. В первой схеме выбор осуществляется без возвращения элементов (это значит, что отбираются сразу все m элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества). Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента в исходное множество на каждом шаге и тщательным перемешиванием исходного множества перед следующим выбором. После того как выбор тем или иным способом осуществлен, отобранные элементы (или их номера) могут быть либо упорядочены (т.е. выложены в последовательную цепочку), либо нет. В результате получаются следующие четыре различные постановки эксперимента по выбору наудачу m элементов из общего числа n различных элементов множества E .

1. Схема выбора, приводящая к сочетаниям. Если опыт состоит в выборе m элементов без возвращения и без упорядочивания, то различными исходами следует считать m- элементные подмножества множества E , имеющие различный состав. Получаемые при этом комбинации элементов (элементарные исходы) носят название сочетания из n элементов по m, а их общее число определяется по формуле

Для чисел Cnm, называемых также биномиальными коэффици-

ентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач:

Cnm Cnn m (свойство симметрии),

11

ние),

Cn0 C1n Cnn 2n (следствие биномиальной формулы

Ньютона).

2. Схема выбора, приводящая к размещениям. Если опыт состоит в выборе m элементов без возвращения, но с упорядочиванием их по мере выбора в последовательную цепочку, то различными исходами данного опыта будут упорядоченные m-элементные подмножества множества E , отличающиеся либо набором элементов, либо порядком их следования. Получаемые при этом комбинации элементов (элементарные исхо-

ды) называются размещениями из n элементов по m, а их об-

щее число определяется по формуле

В частном случае m n опыт фактически состоит в произвольном упорядочивании множества E , т.е. сводится к случайной перестановке элементов всего множества. Получаемые при этом комбинации элементов (элементарные исходы) называются перестановками n элементов, а их общее число определяется по формуле N Pn n!.

Схема выбора, приводящая к сочетаниям с повторения-

ми. Если опыт состоит в выборе с возвращением m элементов множества E e1, e2, , en , но без последующего упорядо-

чивания, то различными исходами такого опыта будут всевозможные m-элементные наборы, отличающиеся составом. При этом отдельные наборы могут содержать повторяющиеся эле-

e2, e1, e1, e1 неразличимы для данного эксперимента, а набор

e1, e1, e3, e1 отличен от любого из предыдущих. Получаю-

12

щиеся в результате данного опыта комбинации называются сочетаниями с повторениями, а их общее число определяется формулой

Схема выбора, приводящая к размещениям с повторе-

ниями. Если выбор m элементов из множества E e1, e2, , en производится с возвращением и с упорядочиванием их в

последовательную цепочку, то различными исходами будут всевозможные m-элементные наборы (вообще говоря, с повторениями), отличающиеся либо составом элементов, либо

ными исходами данного опыта. Получаемые в результате ком-

бинации называются размещениями с повторениями, а их об-

2.2. Примеры решения задач

Пример 1. Множество E состоит из трех различных элементов: E a, b, c .Выписать состав множества всех ис-

ходов в пяти различных опытах: 1) произвольное упорядочивание элементов множества E ; 2) выбор двух элементов из множества E без возвращения и упорядочивания; 3) выбор двух элементов из множества E без возвращения с упорядочиванием; 4) выбор двух элементов из множества E с возвращением без упорядочивания; 5) выбор двух элементов из множества E с возвращением и с упорядочиванием.

Решение. 1) abc, acb, bac, bca, cab, cba , N 6.

В этом опыте выборки различаются только порядком элемен-

13

тов, т.е. опыт сводится к случайной перестановке элементов множества E , а число всех возможных перестановок равно

P3 3! 1 2 3 6 .

2) ab, ac, bc , N 3. В этом опыте выборки из

различных элементов различаются только составом, такие вы-

выборки из различных элементов различаются или составом или порядком элементов, такие выборки называются размеще-

выборки из элементов с повторением различаются только составом, такие выборки называются сочетаниями с повторения-

этом опыте выборки из элементов с повторением отличаются или составом или порядком, такие выборки называются раз-

мещениями с повторениями, поэтому N A32 32 9.

Пример 2. На завод поступают n различных изделий от первого поставщика и m различных изделий от второго поставщика. В день поступает одно изделие. Определить число способов распределения изделий по дням для произвольного порядка поступления и число способов распределения изделий по дням для следующих событий: A {изделия будут поступать поочередно от разных поставщиков}, B {сначала посту-

14

пят изделия от одного поставщика, а затем от другого}, C {все изделия от первого поставщика поступят подряд друг за другом}.

Решение. Всего имеется n m различных изделий, поэтому нахождение всех способов распределения изделий по дням сводится к нахождению числа различных перестановок n m элементов. Число таких перестановок равно Pn m

n m !. В случае события A необходимо учесть различный порядок поступления изделий от первого поставщика (число способов равно Pn n!), различный порядок поступления из-

делий от второго поставщика (число способов равно Pm m!),

а также два варианта чередования поступлений изделий от поставщиков: 121212 и 212121 (цифрой обозначен номер поставщика). В итоге число способов распределения изделий по дням для события A равно, согласно правилу произведения, N A 2 n! m!. В случае события B подсчет числа способов

такой же, только два варианта поступления изделий от поставщиков другие: 111 222 и 222 111 , поэтому N B 2n!m!. В случае события C также необходимо учесть различный порядок поступления изделий от первого поставщика (число способов равно Pn n!) и различный порядок поступления изделий от второго поставщика (число способов равно Pm m!). Варианты чередования поступления изделий от поставщиков следующие:

1 12 2, 21 12 2, 2 21 12 2 , 2 21 12, 2 21 1.

n m n m 1 k n m k m 1 n m n

Видно, что число таких вариантов равно m 1. Таким образом N C m 1 n!m! согласно правилу произведения.

Пример 3. n различных деталей случайным образом распределяются по m m n занумерованным ящикам таким

15

образом, чтобы k -й по счету ящик содержал ровно nk деталей

(n1 n2 nm n). Определить число способов распределе-

ния деталей по ящикам.

Решение. Представим данный эксперимент как последовательность испытаний, каждое из которых состоит в случайном заполнении очередного ящика. Вычислим число способов заполнения первого ящика N1. Опыт состоит в выборе n1 деталей без возвращения из n деталей, причем порядок расположения n1 деталей не важен. При такой схеме выбора число способов определяется числом сочетаний из n элементов по

логично получаем число способов заполнения остальных ящи-

ления деталей по ящикам определяем по правилу произведе-

сомножитель в знаменателе сокращается с числителем последующей дроби.

16

Пример 4. 8 акций первого предприятия, 6 акций второго предприятии и 7 акций третьего предприятия раскладываются в три пакета так, чтобы в каждом пакете было одинаковое число акций. Определить число всех способов распределения акций по пакетам и число способов распределения акций для следующих событий: A {в каждом пакете по две акции второго предприятия}, B {случайно выбранный пакет не содержит акции второго предприятия}.

Решение. Число всех способов распределения акций по пакетам определяется аналогично примеру 3, т.е. N

N1N2N3 C217 C147 C77 21!3 . В случае события A необходи-

7!

мо учесть, что общее число акций уменьшилось: 21-6=15 и в каждый пакет осталось положить 7-2=5 акций, поэтому

заполнении одного из пакетов производится случайный выбор 7 акций из 21-6=15, так как он не содержит акции второго предприятия, т.е. В остальные пакеты могут попасть любые

Пример 5. n человек приходят в магазин, в котором имеется m предметов (m n ), и покупают все предметы, причем каждый покупает не более одного предмета. Определить число всех способов распределения предметов между покупателями и число способов для следующих событий: A {l определенных лиц ничего не купят (l n m)}, B {k определенных лиц купят предметы (k m)}

Решение. Опыт состоит в выборе без возвращения m человек из n, которые купят m предметов, и распределении

17

предметов между ними (упорядочивание). Таким образом имеем размещения из n элементов по m, число всех способов распределения предметов между покупателями находится по

события B происходит выбор k предметов из имеющихся m и распределении их между k покупателями (упорядочивание),

соответствующее число способов равно Amk . Остальные n k

человек могут купить оставшиеся m k предметов, соответст-

Пример 6. На складе имеются детали 10 типов. Поступил заказ на 15 деталей. Считая, что число деталей каждого типа больше или равно 15, определить число всех возможных способов заказа.

Решение. Опыт состоит в выборе 15 элементов из 10 с повторением, но без упорядочивания. Поэтому число всех способов равно числу сочетаний с повторениями, т.е.

Пример 7. Изготовление 6 различных изделий может быть поручено 10 фирмам. Определить число способов размещения заказа для следующих событий: A {каждая фирма может получить заказ на изготовление любого числа изделий из имеющихся}, B {изготовление всех изделий будет поручено одной из фирм}, C {определенная фирма не получит заказ на изготовление изделий}, D {определенные 4 фирмы будут из-

18

готавливать по одному изделию}, E {одна из фирм будет изготавливать определенные 4 изделия}.

Решение. Рассмотрим событие A. Можно считать, что оно состоит в выборе фирмы изготовителя для каждого изделия, т.е. получается схема выбора 6 элементов из 10 с повторением (одной фирме может быть поручено изготовление нескольких изделий) и упорядочиванием (для изготовления каждого изделия может быть выбрана любая из фирм). Получаемые в результате комбинации являются размещениями с повторениями. Поэтому всех число способов размещения заказа

равно N A A106 106. Если рассуждать, что для каждого из-

делия есть 10 способов изготовления (10 фирм-изготовителей), то согласно правилу умножения придем к такому же результа-

ту: N A 10 10. В случае события B задача сводится к

6

выбору одной фирмы из 10, поэтому N B 10. Событие C

отличается от события A числом фирм, среди которых размещается заказ – вместо 10 фирм имеем 9, поэтому

N C A96 96 . В случае D предварительно определим число способов выбора 4 изделий, которые будут изготавливать 4

фирмы. Таких способов A64 , так как для изготовления каждого

изделия может быть выбрана любая из фирм. Оставшиеся 2 изделия будут распределены между остальными 6 фирмами,

число способов такого распределения равно A62 62. Общее число способов согласно правилу произведения будет равно

способов выбора фирмы, которая будет изготавливать 4 изделия, очевидно равно числу фирм, т.е. 10. Оставшиеся 2 изделия будут распределены между остальными 9 фирмами, число спо-

19