Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 283

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

360.06 Кб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

ФГБОУ ВО «Воронежский государственный технический университет»

Кафедра высшей математики и физико-математического моделирования

126-2017

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для организации самостоятельной работы по курсу «Высшая математика»

для студентов направления 20.01.03 «Техносферная безопасность»

(направленности «Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды»)

очной формы обучения

Воронеж 2017

Составитель канд. физ.-мат. наук И.Н. Пантелеев

УДК 517.2 (07) ББК 22.1я7

Элементы математической статистики: методические указания для организации самостоятельной работы по курсу «Высшая математика» для студентов направления20.01.03 «Техносферная безопасность» (направленности «Защита в чрезвычайных ситуациях», «Безопасность жизнедеятельности в техносфере», «Защита окружающей среды») очной формы обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост. И.Н. Пантелеев. Воронеж, 2017. 42 с.


	Методические		указания		предназначены		в	качестве
руководства		для	организации		самостоятельной		работы по
курсу "Высшая математика" по разделу «Теория вероятностей
и	матстатистика»		для	студентов		направления20.01.03
«Техносферная безопасность» в 4 семестре. В работе							приведен
теоретический		материал,		необходимый		для	выполнения
заданий и решение типовых примеров.
	Методические		указания		подготовлены в		электронном
виде и содержатся в файле Vmfmm_MatStat_17.pdf.

Табл.7. Ил. 2. Библиогр.: 8 назв.

Рецензент канд. физ.-мат. наук, проф. Г.Е. Шунин Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению учебно-методического совета Воронежского государственного технического университета

ÓФГБОУ ВО «Воронежский государственный

технический университет», 2017

1.Основные понятия математической статистики

1.1.Генеральная совокупность. Выборка. Основные типы задач математической статистики


Пусть		Х –	некоторая		случайная	величина
(количественный признак). В дальнейшем все значения этой
СВ	будем	называть		генеральной	совокупностью. Если,
например, Х – дискретная СВ, то генеральная совокупность –
х1 , х2 ,	…, хn.	что	в процессе наблюдений или			опытов мы
Допустим,

получили n значений (х1 , х2 , …, хn) случайной величины Х. В дальнейшем будем говорить, что сделали выборкух1 , х2 , …, хn из генеральной совокупности Х.

Число n называется объемом выборки.

Выборку х1 , х2 , …, хn из генеральной совокупности Х также можно представить, как значения n экземпляров х1 , х2 , …, хn случайной величины Х.

Заметим, что среди элементов выборки могут быть повторяющиеся. Поэтому для каждого элементахi выборки говорят о частоте ее появления, т.е. сколько раз числохi наблюдалось в выборке.

В дальнейшем мы часто будем задавать выборку в виде таблицы:

хi	х1	х2	…	хm
ni	n1	n2	…	nm

где х1 , х2 , …, хm – различные элементы выборки, а n1, n2, …, nm – частоты элементов выборки.

Ясно, что в этом случае объем выборки n = n1 + n2 +…+ nm

Значения х1 , … , хm выборки будем называть вариантами. Если варианты выборки расположены в возрастающем

порядке, то выборка называется вариационным рядом.

Например,

хi

-1

Варианты

выборки

называются равноотстоящими, если

Хi+1 - Xi = h, где h – постоянное число.

На практике при описании реальных процессов различные

характеристики процесса являются случайными величинами.

Поэтому

возникают

задачи

определения

зак

распределения,

математических

ожиданий

других

характеристик этих СВ, основываясь на изучении выборок.

Пусть

значения

СВХ

определяют

генеральную

совокупность

и F(x)=P(X

< x)

–

интегральная

функция

распределения

Х.

дальнейшем

мы

будем

ее

называть

теоретической

функцией

распределения

генеральной

совокупности Х. Зная

функцию F(x),

можно

определить

все

характеристики

СВ Х.

Поэтому

поставим

перед

собой

следующую задачу: можно ли с помощью выборок из гене-

ральной совокупности Х приближенно найти функцию F (x) ?

Пусть задана выборка объема n = n1 + n2 + … + nm.

хi

х1

х2

…

хm

…

Построим

функцию,

где nx – число

вариантов

выборки,

меньших х,

т.е.

представляет

относительную частоту

F *(x)

вариантов выборки, меньших х. Функция

называется

функцией

распределения

выборки

или

эмпирической

функцией распределения.

Пример 1. Найти эмпирическую функцию по выборке

хi	1	4	6
ni	10	15	25

Решение. Найдем объем выборки n = 10 + 15 + 25 = 50. Наименьшая варианта равна единице, следовательно, F *(x) = 0

при х ≤ 1. Значение Х < 4, а именно х1 = 1, наблюдалось 10 раз, следовательно,

F *(x) = 10 = 0, 2 при 1 < Х ≤ 4. 50

Значения Х < 6, а именно х1 = 1 и х2 = 4, наблюдались n1 + n2 = 10 + 15 = 25 раз, следовательно,


	F *(x) =	10		= 0, 2			при 4< Х ≤6.
		50

Так как х3 = 6 – наибольшая варианта, то
	F *(x) =		50		=1		при х > 6.

		50
	ì0	при				х £1
	ï	при				1 < х £ 4
Значит,	ï0, 2
	F *(x) = í	при				4< x £ 6,
	ï0,5
	ï	при				х > 6
	î1

Графически эта функция изображена на рис.1. 3

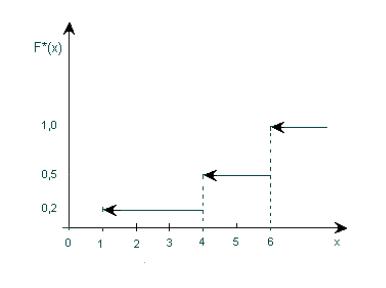
Рис.1

Эмпирическая функция F *(x) является приближением теоретической функции F (x) , и чем больше объем выборки n, тем точнее F *(x) описывает F (x) (по вероятности, т.е. случайные отклонения маловероятны).

1.2. Статистическая оценка параметров распределения

Пусть	значения	случайной	величиныХ	образуют
генеральную	совокупность. Закон		распределения		СВ
(например,	нормальный	закон) Х нам известен. Однако
неизвестны	некоторые	параметры	этого	распределения
(например, МО или дисперсия).
Требуется, изучая выборки из генеральной совокупности,
оценить, т.е. приближенно найти, неизвестный параметр.
Статистической		оценкой	неизвестного		параметра

называется всякая функция j варианта хi выборки, дающая приближенное значение этого параметра.

Если обозначим неизвестный параметр черезq , а его


оценку через q * , то q* = q (х1,…хn),				где	x1, … , xn – выборка
из генеральной совокупности Х.
Рассматривая варианты x1, … , xn выборки как значения n
экземпляров Х1, …, Хn		СВ Х, получим:q* = j (Х1, …, Хn), т.е.
статистическая оценка q *			является	функцией от		случайных
величин	Х1, …, Хn,, а	значит и		сама	является	. СВТаким
образом	статистическая		оценкаq *		принимает	значения

(различные) в зависимости от выборки.

Ясно, что для одного и того же неизвестного параметра можно построить различные статистические оценки. Наша

задача понять, какие оценки являются «хорошими».

Во-первых, естественно

желание, чтобы

статистическая

оценка,

являясь

случайной

величиной, имела

своим

математическим ожиданием неизвестный параметр.

Статистическая

оценка q *

неизвестного

параметра

называется несмещенной, если M(q*) =q .

Во-вторых, естественно

требовать, чтобы

значения

статистической

оценки q *

неизвестного

параметраq ,

которая

называется

эффективной, если

она

обладает

наименьшей дисперсией среди всех статистических оценок

параметра

q .

В-третьих, естественно

считать, что,

чем

больше объем

выборки,

тем

точнее

значение

статистической

оценки

определяет неизвестный параметр.

Статистическая

оценка q *

неизвестного

параметра

называется состоятельной, если она стремится по вероятности

к q , т.е.

limn®¥ P {

q * -q

< e

}=1 при любом e > 0 .

1.3. Генеральная средняя. Выборочная средняя

Пусть

значения

случайной

величиныХ

образуют

генеральную

совокупность.

Математическое ожидание Х

будем называть генеральной

средней

обозначать

т.е.

= M ( X ) .

xГ

Рассмотрим некоторую выборку х1 , х2 ,

…, хn (варианты

могут повторяться) из генеральной совокупности Х. Будем ее

рассматривать как значения n экземпляров Х1, Х2 …, Хn СВ Х.

Рассмотрим

статистическую

оценку

X 1 + X 2 + ... + Xn

которая

называется

выборочной

средней. Конкретное

значение статистической оценки

при выборке х1 , х2 ,

…,

хn

будет:

x1 + x2 +... + xn

Статистическая

оценка

является СВ,

конкретное

значение

зависящее от

выборки.

В дальнейшем и

будем называть выборочной средней.

Если выборка задана в виде таблицы

хi

х1

х2

…

хm

…

то ясно, что n = n1 + n2 + … + nm ,

x1 ×n1 + x2 ×n2 +... + xm ×nm

åxi ×ni

xB =

i=1

Выборочная

средняя XB

является

эффективной,

несмещенной и состоятельной статистической оценкой для математического ожидания M ( X ) , т.е. для генеральной

средней X G .

	1.4. Выборочная дисперсия
Пусть	значения	СВХ	образуют	генеральную
совокупность. Дисперсию D(X)			CB X будем	называть
генеральной	дисперсией	и	обозначатьDG , а	среднее
квадратическое отклонение		s G =	DG .

Требуется найти статистическую оценку для DG .

Пусть х1, х2, …, хn – выборка из генеральной совокупности Х, а Х1, Х2 …, Хn – n экземпляров Х. Рассмотрим статистическую оценку

DB =

å( Xi - X

B )2 ,

i=1

которая

называется

выборочной

дисперсией. DB -случайная

ве-личина. Ее

конкретное

значение

при

данной

выборкех1 ,

…, хn

равно

dB =

å(xi -

( dB

также

называется

n i =1

выборочной дисперсией).

Если выборка из генеральной совокупности задана в виде таблицы

хi	х1		х2			…	хm
ni	n1		n2			…	nm
n = n1 + n2 + … + nm , то
	1		n
			å(xi -		)2ni
				xB
	dB =	n		xB
		n	i=1			.
			n			.
			n

Пример 2. Пусть выборка задана таблицей

хi

-1

n = 5+3+1+1=10. Тогда

å xi×ni

+ (-1)

×3 +1×1+ 2 ×1

x =

i=1

0 ×5

= 0 ;

dB =

02 ×5 + (-1) ×32 +12 ×1+ 22 ×1

3 +1 + 4

= 0,8 .

является смещенной

статистической

оценкой

для

D(X). Поэтому

рассматривают

статистическую

оценку

s2 =

× DB ,

которая называется исправленной выборочной

n -1

дисперсией.

является

несмещенной

статистической

оценкой

для DG .

Нетрудно

видеть, что

при

большихn :

s2 » DB .

Величина

dB = s B

называется

выборочным

среднеквадратическим

отклонением, а

s2 = s =

n -1

s B

исправленным

выборочным

среднеквадратически

отклонением.

Пример 3. Пусть генеральная совокупность X подчинена

нормальному закону. Требуется оценить ее параметры.

Так

как

параметрами

нормального

распределения

являются

s = sG

a = M ( X ) =

, то

s » s

при объеме выборки n £ 30 ,

s » s B

при объеме выборки n > 30 .

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022358.32 Кб4Учебное пособие 279.pdf
#
30.04.2022222.57 Кб2Учебное пособие 28.pdf
#
30.04.2022358.52 Кб2Учебное пособие 280.pdf
#
30.04.2022358.61 Кб3Учебное пособие 281.pdf
#
30.04.2022359.13 Кб5Учебное пособие 282.pdf
#
30.04.2022360.06 Кб6Учебное пособие 283.pdf
#
30.04.2022360.37 Кб4Учебное пособие 284.pdf
#
30.04.2022360.75 Кб6Учебное пособие 285.pdf
#
30.04.2022361.04 Кб9Учебное пособие 286.pdf
#
30.04.2022362.92 Кб5Учебное пособие 287.pdf
#
30.04.2022363.09 Кб3Учебное пособие 288.pdf