
Методические указания. Сборник индивидуальных заданий по разделу «Интегральное исчисление функций одной действительной переменной» дисциплины «Математический анализ». Провоторова Е.Н
.pdfФГБОУ ВО «Воронежский государственный технический университет»
Кафедра «Высшая математика и физико-математическое моделирование»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Сборник индивидуальных заданий по разделу «Интегральное исчисление функций одной действительной переменной дисциплины «Математический анализ»
для студентов специальности 090301.65 «Компьютерная безопасность» и 090302.65 «Информационная безопасность телекоммуникационных систем»
очной формы обучения
Воронеж 2016
Составитель: канд. физ.-мат. наук Е.Н. Провоторова УДК 517.9
Методические указания: Сборник индивидуальных заданий по разделу «Интегральное исчисление функций одной действительной переменной» дисциплины «Математический анализ» для студентов специальностей 090301.65 «Компьютерная безопасность» 090302.65 и «Информационная безопасность телекоммуникационных систем» очной формы обучения / ФГБОУ ВО «Воронежский государственный технический университет»; сост.: Е.Н. Провоторова.
Воронеж, 2016. 56 с.
Методические указания представляют собой сборник домашних индивидуальных заданий по разделу «Интегральное исчисление функций одной действительной переменной» дисциплины «Математический анализ», изучаемому во втором семестре. Методические указания составлены в соответствии с учебными планами специальностей 090301.65 «Компьютерная безопасность» и 090302.65 «Информационная безопасность телекоммуникационных систем».
Издание подготовлено в электронном виде и содержится в файле int.PDF.
Рецензент канд. физ.-мат. наук, доц. А.Н. Шелковой
Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ФГБОУ ВО «Воронежский государственный технический университет», 2016
1. Введение
Эффективная организация изучения дисциплины «Математический анализ» основанная на правильном сочетании аудиторных учебных занятий, продуктивной самостоятельной работе студентов и систематическом контроле, играет основополагающую роль в глубоком математическом образовании современного студента. Исходя из этих принципов, рекомендуются следующие индивидуальные задания, обеспечивающие систематическую работу студентов и ее контроль в течение семестра и, в совокупности, охватывающие почти весь материал раздела « Интегральное исчисление функций одной действительной переменной» дисциплины «Математический анализ».
Наряду с традиционными текущими заданиями, студенты в течение каждого семестра выполняют индивидуальные домашние задания. Задания содержат теоретические вопросы, теоретические упражнения, расчетную часть – типовые задачи и задачи прикладного характера.
Теоретические вопросы и теоретические упражнения являются общими для студентов, задачи – для каждого студента группы индивидуальные. Номер варианта, выполняемого студентом, соответствует его порядковому номеру в списке группы и сообщается преподавателем студенту.
Теоретические упражнения и расчетные задания выполняются в отдельной тетради и проверяются преподавателем. Завершающим этапом является защита ИДЗ . Во время защиты студент должен уметь правильно ответить на теоретические вопросы, пояснить решения теоретических упражнений и задач, решить задачи аналогичного типа.
2.Теоретические вопросы
1. Понятие первообразной функции. Теоремы о пер-
вообразных.
2.Неопределенный интеграл, его свойства.
3.Таблица неопределенных интегралов.
4.Замена переменной и интегрирование по частям в неопределенном интеграле.
5.Разложение дробной рациональной функции на простейшие дроби.
6.Интегрирование простейших дробей. Интегрирова-
ние рациональных функций.
7 Интегрирование выражений, содержащих тригоно-
метрические функции.
8.Интегрирование иррациональных выражений.
9.Понятие определенного интеграла, его геометриче-
ский смысл.
10.Основные свойства определенного интеграла.
11.Теорема о среднем.
12.Производная определенного интеграла по верхнему пределу. Формула Ньютона – Лейбница.
13.Замена переменной и интегрирование по частям в определенном интеграле.
14.Интегрирование биномиальных дифференциалов.
15.Вычисление площадей плоских фигур.
2

16. Определение и вычисление длины кривой, диффе-
ренциал длины дуги кривой.
3.Теоретические упражнения
1. Доказать, что для любой нечетной функции f x
справедливо равенство
0 a
f x dx f x dx
a 0
2. Какой из интегралов больше:
|
1 |
sin x 2 |
|
1 |
sinx |
|||
|
0 |
|
|
|
dx или |
0 |
|
dx? |
|
|
|
||||||
|
|
x |
|
|
x |
|||
|
3. Пусть |
|
f t |
– |
непрерывная функция, а функции |
|||
x |
и x |
дифференцируемые. Доказать, что |
||||||
x2
4. Найти d et2 dt.
dx 
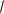 x
x
5. Найти точки экстремума функции
x
f x t 1 t 2 e t2 dt.
0
3
6. Пусть f x – непрерывная периодическая функ-
ция с периодом T. Доказать, что
a T T
|
|
f x dx f x dx |
a. |
|
|||||||||||
|
|
a |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Доказать, что если f x |
– четная функция, то |
|||||||||||||
|
0 |
a |
|
|
|
1 |
a |
|
|
|
|
||||
|
f x dx |
f x dx |
f x dx. |
|
|||||||||||
|
|
|
|
|
|||||||||||
|
a |
0 |
|
|
|
2 |
a |
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
2 x |
|
|
|||
|
8.Чему равен интеграл sin2 xln |
dx? |
|
||||||||||||
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
2 x |
|
||||
|
9. При каком условии, связывающем коэффициенты |
||||||||||||||
|
|
интеграл |
|
ax2 bx c |
|
|
|
|
|
|
|||||
a, b, c |
|
|
|
|
dx |
является |
рацио- |
||||||||
|
x3 x 1 2 |
||||||||||||||
нальной функцией? |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
10. |
При каких |
целых |
значениях |
n интеграл |
||||||||||
|
|
|
|
|
|||||||||||
1 x4 dx выражается элементарными функциями. |
|||||||||||||||
|
11. Считая, что функция |
sinx |
|
равна 1 при |
x 0, |
||||||||||
|
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
доказать, что она интегрируема на отрезке 0, |
|
1 . |
|
||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
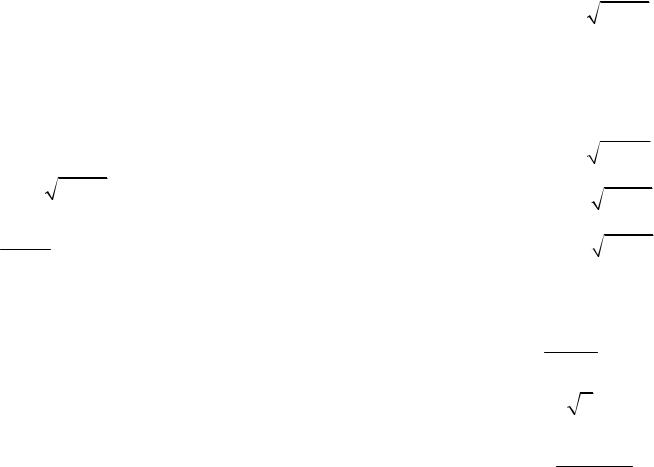
12. Доказать, что для любой нечетной функции
a
f x справедливо равенство |
|
f x dx 0. |
|
a |
|
4. Основные методы интегрирования
Задача 1. Найти неопределенные интегралы.
1.1.xsin2 xdx.
1.2.arctg
 9x 1dx.
9x 1dx.
1.3.sinxdx2 x.
1.4.6x 2 cos2xdx.
1.5.2 18x sin4xdx.
1.6.3x 2 e2xdx.
1.7.1 6x e2xdx.
1.8.ln x2 4 dx.
1.9.ln 4x2 1 dx.
5
1.102 4x sin2xdx.
1.11.arctg
 6x 1dx.
6x 1dx.
1.12.e 5x 4x 3 dx.
1.13.e 3x 2 9x dx.
1.14.arctg
 2x 1dx.
2x 1dx.
1.15.arctg
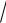 3x 1dx.
3x 1dx.
1.16.arctg
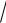 5x 1dx.
5x 1dx.
1.17.5x 6 cos2xdx.
1.18 cosxdx2 x.
1.19.x
 2 3 cos2xdx.
2 3 cos2xdx.
xcosxdx
1.20.sin3 x .
6

Задача 2. Вычислить определенные интегралы.
0x
2.1.x2 2 e2 dx.
2
0
2.2. 3x2 4 cos5xdx.
2
0
2.3. x2 4x 3 cosxdx.
1
0
2.4. x 2 2 cos3xdx.
2
0
2.5. x2 7x 12 cosxdx.
4
2.6. 2x2 4x 7 cos2xdx.
0
2.7. 9x2 9x 11 cos3xdx.
0
2.8. 8x2 16x 17 cos4xdx.
0
2
2.9. 3x2 5 cos2xdx.
0
2
2.10. 2x2 15 cos3xdx.
0
2
2.11. 3 7x2 cos2xdx.
0
2
2.12. 1 8x2 cos4xdx.
0
0
2.13. x2 2x 1 sin3xdx.
1
3
2.14. x2 3x sin2xdx.
0
2.15. x2 3x 2 sinxdx.
0
2
2.16. x2 5x 6 sin3xdx.
0
7 |
8 |

0
2.17. x2 6x 9 sin2xdx.
3
4
2.18. x2 17,5 sin2xdx.
0
2
2.19. 1 5x2 sin xdx.
0
1x
2.20.x2 e 2 dx.
1
Задача 3. Найти неопределенные интегралы.
5x3
3.1. x2 3dx.
3.2. 1 4lnx xdx.
3.3. x  5dxx2 1.
5dxx2 1.
3.4. x2 lnx2 dx.
3x
3.5. |
|
|
|
xdx |
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
x |
4 |
x |
2 |
1 |
||||||||
|
|
|
|
|
|
|
||||||
3.6. |
|
arccosx 3 1 |
||||||||||
|
|
|
|
|
|
|
|
|
dx. |
|||
|
|
|
|
|
|
|
|
|
||||
|
1 x |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
3.7. tgxlncosxdx.
x 1
3.8.cos2 x 1 dx.tg
x3
3.9.dx.
x2 1 2
1cosx
3.10.(x sinx)2 dx.
3.11. |
|
sinx cosx |
|||||
|
|
|
dx. |
||||
(cosx sinx)5 |
|||||||
3.12. |
xcosx sinx |
||||||
|
|
|
|
dx. |
|||
|
|
xsinx 2 |
|||||
|
x |
3 |
|
|
|
||
3.13. |
|
x |
dx. |
||||
|
|
4 |
|||||
|
|
x |
1 |
||||
9 |
10 |
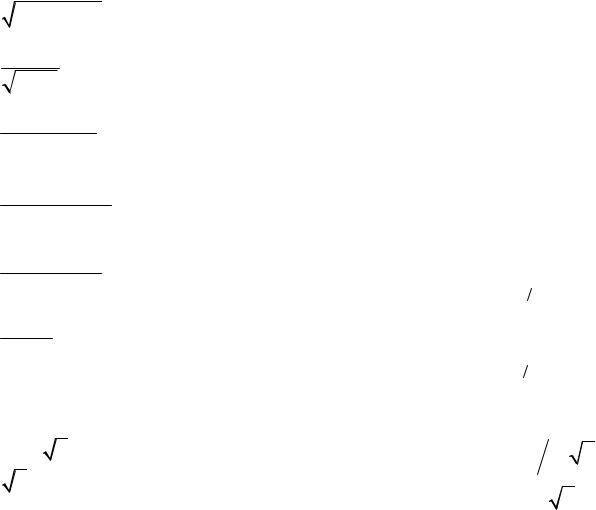
3.14. |
|
|
|
xdx |
|
|
. |
|
|
|
|
|
|
|
|
||
x |
4 |
x |
2 |
|
||||
|
|
|
|
1 |
||||
7xdx
3.15.3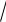 x 5.
x 5.
3.16.1 ln(x 1)dx.
x1
x2 1 dx
3.17.(x3 3x 1)5 .
3.18.4arctgx xdx.
1x2
x3
3.19.2 4dx.x
3.20. |
|
x cosx |
|
dx. |
|||||
x |
2 |
|
|
|
|
|
|||
|
|
|
2sinx |
||||||
|
|
1 |
|
|
|
||||
3.31. |
|
x |
dx. |
||||||
|
|
|
|
|
|
|
|||
|
|
x x 1 |
|||||||
|
|
|
|
|
|||||
Задача 4. Вычислить определенные интегралы.
 4
4
4.1.tgxlncosxdx.
0
|
1 |
|
|
|
2 x2 1 dx |
|
||||||||||||||
4.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||
x3 |
3x 1 |
2 |
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|||||||||||||
|
1 |
|
5arctgx 3x |
|
||||||||||||||||
4.3. 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx. |
|
||||
|
|
|
|
1 x2 |
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
x3dx |
|
|
|
|
|
|
|
|
|||||||
4.4. 0 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
x2 4 |
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
x cosx |
|
|
|
|
|
|
|
||||||||
4.5. |
|
|
|
|
|
|
|
|
|
dx. |
|
|||||||||
|
|
x2 2sinx |
|
|||||||||||||||||
|
4 |
|
2cosx 3sin x |
|
||||||||||||||||
4.6. |
0 |
|
|
|
|
|
|
|
|
|
dx. |
|||||||||
|
2sinx 3cosx 3 |
|||||||||||||||||||
|
1 2 8x arctg2x |
|
||||||||||||||||||
4.7. |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx. |
|
|||
|
|
|
|
1 4x2 |
|
|
|
|
|
|
||||||||||
|
4 1 2 |
|
1 |
|
|
|
|
|
||||||||||||
|
x |
|
|
|
|
|
||||||||||||||
4.8. |
|
|
|
|
|
|
|
|
|
|
|
|
dx. |
|
||||||
|
|
|
|
x |
2 |
|
|
|||||||||||||
|
1 |
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
xdx |
|
|
|
|
|
|
|
|
||||||
4.9. 0 |
|
. |
|
|
|
|
|
|
|
|
||||||||||
x4 1 |
|
|
|
|
|
|
|
|
||||||||||||
11 |
12 |
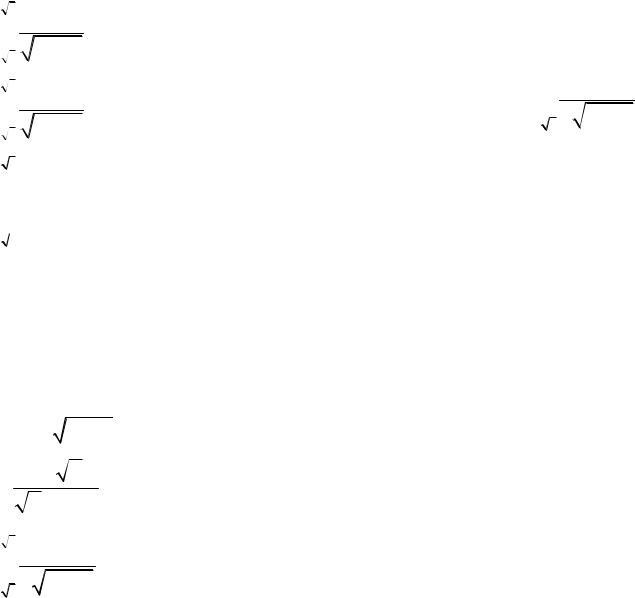

 8 x 1
8 x 1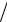 xdx.
xdx.

 3
3 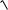 x2 1
x2 1

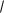 8 x 1
8 x 1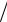 xdx.
xdx.

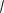 3
3  x2 1
x2 1
|
3 arctgx x |
|
|
|
||||||||
4.12. 0 |
|
|
|
|
|
|
dx. |
|||||
|
|
1 x2 |
|
|||||||||
|
|
|
x arctgx 4 |
|||||||||
|
3 |
|||||||||||
4.13. 0 |
|
|
|
|
|
|
|
|
dx. |
|||
|
|
1 x2 |
|
|
|
|||||||
1 |
|
|
|
|
x3 |
|
|
|
|
|
||
4.14. 0 |
|
|
|
dx. |
|
|
|
|
|
|||
|
x2 1 |
|
|
|
|
|
||||||
sin1 arcsinx 2 |
1 |
|||||||||||
4.15. |
|
|
|
|
|
|
|
|
dx. |
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 x |
2 |
|
|||||||
0 |
|
|
|
|
|
|
|
|
||||
31 
 x
x
4.16.1 
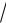 x x 1 dx.
x x 1 dx.

 8 dx
8 dx
4.17.x x2 1.3
e |
1 lnx |
|
|
4.18. |
dx. |
||
|
|||
1 |
x |
||
2dx
4.19.2 x 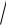 x2 1.
x2 1.
e |
2 |
lnx |
2 |
|
|
4.20. |
x |
|
|
dx. |
|
|
|
x |
|
||
1 |
|
|
|
|
|
Задача 5. Найти неопределенные интегралы.
5.1. |
|
2x3 40x 8 |
dx. |
||||||||
|
|
|
|
|
|
||||||
|
|
|
x(x 4)(x 2) |
||||||||
5.2. |
|
5x3 1 |
|||||||||
|
|
|
|
|
|
dx. |
|||||
|
|
x |
2 |
|
|||||||
|
|
|
|
1 |
|||||||
5.3. |
|
|
x3 7 |
dx. |
|||||||
x |
2 |
|
|||||||||
|
|
|
|
4x 3 |
|||||||
5.4. |
|
|
2x3 5 |
||||||||
|
|
|
|
|
dx. |
||||||
x |
2 |
|
|
||||||||
|
|
|
|
x 2 |
|||||||
5.5. |
|
|
2x3 1 |
||||||||
|
|
|
|
|
dx. |
||||||
x |
2 |
|
|
||||||||
|
|
|
|
x 6 |
|||||||
5.6. |
|
|
3x3 25 |
||||||||
|
|
|
|
|
|
|
|
dx. |
|||
|
x |
2 |
|
|
|
|
|||||
|
|
|
|
3x 2 |
|||||||
13 |
14 |

x3 2x2 3
5.7. x 1 x 2 x 3 dx.
3x3 2x2 1
5.8. x 2 x 2 x 1 dx.
x3
5.9. x 1 x 1 x 2 dx.
x3 3x2 12
5.10. x 4 x 3 x 2 dx.
x3 3x2 12
5.11. x 4 x 3 x dx.
5.12. x x 1 x 2 dx.
3x3 2
5.13. x3 x dx.
x3 3x2 12
5.14. x 4 x 2 x dx.
5.15. x5 x3 1dx.
5.16. |
x5 |
3x3 1 |
|||
|
|
|
|
dx. |
|
|
x |
2 |
|
||
|
|
|
x |
||
5.17. |
2x5 |
|
8x3 3 |
||||||||
|
|
|
|
dx. |
|||||||
x |
2 |
|
|||||||||
|
|
|
|
|
2x |
||||||
5.18. |
|
3x5 |
12x3 7 |
||||||||
|
|
|
|
|
|
|
|
|
dx. |
||
|
x |
2 |
|
|
|
||||||
|
|
|
2x |
||||||||
5.19. |
|
x5 |
|
9x3 4 |
|||||||
|
|
|
|
|
|
|
dx. |
||||
|
x |
2 |
|
|
|||||||
|
|
|
|
3x |
|||||||
5.20. |
|
x5 |
|
25x3 1 |
|||||||
|
|
|
|
|
|
|
|
|
|
dx. |
|
|
|
x |
2 |
|
|
|
|
||||
|
|
|
|
5x |
|||||||
Задача 6. Найти неопределенные интегралы.
6.1. |
x3 6x2 13x 9 |
dx. |
|||
(x 1)(x 2)3 |
|||||
6.2. |
x3 6x2 13x 8 |
dx. |
|||
x(x 2)3 |
|
|
|||
6.3. |
x3 6x2 13x 6 |
dx. |
|||
(x 2)(x 2)3 |
|
||||
6.4. |
x3 6x2 14x 10 |
||||
|
|
dx. |
|||
(x 1)(x 2)3 |
|
||||
15 |
16 |

6.5. |
x3 |
6x2 11x 10 |
|||||||||
|
|
|
|
|
|
|
|
|
dx. |
||
|
|
|
(x 2)(x 2)3 |
|
|
||||||
6.6. |
x3 6x2 11x 7 |
dx. |
|||||||||
|
|
(x 1)(x 2)3 |
|
|
|||||||
6.7. |
2x3 6x2 7x 1 |
dx. |
|||||||||
|
|
|
(x 1)(x 1)3 |
|
|||||||
6.8. |
x3 |
6x2 10x 10 |
|||||||||
|
|
|
|
|
|
|
dx. |
||||
|
|
|
(x 1)(x 2)3 |
|
|
|
|||||
6.9. |
2x3 6x2 7x 2 |
||||||||||
|
|
|
|
|
|
dx. |
|||||
|
|
|
x(x 1)3 |
|
|||||||
6.10. |
|
x3 6x2 13x 8 |
|||||||||
|
|
|
|
|
|
dx. |
|||||
|
|
x(x 2)3 |
|
|
|||||||
6.11. |
|
x3 6x2 13x 7 |
|||||||||
|
|
|
|
|
|
dx. |
|||||
|
|
(x 1)(x 2)3 |
|
|
|
||||||
6.12. |
|
x3 6x2 14x 6 |
|||||||||
|
|
|
|
|
|
dx. |
|||||
|
|
(x 1)(x 2)3 |
|
|
|
||||||
6.13. |
x3 6x2 10x 10 |
||||||||||
|
|
|
|
|
|
dx. |
|||||
|
(x 1)(x 2)3 |
|
|
|
|
||||||
6.14. |
x3 x 2 |
|
|
|
|
|
|||
|
dx. |
|
|
|
|
|
|||
x 2 x3 |
|
|
|
|
|
||||
6.15. |
3x3 9x2 10x 2 |
||||||||
|
|
|
|
|
dx. |
||||
(x 1)(x 1)3 |
|
||||||||
6.16. |
2x3 x 1 |
|
|
|
|
|
|||
|
dx. |
|
|
|
|
|
|||
x 1 x3 |
|
|
|
|
|
||||
6.17. |
2x3 6x2 7x 4 |
dx. |
|||||||
(x 2)(x 1)3 |
|||||||||
6.18. |
|
2x3 6x2 5x |
|
dx. |
|
|
|||
|
(x 2)(x 1)3 |
|
|
|
|||||
6.19. |
|
2x3 6x2 7x |
|
dx. |
|
|
|||
|
(x 2)(x 1)3 |
|
|
|
|||||
6.20. |
2x3 6x2 5x 4 |
dx. |
|||||||
(x 2)(x 1)3 |
|
||||||||
Задача 7. Найти неопределенные интегралы.
2x3 3x2 3x 2
7.1. x2 x 1 x2 1 dx.
17 |
18 |
