
Методы решения оптимизационных задач в медицине. Коровин В.Н
.pdf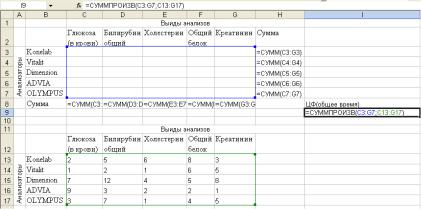
1,если_i_анализатор_выполняет_анализ x 0,если_иначе
Таким образом, в итоге нам необходимо определить, какой вид анализа будет выполнять каждый из анализаторов, чтобы суммарное время всех анализов было минимальным. Количество ограничений равно сумме количества анализов и количества анализаторов. В нашем случае число ограничений равно десяти.
В рабочем листе MS Excel создадим две таблицы (матрицы) с пятью столбцами и строками. Нижнюю (С13:G17) заполним исходными данными о времени выполнения анализов (рис. 16). Верхнюю матрицу (С3:G7) не будем заполнять, для нее лишь посчитаем суммы по строкам и столбцам, которые вначале примут значения нулей (ячейки С9:Н9 и I3:I9), а при нахождении опорного плана они обязательно должны быть равны единице, так как каждый вид анализа должен выполняться только один раз и каждый из анализаторов должен выполнять только один из видов анализа.
Рис. 16. Исходные данные задачи о назначениях
30
В ячейке I9 будем считать значение целевой функции — общее время проведения всех анализов. Ее значение представляет собой сумму произведений двух матриц: матрицы распределения анализаторов по видам анализов (С3:G7) и матрицы времени выполнения анализов (С13:G17). Дальнейшая работа выполняется в диалоговом окне «Поиск решения» (рис.17).
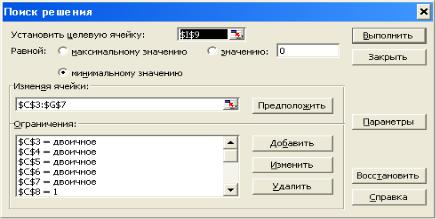
Рис. 17. Диалоговое окно «Поиск решения»
В этом окне устанавливаются целевая ячейка (I9), изменяемые ячейки (C3:G7), указывается направление поиска (минимизация). Далее вводятся ограничения: C3 = двоичное,
..G7 = двоичное (таких ограничений будет 25 по числу ячеек изменяемой матрицы), C8=1, D8=1, E8=1, F8=1, G8=1, H3=1, H4=1, H5=1, H6=1, H7=1 (таких ограничений будет 10 —
сумма строк и столбцов). Ограничение двоичных переменных позволяет ограничить переменную либо нулем (данная работа не выполняется конкретным сотрудником), либо единицей (работа выполняется). Ограничения на значения сумм столбцов и строк позволяет соблюсти условия того, что каждый из сотрудников может выполнять только один вид работ и каждая работа будет выполнена только одним сотрудником. В нашем случае мы используем линейную модель. Результаты оптимизации представлены на рис. 18.
31
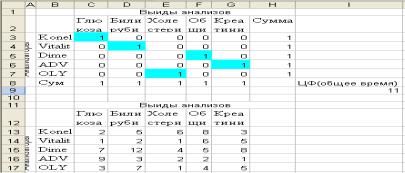
Рис. 18. Результаты оптимизации
Выделенные ячейки соответствуют распределению видов анализов между анализаторами. Значение целевой функции, равное 11, — минимальное значение времени выполнения всех анализов.
КОНТРОЛЬНЫЕ ВОПРОСЫ К ГЛАВЕ 3
1.В чем заключается задача о назначениях?
2.Какие исходные данные необходимы для решения такой задачи?
3.Почему целевая функция может стремиться и к минимуму, и к максимуму? От чего это зависит?
4.Сколько ограничений необходимо задать?
5.Как определяется целевая функция?
6. Какие дополнительные ограничения можно задать
ктакой задаче?
7.Что такое квадратичная задача о назначениях?
32
ГЛАВА 4. ТРАНСПОРТНАЯ ЗАДАЧА
Под транспортными задачами объединяется широкий круг задач с единой математической моделью. Такие задачи относятся к задачам линейного программирования и могут быть решены известным симплексным методом. Однако обычная транспортная задача имеет большое число переменных и решение ее симплексным методом очень громоздко. С другой стороны, матрица системы ограничений транспортной задачи весьма своеобразна, поэтому для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить последовательность опорных решений, которая завершается оптимальным решением.
Например, у нас есть сеть поставщиков лекарств, где хранятся медикаменты. Также имеется сеть аптек, которым требуется определенное количество лекарств. При этом на каждом складе поставщика различный объем запасов этих товаров. Кроме того, так как расстояние между различными аптеками и складами разное, то и отличается стоимость перевозок с определенного склада в определенную аптеку. Поэтому отличаются и тарифы − затраты на перевозку 1 товара от каждого склада к каждой аптеке. Возникает необходимость разработать такой план перевозок, чтобы аптеки получили требуемое количество медикаментов с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.
Для решения транспортной задачи необходимо знать количество товара на каждом из складов и потребность каждой аптеки (магазина) в этом товаре. Плюс следует знать все тарифы. Если тарифов нет, то можно с помощью различных интернет-сервисов определить соответствующие расстояния между поставщиками и потребителями и по среднему расходу топлива определить затраты (тарифы).
33
Есть у транспортной задачи и свои недостатки. Подразумевается, что перевозить мы будем только один вид товара, что бывает крайне редко. Плюс к этому, общая стоимость перевозок определяется как произведение тарифов на количество перевезенного товара. Таким образом, общая стоимость зависит от количества, а товар вполне может быть и малогабаритным. В этом случае если мы везем две, три или даже пятьдесят небольших коробок, то стоимость перевозки не должна отличаться. Поэтому транспортную задачу целесообразно использовать в следующих случаях:
–мы имеем несколько поставщиков и несколько потреби-
телей;
–перевозится только один вид груза;
–мы развозим крупногабаритный товар, только одна единица которого (контейнер, поддон, большой коробок) помещается в автомобиль.
Но некоторые недостатки транспортной задачи можно обходить и применять ее в некоторых интересных случаях. Например, речь идет об аптечной сети. Руководители решили закрыть несколько нерентабельных аптек и открыть несколько новых. При этом весь ассортимент старых аптек надо перевести
вновые. Новые аптеки могут находиться совсем в других местах. Их количество может отличаться от количества закрываемых. Подразумевается, что некоторые группы препаратов можно группировать в крупные короба.
Или другой пример. Имеем крупную розничную сеть по продаже крупногабаритного товара (например, ортопедическое оборудование). В некоторых магазинах есть категории товаров, которые «залеживаются». А другие магазины, наоборот, чувствуют потребность в этом товаре. Математическая модель транспортной задачи следующая:
Z = ΣΣXijCij, при условиях:
ΣXij = Ai, |
i = 1, 2, … m; |
ΣXij = Bj, |
j = 1, 2, … n; |
Z → min,
34
где Z — затраты на перевозку грузов; X — объем груза; C — стоимость (тариф) перевозки единицы груза; A — запас поставщика; B — запрос потребителя; m — число поставщиков; n — число потребителей.
Решение задачи методом потенциалов происходит
внесколько этапов:
определение опорного решения;
применение к найденному опорному решению самого метода потенциалов;
проверка единственности решения.
Определение опорного плана, в свою очередь, можно выполнить несколькими способами:
метод северо-западного угла;
метод минимального элемента.
Опорный план определяется достаточно несложно. Методом северо-западного угла заполняем сначала верхнюю левую ячейку. Количество груза, которое в нее записываем, равно меньшому числу из двух: потребности первого магазина и запасам первого склада. Далее двигаемся как бы по диагонали (вниз и вправо), последовательно заполняя ячейки.
Витоге последней заполняется нижняя правая ячейка.
Вметоде минимального элемента первой заполнятся ячейка с минимальным тарифом. Дальше последовательно заполняется следующая из незаполненных ячеек с минимальным тарифом. При этом и в первом, и во втором методе, если мы заполнили ячейку количеством груза, которое полностью «покрывает» запас склада или потребность магазина, то строку (столбец) мы заполняем только одним числом, остальные ячейки строки (столбца) будут пустыми. Алгоритм метода потенциалов:
1. Построение первоначального опорного плана.
2. Определение потенциалов строк (пунктов отправленияj
(ui)) и столбцов (пунктов назначения (v)). Потенциалы находят,
решая систему уравнений: ui vj cij , где сij — тарифы, стоящие в заполняемых клетках таблицы. Для нахождения
35
решения системы один из потенциалов приравнивается произвольному числу (например, u1 = 0) и последовательно
находятся значения всех остальных потенциалов. Удобнее
вконце последовательно выписать все найденные потенциалы.
3.Проверка оптимальности плана. Проверяем выполнение
условия оптимальности: ui v j Cij для всех свободных клеток (где нет количества груза). Вычисляем ij = ui vj Cij —
оценки свободных переменных для оптимального базиса. Если все оценки свободных переменных для оптимального базисаij 0, то получаемый план является оптимальным, иначе —
к шагу 4.
4. Выбор свободной переменной (выбор клетки, в которую необходимо послать переменную). i0j0 max ij
среди ij 0. Если таких клеток несколько, то для заполнения
выбирается клетка, имеющая минимальный тариф.
5. Построение цикла пересчета для выбранной свободной клетки i0j0. Циклом в таблице условий ТЗ называется ломаная линия, которая начинается в свободной клетке и вершины которой (кроме начальной) расположены в занятых клетках, а звенья параллельны строкам и столбцам. После построения цикла его вершины последовательно отмечаются знаками «+» и «−», причем свободной клетке приписывается знак «+».
6. Определение величины перераспределения груза. d min xij , где xij — перевозки, стоящие в вершинах цикла, отмеченных знаком «−». Клетку, которой соответствует d, обозначим через i1j1.
7.Сдвиг по циклу пересчета (перераспределение грузов).
Ввыбранную для заполнения свободную клетку (i0,j0) заносится значение d. Одновременно это число прибавляется
к |
значениям перевозок, стоящих в клетках со знаком «+», |
и |
вычитается из значений перевозок, стоящих в клетках |
со знаком «−». Таким образом, клетка (i0,j0) становится занятой, а i1j1 — свободной.
36
8. Переход к шагу 2.
Приведем несколько примеров решения транспортных задач. Имеем три пункта отправления (склада) и четыре пункта назначения. Потребности и запасы в грузах соответствующих пунктов отправления и назначения представлены в табл. 10. Также в этой таблице на пересечении строк и столбцов приведены тарифы (стоимость перевозки одной единицы груза).
|
|
|
|
|
Таблица 10 |
|
|
|
|
|
|
|
|
Пункты отправления |
Пункты назначения |
Запасы |
|
|||
В1 |
В2 |
В3 |
В4 |
|
||
А1 |
1 |
2 |
4 |
1 |
50 |
|
А2 |
2 |
3 |
1 |
5 |
30 |
|
А3 |
3 |
2 |
4 |
4 |
10 |
|
Потребности |
30 |
30 |
10 |
20 |
90 |
|
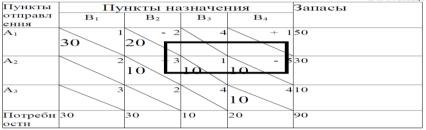
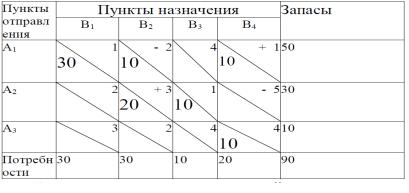
Составим таблицу транспортной задачи. Начальный план перевозок определим методом северо-западного угла (табл. 11). Для удобства тарифы будем записывать в правом верхнем углу, а количество груза — по центру.
Таблица 11
Затем определяем потенциалы пунктов отправления и потенциалы пунктов назначения. Для этого составляем уравнения для занятых клеток таблицы:
U1+V1=1,U1+V2=2,U2+V2=3, U2+V3=1,U2+V4=5, U3+V4=4. Пусть U1 = 0, тогда V1=1, V2=2, U2=1, V3=0, V4=4, U3=0.
37
Вычислим оценки ij для всех свободных клеток таблицы:
13 = 0 + 0 – 4 = −4, 14 = 0 + 4 – 1 = 3, 21 = 1 + 1 – 2 = 0, 31 = 0 + 1 − 3 = −2, 32 = 0 + 2 – 2 = 0, 33 = 0 + 0 – 4 = −4.
Выбираем максимальную положительную оценку. Это
оценка 14 = 3. Следовательно, на следующем шаге будет заполняться клетка с индексом 14. Составим цикл пересчета для данной клетки и пометим его вершины последовательно знаками «+» и «–».
Определим величину перераспределения груза как минимальную из величин, стоящих в минусовых клетках. Это 10 единиц. Прибавляем данную величину к величинам перевозок, стоящим в клетках со знаком «+» и вычитаем ее из величин перевозок, стоящих в клетках со знаком «–» (табл. 12).
Таблица 12
Составляем систему уравнений для определения потенциалов и последовательно находим из нее значения всех потенциалов.
U1+V1=1,U1+V2=2,U1+V4=1,U2+V2=3,U2+V3=1,U3+V4=4. Пусть U1=0, тогда V1=1, V2=2, U4=1, U2=1, V3=0, U3=3.
Вычислим оценки ijдля всех свободных клеток таблицы: Δ13=0+0−4= −4, Δ21=1+0−2= −1, Δ24=1+1−5= −3, 31=3+1-3= 1, 32=3+2−2= 3, 33=3+0−4= −1.
38

Максимальная положительная оценка |
32 = 3. Величина |
||
перераспределения груза равна 10 (табл. 13). |
Таблица 13 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Получили следующую таблицу (табл. 14).
Таблица 14
Составляем систему уравнений для определения потенциалов и последовательно находим из нее значения всех потенциалов.
U1+V1=1, U1+V2=2, U1+V4=1, U2+V2=3, U2+V3=1, U3+V2=2.
Пусть U1=0, тогда V1=1, V2=2, U4=1, U2=1, V3=0, U3=0.
Вычислим оценки ij для всех свободных клеток таблицы:
13=0+0−4= −4, 21=1+1−2= 0, 24=1+1−5= −3, 31=0+1−3= −2, 33=0+0−4= −4, 34=0+1−4= −3.
39
