Методическое пособие 549

УДК 517.2

Горбунов В.В., Соколова О.А. Начала математического анализа. Часть 2: Учеб. пособие. Воронеж: Воронеж. гос. техн.

ун-т, 2003. 108 с.

В учебном пособии излагаются элементы математического анализа. Теоретический материал иллюстрируется большим количеством примеров. Содержатся вопросы для самопроверки и задачи для самостоятельного решения.

Учебное пособие соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 657800 «Конструкторско-технологическое обеспечение машиностроительных производств», специальности 120200 «Металлобрабабативающие станки и комплексы», дисциплине «Математика».

Учебное пособие подготовлено на магнитном носителе в текстовом редакторе Microsoft Word и содержится в файле

“МатАн2.doc”.

Ил. 19. Библиогр.: 9 назв.

Научный редактор: д-р физ.-мат.наук, проф. В.Д. Репников

Рецензенты: кафедра естественно-научных дисциплин Международного института компьютерных технологий (зав. кафедрой канд. техн. наук, доцент Попов С.П.); д-р физ.мат.-наук, проф. В.А. Родин

Гобунов В.В., Соколова О.А., 2003 Оформление. Воронежский государственный технический университет, 2003

2

ВВЕДЕНИЕ

Современное машиностроительное производство предполагает наличие высокоразвитой системы технологического обеспечения. Компьютеризация конструкторско-технологической подготовки требует наличие хорошей математической подготовки.

Данное пособие продолжает серию пособий по высшей математике и посвящено изучению следующих разделов: комплексные числа, неопределенные интегралы, определенные интегралы.

Пособие имеет следующую структуру. В начале каждого параграфа приводятся соответствующие теоретические сведения (определения основных понятий, уравнения, формулы, правила, признаки, методы). Затем следуют вопросы для самопроверки и примеры решения типовых задач различной степени трудности. Далее предлагаются задачи для самостоятельного решения. Ко всем задачам даны ответы.

Учебное пособие соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 657800 «Конструкторско-технологическое обеспечение машиностроительных производств», специальности 120200 «Металлобрабабативающие станки и комплексы».

3

1. КОМПЛЕКСНЫЕ ЧИСЛА

1.1. Основные понятия

Среди действительных чисел не существует решений алгебраических уравнений с отрицательными значениями дискриминанта. Возникшая в математике потребность дополнить множество действительных чисел так, чтобы содержались все решения алгебраических уравнений, была

удовлетворена введением мнимой единицы ί 1 . Математический символ ί обозначает одно из решений

уравнения x2 1 0 и определяется соответствующими правилами действия над ним. Числа вида bί , где b является действительным числом, называются чисто мнимыми. Однако, наиболее общими числами, составленными с помощью мнимой

математический символ, который называется мнимой единицей: i2= 1.

Первая компонента a комплексного числа z a ί b

называется его действительной или вещественной частью и

обозначается a Re z . Вторая компонента b называется мнимой частью комплексного числа z a ί b и обозначается b Im z .

Комплексные числа имеют достаточно простой геометрический смысл. Выберем на плоскости декартову прямоугольную систему координат. Тогда каждой паре чисел (a,b) будет соответствовать на плоскости Oxy точка с

абсциссой a и ординатой b , рассматриваемая как геометрический образ комплексного числа z a ί b . Можно сказать, что каждому комплексному числу z a ί b будет соответствовать определѐнная точка (a,b) плоскости Oxy и,

4

наоборот, каждой точке (a,b) плоскости Oxy будет отвечать

определѐнное комплексное число z a ί b . Между множеством комплексных чисел и множеством точек плоскости Oxy существует взаимно однозначное соответствие.

Плоскость Oxy называется плоскостью комплексных чисел z . Действительные числа изображаются при этом точками оси Ox , которая называется действительной или

вещественной осью.

вектором, начало которого совпадает с началом координат, а конец – с точкой (a,b) .

1.2. Три формы записи комплексного числа

Запись комплексного числа в виде z x iy называется алгебраической формой представления комплексного числа z .

5

между положительным направлением действительной оси и

в виде, называемом тригонометрической формой записи

комплексного числа

Модуль комплексного числа определяется однозначно формулой

6

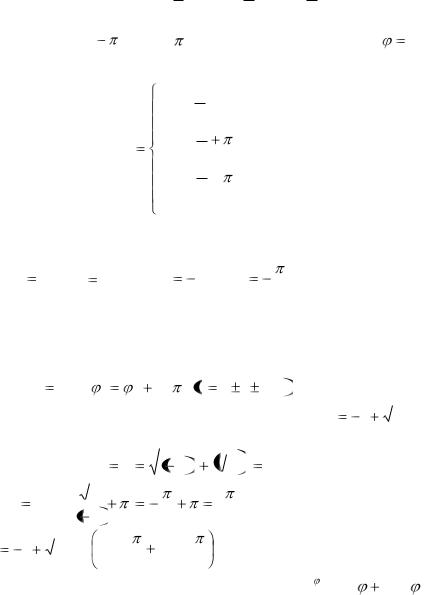
cos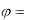rx , sin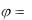ry , tg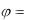xy .

arctg xy , для I, IV четвертей,

y

argz arctg x , для II четверти, arctg xy 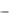, для III четверти.

тогда, когда равны их модули, а аргументы равны или отличаются на 2кπ:

7

комплексного числа к показательной или экспоненциальной форме:

функция ei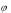 является периодической с основным периодом

2 .

Пример 1.2. Записать комплексное число z 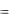1 ί в показательном виде.

1.3. Действия над комплексными числами

На множестве комплексных чисел определены действия, аналогичные действиям, определенным на множестве действительных чисел.

Суммой двух комплексных чисел z1 x1 iy1 и

z2 x2 iy2

называется число, определяемое равенством

т.е. при сложении комплексных чисел их действительные и мнимые части складываются. Сложение комплексных чисел обладает переместительным (коммутативным) и сочетательным (ассоциативным) свойствами:

Из вышеприведенного определения следует, что сложение комплексных чисел производится подобно сложению векторов (рис.2)

8

является действительным числом, равным квадрату модуля

переместительному, сочетательному и распределительному законам

Отсюда вытекает правило, что при перемножении комплексных чисел модули их перемножаются, а аргументы складываются.

При перемножении комплексных чисел в показательной форме вышеуказанное правило сохраняется, т.е.

10