Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

Математика

Файл:

Математика. уравнения и неравенства. Некрасова Н.Н., Горяйнов В.В.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.07 Mб

Скачать

☆

<<< < Предыдущая 12 / 62 3 4 5 6 > Следующая >>>

13.	x2 +6x +5 ≥ 0,		14.	(x +1)(x +7)≥ 0,
		x2 −6x −7 < 0.		(2 − x)(3 −	5x)≥ 0.

16.	3x −5 > 7,		17.	3x ≥ 0,
16.			17.
	2x +3 < 3.			x +7 < 0.
19.	−2x +2 ≥ 0,		20.	2x +1< 7,
19.			20.
	x +1 ≥ 0.			3x −1< −1.

15. x2x−4 > 0,2 +1

(x −2)(3 −4x)≤ 0.

x −2 > 0,

2x +1< 0.

4. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ

4.1. Свойства и графики показательной и логарифмической функций

практике

часто

используются

функции

вида

y = 2x ,

y =10x ,

и т. д., где аргумент является показателем степени,

y =

а основанием степени ‒ заданное число.

y = ax ( a > 0, a ≠1),

Определение. Функция, заданная формулой

называется показательной функцией с основанием a.

Показательную функцию также называют экспонентой по основанию a.

Сформулируем основные свойства показательной функции:

1º. Область определения функции

множество

всех действительных

чисел.

2º.

Область

значений функции

множество

всех положительных

действительных чисел: ax > 0,

x R .

3º.

При

a >1 функция возрастает на всей числовой прямой, т.е.

если

ax1 > ax2 ,

то

x > x

;

при

0 < a <1 функция убывает на множестве R , т.е.

если ax1 > ax2 , то

< x .

4º. Если

ax1

= ax2 ,

то

= x

5º. Производная функции: (ax )′ = ax ln a.

Выпишем основные характеристические свойства показательной функции (x, y R, a > 0, a ≠1) :

1º. ax a y = ax+y ;

2º. ax = ax−y ; a y

3º. (ax )y = axy .

А также часто используемые на практике свойства степеней (x, y R,

a > 0, a ≠1; b > 0, b ≠1) :

4º.(ab)x = ax bx ;

5º. a x

= ax

;

6º.

a−x =

;

7º. a0 =1;

8º. a1 = a .

График любой показательной

функции

y = ax

проходит через

точку

(0;1).

На рис. 4.1,а

представлен график показательной функции для случая

a >1 и при 0 < a <1 график функции изображен на рис. 4.1,б.

Определение.

Функция логарифм по основанию a

y = loga x

(x > 0)

является обратной для показательной функции y = ax .

Естественно,

при

этом остаются

ограничения

на

основание a :

a > 0,

a ≠1.

Сформулируем основные свойства логарифмической функции:

	1º. Область определения функции						множество			R всех положительных
действительных чисел.
	2º.	Область		значений функции		множество R				всех действительных
чисел.
	3º. При a >1 функция возрастает на всей области определения, т.е. если
x1 > 0,		x2 > 0	то	loga x1 > loga x2 ;	при		0 < a <1 функция убывает, т.е. если
x1 > 0,		x2 > 0	то	loga x1 < loga x2.
	4º. Если		loga x1 = loga x2, то		x1 = x2, x1 > 0,				x2 > 0.
	5º.	Возрастающая логарифмическая функция, будет положительной при
x >1,	и отрицательной при 0 < x <1.
	6º.	Убывающая логарифмическая функция,							будет отрицательной при
x >1,	и положительной при 0 < x <1.					1
	7º. Производная функции: (loga x)′ =					1		.
	7º. Производная функции: (loga x)′ =						x ln a	.
							x ln a

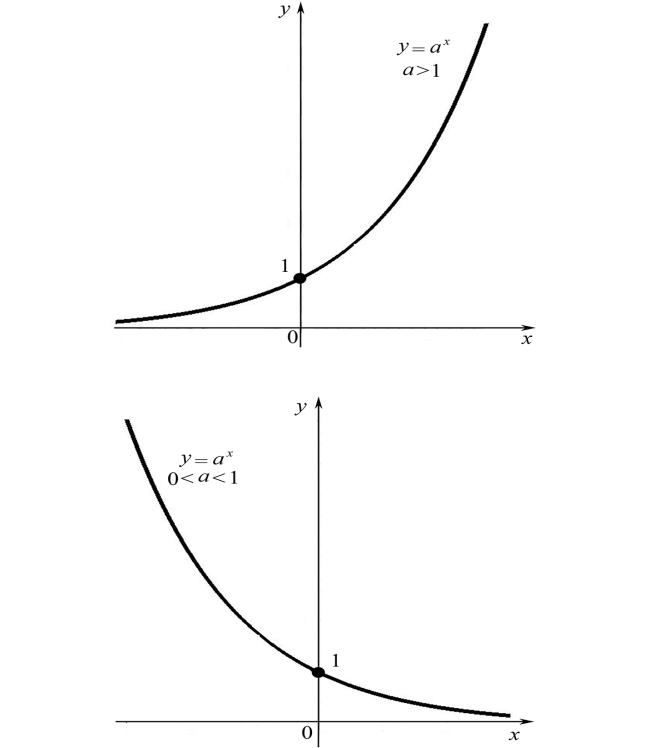
а)

б)

Рис. 4.1. Графическое изображение показательной функции: а) при a >1, б) при 0 < a <1

График любой логарифмической функции y = loga x		(x > 0, a > 0, a ≠1)
проходит через точку (1; 0).	На рис. 4.2, а	изображен график

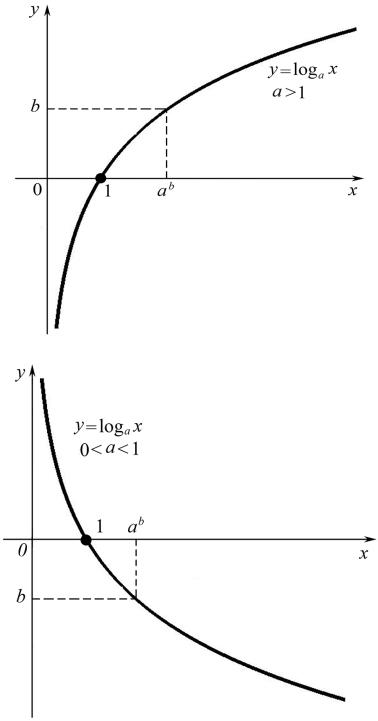
логарифмической функции для случая a >1, а для случая 0 < a <1 график представлен на рис. 4.2, б.

а)

б)

Рис. 4.2. Графическое изображение логарифмической функции: а) при a >1, б) при 0 < a <1

Показательная и логарифмическая функции не являются ни четными, ни нечетными; не имеет точек максимума и минимума; ни наибольшего, ни

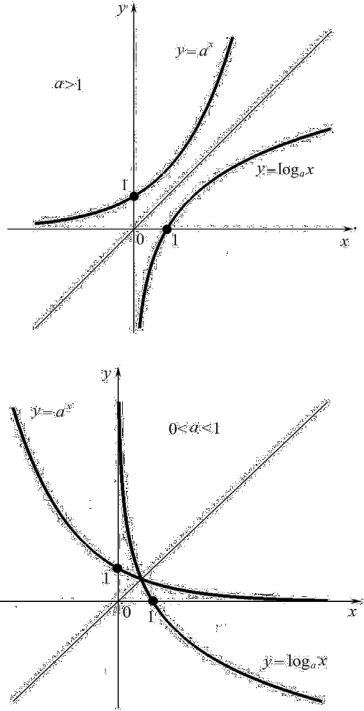
наименьшего значений; показательная функция ограничена снизу; логарифмическая функция не ограничена ни сверху, ни снизу. Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x . Данное утверждение показано на рис. 4.3: на

рис.4.3, а ‒ функции возрастающие, а на рис. 4.3, б ‒ убывающие.

а)

б)

Рис. 4.3. Графики показательной и обратной к ней логарифмической функций с одним основанием: а) при a >1, б) при 0 < a <1