УДК 624.94(07)

ББК 30.121

Составители: канд. техн. наук С.В. Ефрюшин, канд. техн. наук Н.А. Барченкова, С.А. Осипов

Оптимизация металлической рамы на стадиях упругого и пластического деформирования: методические указания к выполнению курсового проекта по дисциплине «Оптимизация и регулирование усилий в конструкциях» для магистрантов направления подготовки 08.04.01 « Строительство» (программа магистерской подготовки «Теория и проектирование зданий и сооружений») всех форм обучения / ФГБОУ ВО «Воронежский государственный

Основной целью указаний является пояснение содержания и порядка выполнения курсового проекта. Приводятся основные теоретические сведения и пример выполнения расчетной части курсового проекта с использованием системы инженерных и научных расчётов MATLAB и ПВК ЛИРА-САПР, а также перечень вариантов заданий, контрольные вопросы и библиографический список. Приводится текст компьютерной программы R-OPTIM, используемой в расчетах.

Предназначены для выполнения курсового проекта по дисциплине «Оптимизация и регулирование усилий в конструкциях» для магистрантов 2 курса.

Методические указания подготовлены в электронном виде и содержатся в файле RAMA OPTIM.pdf.

Ил. 17. Табл. 2. Библиогр.: 12 назв.

УДК 624.94(07)

ББК 30.121

Рецензент – С.Ю. Беляева, канд. техн. наук, доц. кафедры металлических и деревянных конструкций ВГТУ

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

ВВЕДЕНИЕ

В процессе обучения в магистратуре ВГТУ по направлению подготовки 08.04.01 « Строительство» профиль (специализация) «Теория и проектирование зданий и сооружений» при освоении дисциплины «Оптимизация и регулирование усилий в конструкциях» выполняется курсовой проект «Оптимизация металлической рамы на стадиях упругого и пластического деформирования». В настоящих методических указаниях излагается порядок выполнения курсового проекта, приводятся основные теоретические сведения, дается пример расчета с пояснениями и текстом компьютерной программы на языке инженерных и научных расчетов MATLAB для выполнения численных вычислений, а также перечень вариантов задания, контрольные вопросы и библиографический список.

1. Основные положения. Порядок выполнения курсового проекта

Цель задания – оптимизация металлической рамы* в предположении, что все стержневые элементы выполнены из одного и того же материала, поперечные сечения всех стоек с учетом унификации принимаются одинаковыми и неизменными по их длине - , аналогично и для ригелей - . В основу полагается расчет по несущей способности. Нагрузка ограничивается системой сосредоточенных сил и моментов. Для подбора сечений необходимо найти

Если предположить, что стоимости одного погонного метра стойки и ригеля выражаются через характеристики поперечных сечений и материала, из

которого они выполнены, т. е. и , то функция цели (1) принимает смысл стоимости всей рамы в целом:

* Примечание. Задача оптимального подбора параметров сечений, соответствующих определённому критерию качества называется проектной задачей или задачей оптимизации конструкции.

3

Полагая Uст = Uриг, получим другой вид целевой функции (1):

- для пластического.

Окончательной целью курсового проекта является сравнение расходов при изготовлении металлической рамы из упругого материала (при отсутствии остаточных деформаций) и материала идеально пластического. При оформлении курсового проекта рекомендуется придерживаться общепринятой последовательности изложения:

-Вводный раздел, где приводятся исходные данные, анализируются кинематические и геометрические свойства принятой к расчету рамы, формулируется математическая постановка задачи;

-Первый раздел «Оптимизация металлической рамы на стадии упруго-

нимается идеально пластическим (учитывается площадка текучести);

- Третий раздел «Выводы по результатам расчетов», где анализируются результаты расчётов и сравниваются значения целевой функции zупр и zпл.

При подготовке к сдаче курсового проекта необходимо ответить на контрольные вопросы, которые приводятся ниже.

1.1. Оптимизация металлической рамы на стадии упругого деформирования

В инженерной практике широко применяются расчёт и проектирование конструкций, основанные на учёте только упругой стадии деформирования материала, когда после разгрузки остаточные деформации не появляются. Такой подход обеспечивает возможность неоднократного нагружения стержневой системы в процессе эксплуатации.

4

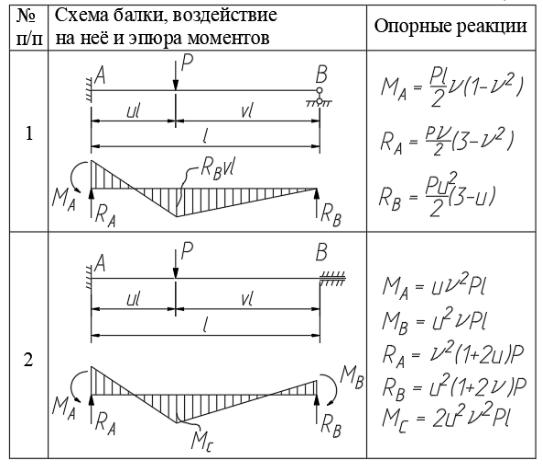
Решение основывается на итерационном алгоритме, в котором нулевая итерация выполняется вручную. При этом рама разбивается на систему стоек и ригелей, как отдельных балок. Для них с использованием таблицы 1 строятся эпюры изгибающих моментов и определяются Mmax ст и Mmax риг, по которым вычисляются моменты сопротивления (3) и назначаются размеры сечения стоек и ригелей исходя из назначенной преподавателем формы их сечений. В случае необходимости на нулевой итерации размеры сечений стоек и ригелей могут быть приняты одинаковыми.

Вычисления с построением эпюр изгибающих моментов на следующих итерациях выполняются методом конечных элементов на ПЭВМ с использованием программного комплекса ЛИРА-САПР. Подбор сечений, как на нулевой итерации, так и на каждой последующей выполняется вручную ( здесь и далее

на предыдущей итерации принимаются исходными для последующей. Итерационный процесс заканчивается, когда наибольшие изгибающие моменты в стержнях (и, как следствие, размеры поперечных сечений) стабилизируются, т.е. разница изгибающих моментов последующей и предыдущей итераций ста

5

нет менее 5%. Расчёты завершаются представлением окончательной эпюры изгибающих моментов, назначением размеров сечений по соотношению (3) и вычислением целевой функции zупр.

1.2. Оптимизация металлической рамы на стадии пластического деформирования

Расчёт конструкций с учётом пластических свойств материалов позволяет инженеру получить сведения о несущей способности при однократном нагружении, т. е. о наибольших нагрузках, при которых конструкция разрушается. Такая задача называется поверочной или задачей предельного равновесия.

Ниже приводятся основные теоретические сведения, необходимые для ознакомления с особенностями оптимизации плоской стержневой системы на стадии пластического разрушения.

1. При построении механико-математической модели оптимизации принимаются следующие основные допущения:

-прикладываемые нагрузки медленно возрастают пропорционально одному параметру, т. е. нагружение является простым, квазистатическим;

-материал стержней идеально пластический, изотропный;

-при пластическом разрушении деформации и перемещения малы, т. е. принимается геометрически линейная постановка задачи;

-сечения стержней имеют идеальную форму, и пластическое течение наступает одновременно по всей площади сечения;

-основным усилием, вызывающим пластическое разрушение, является изгибающий момент.

2. Переход сечения стержня в пластическое состояние сопровождается образованием, так называемого пластического шарнира. Пластический шарнир – это полностью перешедшее в пластическое состояние сечение, когда все нормальные напряжения, как в растянутой, так и в сжатой зоне равны пределу

текучести т (рис. 1). При этом под действием внешних усилий передаётся момент равный по абсолютной величине предельному изгибающему моменту сечения Мо

Т

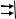
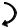МО

Т

Рис. 1. Пластический шарнир

6

Предельный изгибающий момент сечения Мо (пластический момент) понимается как равнодействующая предельных значений напряжений в сечении, когда напряжения во всем сечении достигают предела текучести. В результате потери внутренней связи сечение может свободно деформироваться, что допускает поворот первоначальной оси стержня на произвольный угол .

3. Задача оптимизации принимается в следующей формулировке: для заданной нагрузки и конфигурации рамы необходимо найти такое оптимальное распределение предельных усилий, при котором были бы удовлетворены критерий оптимальности в виде (1) или равносильном ему виде (2´) и условия состояния пластического разрушения для однократного нагружения.

Математической постановке задачи оптимизации предшествует формирование дискретной модели расчетной схемы рамы путем разделения ее расчетными сечениями на узлы и стержневые элементы. Назначение расчётных сечений связывается с образованием пластических шарниров в стержневой системе. Поэтому расположение расчётных сечений назначается в местах приложения сосредоточенных нагрузок, в местах, прилегающих к пересечениям (узлам) нескольких стержней и к опорам с жестким защемлением.

Несущую способность расчетных сечений характеризует вектор предельных моментов, компонентами которого являются модули соответствующих ве-

личин: { }

После определения степени статической неопределимости k назначается размерность m вектора обобщенных перемещений и усилий исходя из соотношения k = n – m, где для рамы, не имеющей замкнутых контуров, k = 2*Ш + С – 3*D, для рамы с замкнутыми контурами k = 3*К - Ш (К – число замкнутых контуров; Ш - число шарниров, С – число опорных связей; D – число дисков, соединяемых шарнирами).

Предельные изгибающие моменты для определённых групп сечений могут приниматься равными или с заданными соотношениями. В этом случае вводится матрица конфигурации G, которая формируется из элементов Gji = 1, если i-й предельный момент принадлежит j- му расчетному сечению, и Gji = 0 - в противном случае. Матрица G имеет размерность n x s, где s– размерность вектора Мо, т.е. число оптимизируемых параметров, рассматриваемых как число различных предельных моментов (s можно назначить минимальным, равным двум: по одному для каждой совокупности ригелей и стоек, но можно и максимальным, равным общему числу стержней в системе).

7

4. Основные соотношения.

Для рамы в целом записываются условия текучести, которые выражают требования не превышения изгибающих моментов в каждом расчётном сечении предельных моментов. В матричной форме они имеют вид:

где Е – единичная матрица размером n x n; Мо – вектор оптимизируемых параметров размерности s.

Усилия, возникающие в стадии пластического деформирования, должны удовлетворять уравнениям статики.

Вектор М называется статически допустимым, если в стадии пластического разрушения кроме условий текучести (4) он удовлетворяет уравнениям равновесия. Уравнения равновесия записываются в матричной форме:

(5)

где А – матрица коэффициентов уравнений равновесия; F – вектор нагрузок. Если вектор М удовлетворяет и условию текучести, то его называют ста-

тически возможным.

В теории пластичности и, в частности, в методе предельного равновесия важную роль играют скорости деформаций. В случае действия изгибающих моментов это вектор скоростей углов поворота сечений:

Величина равная абсолютному значению скалярного произведения вектора предельных моментов и вектора скоростей деформаций называется скоро-

стью диссипации энергии:

| ̇|.

Диссипация энергии положительная величина, её выражение записывается без знака абсолютного значения:

дующим энергетическим принципом: из всех статически допустимых векторов усилий при простом пластическом разрушении действительным будет тот, при котором скорость диссипации энергии (6) минимальна.

С целью однозначности решения поставленной задачи определения наименьшего объема материала (2´) без нарушения общности в силу произ-

ленный из длин стержней рамы. Тогда выражение экстремального энергетического принципа примет вид целевой функции задачи оптимизации в статической формулировке с дополнительными условиями (4), (5):

{

Задача (7) является задачей линейного программирования в силу линейности всех входящих в нее соотношений.

Другой энергетический принцип двойственный представленному выше основывается на понятии мощности нагрузки, которая означает скалярное произведение вектора нагрузки на вектор скоростей перемещений:

̇ ̇

В стадии пластического деформирования скорости деформаций должны удовлетворять геометрическим уравнениям.

Кинематически допустимым вектором скоростей перемещений (деформаций) называется вектор, удовлетворяющий геометрическим уравнениям и дополнительным условиям нормализации, например фиксированной скорости диссипации энергии или мощности нагрузки. Вектор скоростей перемещений (деформаций) называется кинематически возможным, если удовлетворяет геометрическим уравнениям

Двойственный экстремальный энергетический принцип формулируется следующим образом: из всех кинематически допустимых векторов скоростей перемещений и деформаций при простом пластическом разрушении действительными являются те, при которых мощность нагрузки максимальна.

Полную формулировку двойственной задачи получают методом неопределённых множителей Лагранжа. Из решения двойственной задачи определяются скорости деформаций и перемещений (конфигурация механизма разрушения). Задача оптимизации в кинематической (двойственной) формулировке записывается в виде:

Задача (8) также как и задача (7) является задачей линейного программирования.

5. Совместное решение задач линейного программирования (7) и (8) позволит определить: распределение предельных моментов по расчётным се-

9