
Методическое пособие 514
.pdf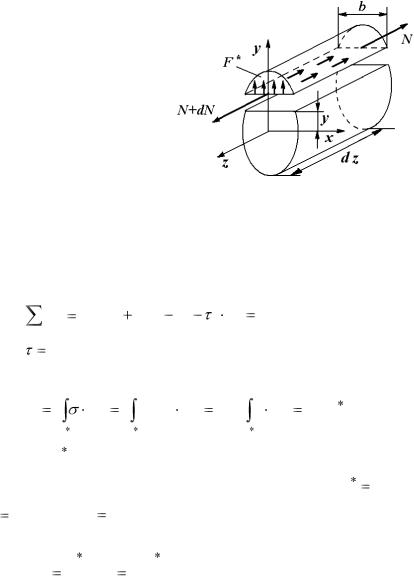
Двумя близкими поперечными сечениями вырежем часть балки длиной dz (рис. 4.14). Мысленно разрежем балку, испытывающую изгиб, продольным сечением. Рассмотрим равновесие верхнего элемента площадью
сечения F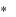 и шириной основания b , приложив к
и шириной основания b , приложив к
нему нагрузки со стороны отброшенных частей. Касательные напряжения 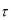 на взаимноперпендикулярных гранях равны и направлены от общего ребра, согласно теореме парности. Составим уравнение равновесия:
на взаимноперпендикулярных гранях равны и направлены от общего ребра, согласно теореме парности. Составим уравнение равновесия:
|
Piz |
0 : (N dN ) N b dz 0 , |
|
|
|
||||||||||||
|
|
|
1 |
|
dN |
. |
|
|
|
|
|
|
|
|
(4.33) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
b dz |
|
|
|
|
|
|
|
|
||||||
Подставим (4.32) в (4.10): |
|
|
|
|
|
||||||||||||
|
N |
|
|
dF |
|
M |
y dF |
M |
y dF |
M |
Sx , |
(4.34) |
|||||
|
|
|
|
|
|||||||||||||
|
|
|
F |
|
|
|
F |
J x |
|
J x |
F |
J x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где S x – статический момент площади. |
|
|
|
||||||||||||||
Полагая балку |
постоянного |
сечения, т.е. S x |
const , |
||||||||||||||
J x const , |
M M (z) , продифференцируем (4.35) по |
||||||||||||||||
координате z с учетом 1-ой теоремы Журавского (4.4): |
|
||||||||||||||||
|
dN |
|
Sx dM |
Q |
Sx |
. |
|
|
|
|
(4.35) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dz |
|
J x dz |
J x |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
Подставим (4.35) в (4.33):
80

Q S x |
. |
(4.36) |
|||
|
|
|
|||
b J x |
|||||
|
|
||||
Это формула Журавского.
4.5.2. Расчёт на прочность при поперечном изгибе
Для нормальных напряжений проводится по тем же критериям, что и при чистом изгибе:
|
|
|
|
M |
|
|
ymax |
|
M |
|
[ ] . |
|
|||||
max |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Wx |
|
|||||||
|
|
|
|
|
J x |
|
|
|
|
||||||||
(4.37) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Расчет по касательным напряжениям, как правило, |
|||||||||||||||||
делается проверочным: |
|
|
|
|
|
||||||||||||
|
|
|
|
Q |
|
S |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
max |
|
|
|
|
|
|
|
|
|
x |
[ ] . |
|
(4.38) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
b J x |
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Обычно, согласно экспериментальному соотношению: |
|||||||||||||||||
[ ] |
|
0.58[ ] . |
|
|
|
(4.39) |
|||||||||||
|
4.6. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ |
||||||||||||||||
|
|
|
|
|
|
4.6.1. Виды перемещений при изгибе |
|
||||||||||
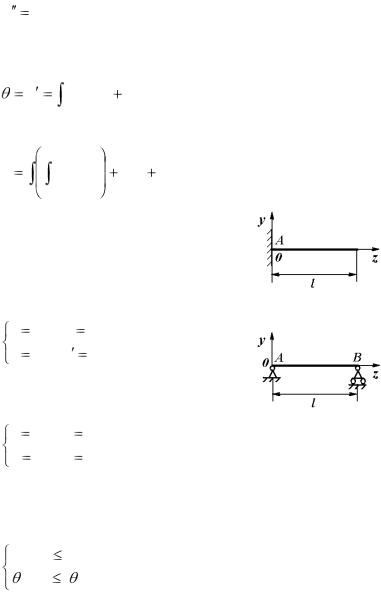
Рассмотрим |
деформацию |
||||||||||||||||
консольной балки под действием |
|||||||||||||||||
силы P , |
испытывающей |
изгиб |
|||||||||||||||
(рис. 4.15). Изогнутая ось балки |
|||||||||||||||||
является геометрическим местом |
|||||||||||||||||
центров |
тяжести |
поперечных |
|||||||||||||||
сечений деформированной балки |
|
||
и называется упругой линией. На |
|
||
произвольном |
расстоянии z |
|
|
проведём поперечное сечение B . |
|
||
В точке B1 |
упругой |
линии |
Рис. 4.15 |
проведём касательную |
и нормаль |
n , которая совпадает с |
|
плоскостью поперечного сечения изогнутой балки в точке B1 .
81

Для описания деформации балки в плоскости yz используются две характеристики:
1)прогиб y – линейное вертикальное перемещение BB1 центра тяжести сечения;
2)угол поворота сечения 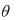 – угол, на который поворачивается поперечное сечение балки относительно его первоначального положения.
– угол, на который поворачивается поперечное сечение балки относительно его первоначального положения.
Вследствие малости углов:
tg |
|
|
|
|
dy |
y . |
(4.40) |
|||
|
|
|
|
|
|
|||||
|
|
|
|
dt |
||||||
|
|
|
|
|
|
|
|
|
||
|
4.6.2. Дифференциальное уравнение упругой линии |
|||||||||
|
|
|
|
|
|
|
|
|
|
балки |
При выводе формулы для напряжения при чистом |
||||||||||
изгибе было получено: |
|
|||||||||
|
E |
M x |
. |
|
|
|
|
|||
|
|
|
J x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
где |
|
|
ds |
|
– радиус кривизны балки. |
|||||
|
d |
|
||||||||
|
|
|
|
|
|
|
||||
Отсюда: |
|
|
|
|
|
|
||||
1 |
|
M x |
|
. |
|
|
(4.41) |
|||
|
|
|
|
|
|
|
|
|||
|
|
|
EJ x |
|
|
|
||||
Величина |
EJ x |
const называется жёсткостью балки |
||||||||
при изгибе (изгибная жесткость).
Из дифференциальной геометрии кривизна кривой в точке равна:
k |
1 |
|
y |
|
|
|
|
. |
|
|
(1 ( y )2 )3 2 |
|||
известно, что
(4.42)
Учитывая, что перемещения малы и y |
1, получаем: |
||
1 |
y . |
(4.43) |
|
|
|
||
|
|
||
82
Подставим (4.43) в (4.11) и получим дифференциальное уравнение упругой линии балки:
y |
M x |
. |
(4.44) |
|
EJ x |
||||
|
|
|
Интегрируя (4.44) и учитывая (4.40), получим уравнение углов поворота:
|
|
y |
|
|
M x |
|
dz |
C . |
|
|
|
|
(4.45) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
EJ x |
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегрирование (4.45) даёт уравнение упругой линии: |
|||||||||||||||||
|
y |
|
|
|
M x |
|
dz |
C z |
C |
2 |
. |
|
(4.46) |
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
EJ x |
|
|
1 |
|
|
|
|
|||||
|
|
l |
l |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Для |
|
|
определения |
неизвестных |
|
||||||||||||
констант интегрирования C1 |
и C2 |
нужны |
|
|||||||||||||||
граничные условия. |
|
|
|
|
|
|
|
|
||||||||||
|
Для консольной балки (рис. 4.16) |
|
||||||||||||||||
граничные условия имеют вид: |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.16 |
|
|
z |
0 : |
|
|
y |
0; |
|
|
|
|
(4.47) |
|
|||||
|
|
z |
0 : |
|
y |
|
|
0. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Для шарнирно-опертой балки (рис. |
|
||||||||||||||||
4.17) |
|
граничные |
|
|
условия |
|
|
можно |
|
|||||||||
представить в форме: |
|
|
|
|
|
|
||||||||||||
|
|
z |
0 : |
|
|
y |
0; |
|
|
|
|
(4.48) |
Рис. 4.17 |
|||||
|
|
z |
l : y |
0. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4.6.3. Условие жёсткости при изгибе |
||||||||||||
|
Деталь жёсткая, если выполняются условия |
|||||||||||||||||
жесткости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ymax |
|
|
|
[ y], |
|
|
|
|
|
|
|
(4.49) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
max |
|
|
|
[ |
], |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
83
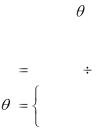
где [ y] и [ ] – допускаемые значения прогиба и угла
поворота, задаваемые из конструктивных и технологических соображений. Обычно
[ y] (0.0001 0.0004)l ,
[ ] |
0.01 рад |
для шарикоподшипников; |
|
0.001 рад |
для роликовых подшипников. |
||
|
По условиям жесткости (4.53) выполняют те же виды расчетов, что по условию прочности (4.20).
4.7. ЭПЮРЫ ВНУТРЕННИХ СИЛ ПРИ ИЗГИБЕ
При решении статически определимых задач используется следующий алгоритм:
1)Определение сил реакций (при необходимости) из условий равновесия.
2)Разбиение вала на участки. Границами участков являются сечения, в которых приложены сосредоточенные силы, приложены сосредоточенные моменты, начинается/заканчивается распределенная нагрузка, меняется геометрия сечения.
3)Составление уравнений для перерезывающей силы и момента на участках.
4)Построение эпюр Q(z) и M (z) .
5)Проверка на прочность и жёсткость.
Если рассчитывается статически неопределимая балка, то дополнительно надо провести раскрытие статической неопределимости: установить степень статической неопределимости; рассматривая схему деформирования балки; составить уравнение совместности перемещений; в уравнении совместности перемещений заменить углы поворота сечений через крутящие моменты и жесткости ступней вала.
84
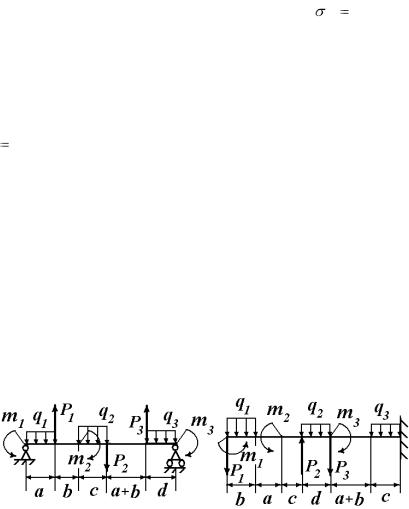
4.8. ЗАДАЧА И1 К КОНТРОЛЬНОЙ РАБОТЕ
Консольная или духопорная стальная балка, нагружена сосредоточенными силами Pi , распределенной нагрузкой
интенсивностью qi и внешними моментами mi (рис. И1.0– И1.9). Марка стали: Ст. 3, предел текучести T 225 МПа.
Определить силы реакции. Построить эпюры поперечной силы и изгибающего момента в поперечном сечении балки. Определить из условия прочности размеры сечения для балки
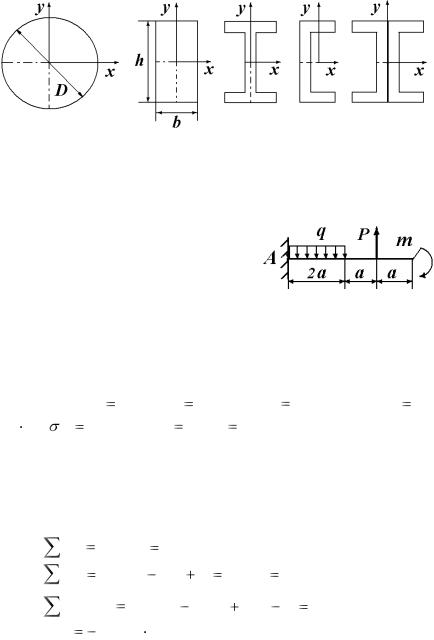
(рис. И1):
а) круглого сплошного сечения (диаметр D );
б) прямоугольного сечения (размеры b и h , считая h 1,5b );
в) двутавра; г) швеллера;
д) поставленных друг к другу вплотную одинаковых несвязанных швеллеров.
Выбрать рациональное сечение, проведя оценку коэффициентов экономичности.
Численные данные приведены в таблице Р1, где n – коэффициент запаса прочности.
Указания. Задача И1 – на расчет на прочность при изгибе статически определимой балки. Решение задачи проводится в соответствии с алгоритмом, описанным в разделе 4.7. Ход решения подобной задачи приведен в примере И1.
Рис. И1.0 |
Рис. И1.1 |
85
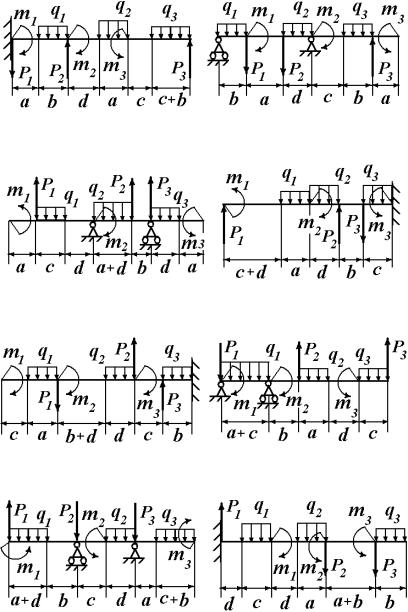
Рис. И1.2 |
Рис. И1.3 |
Рис. И1.4 |
Рис. И1.5 |
Рис. И1.6 |
Рис. И1.7 |
Рис. И1.8 |
Рис. И1.9 |
86

Таблица И1
№ |
a , |
b |
c |
d |
P1 |
P2 |
P3 |
m1 , |
m2 , |
m3 , |
q1 |
q2 |
q3 |
|
q , |
|
||
|
|
|
||||||||||||||||
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,8 |
1,2a |
0,5a |
2a |
qa |
|
|
|
|
3qa 2 |
|
|
|
2q |
|
5 |
|
|
1 |
1 |
0,5a |
1,2a |
0,4a |
|
2qa |
|
|
|
|
|
4qa 2 |
5q |
|
|
|
10 |
|
2 |
0,2 |
0,4a |
0,3a |
0,8a |
|
|
6qa |
2qa |
2 |
|
|
|
|
7q |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1,4 |
0,6a |
0,8a |
0,5a |
8qa |
|
|
|
|
|
|
6qa 2 |
|
4q |
|
|
9 |
|
4 |
0,5 |
1,2a |
2a |
1,5a |
|
7qa |
|
3qa 2 |
|
|
|
|
|
6q |
|
8 |
|
|
5 |
0,6 |
2a |
1,4a |
1,6a |
|
|
2qa |
|
|
5qa 2 |
|
6q |
|
|
|
11 |
|
|
6 |
0,3 |
3a |
4a |
2a |
|
|
5qa |
qa 2 |
|
|
|
|
8q |
|
|
7 |
|
|
7 |
0,9 |
1,5a |
1,1a |
1,2a |
4qa |
|
|
|
|
2qa |
2 |
|
|
|
q |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
1,1 |
0,8a |
1,3a |
1,7a |
|
qa |
|
4qa 2 |
|
|
|
|
|
5q |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
9 |
0,7 |
0,9a |
1,6a |
1,1a |
|
3qa |
|
|
|
|
|
qa 2 |
4q |
|
|
|
12 |
|
87
а) |
б) |
в) |
г) |
д) |
Рис. И1
Пример И1. Консольная стальная балка нагружена сосредоточенной силой, распределенной нагрузкой и моментом (рис. 4.18). Определить реактивный и наибольший крутящий
момент. Построить эпюры Рис. 4.18 поперечной силы и изгибающего момента. Определить из условия прочности размеры сечения для балки (рис. И1) и выбрать рациональное
Дано: |
a 1 м , P |
40 |
кН , q 20 кН / м , m 60 |
кН м , T |
225 МПа, n |
1,2 , h |
1,5b . |
Решение:
1) Определяем силы реакции. Балка защемлена с одной стороны. Отбрасываем жёсткую заделку, заменяя её реактивным моментом M A и силами реакции YA и Z A (рис. 4.19 а). Составим уравнения равновесия:
Piz |
0 : |
Z A |
0 ; |
|
|
||||
Piy |
|
0 : YA |
2qa P 0 , YA 0 ; |
|
|||||
|
|
|
|
|
|
|
2qa 2 3Pa m 0 |
|
|
m |
A |
(P ) 0 : |
M |
A |
, |
||||
|
|
i |
|
|
|
|
|||
M A |
|
20 |
кН м . |
|
|
|
|||
|
|
|
|
|
|
|
|
88 |
|
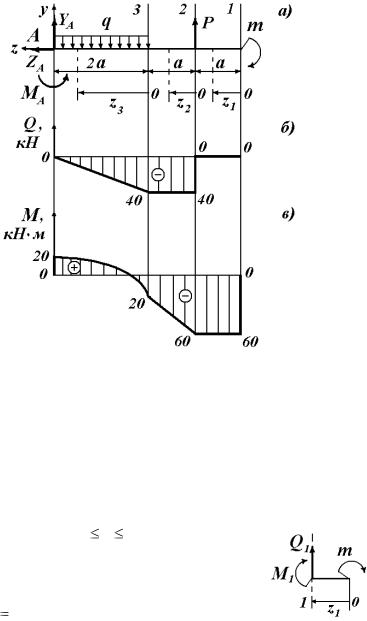
Рис. 4.19
2) Разобьем вал на 3 участка. Границами участков являются сечения, в которых приложены сосредоточенные силы, приложены сосредоточенные моменты, начинается/заканчивается распределенная нагрузка, меняется геометрия сечения. На каждом участке запишем выражение для перерезывающей силы и изгибающего момента.
1 |
участок: 0 z a . Рассечем этот |
|
участок произвольным поперечным сечением |
|
|
z1 (рис. 4.20). |
|
|
Перерезывающая сила |
|
|
Q1 |
0 . |
|
Изгибающий момент |
Рис. 4.20 |
|
|
|
|
|
89 |
|
