Методическое пособие 445

ФГБОУ ВПО «Воронежский государственный технический университет»

Кафедра систем информационной безопасности

ЦИФРОВЫЕ СХЕМЫ ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям по дисциплине «Электроника и схемотехника» для студентов специальностей

090301 «Компьютерная безопасность»,

090302 «Информационная безопасность телекоммуникационных систем», 090303 «Информационная безопасность автоматизированных систем»

очной формы обучения

Воронеж 2015

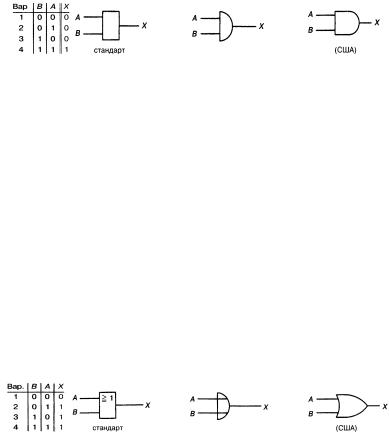
Условные обозначения двухвходового элемента И приведены на рис. 1. б-г.

На выходе логического элемента И сигнал 1 появится тогда, когда на всех входах совпадут сигналы 1.

а б в г Рис. 1. Логический элемент И

На выходе логического элемента И сигнал 1 появится тогда, когда на всех входах совпадут сигналы 1.

Логический элемент ИЛИ

Для обозначения операции ИЛИ (дизъюнкция) в алгебре логики используется символ или +:

Этой операции соответствует таблица истинности, приведенная на рис. 2 а. Условные обозначения двухвходового элемента И приведены на рис. 2 б-г.

На выходе логического элемента ИЛИ сигнал 1 появится только тогда, когда хотя бы на одном из его входов присутствует сигнал 1.

3

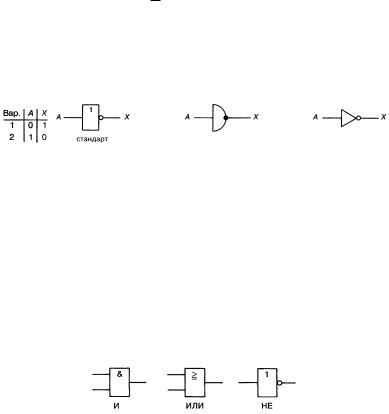
Логический элемент НЕ

Для обозначения операции НЕ (инверсия) в алгебре логики используется черта над символом, апостроф и знак ¬ перед символом.

противоположно состоянию входа.

Логические элементы И, ИЛИ и НЕ предназначены для выполнения трех основных операций цифровой логики над дискретными сигналами. С помощью этих элементов можно реализовать логические операции любой сложности. Поэтому эти элементы называются основными (рис. 4).

Рис. 4. Стандартизованные графические обозначения элементов

Комбинированные элементы Логический элемент И-НЕ

Если соединить последовательно элементы И и НЕ согласно схеме на рис. 5 а, то выход X логического элемента И

4

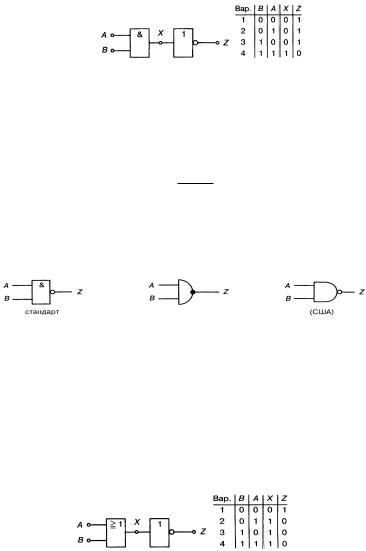
инвертируется. Этой операции соответствует таблица истинности, приведенная на рис. 5 б.

а б Рис. 5. Логический элемент И-НЕ

Условные обозначения двухвходового элемента И-НЕ приведены на рис. 6 а-в.

На выходе логического элемента И-НЕ логическая 1 будет только в том случае, если не на всех входах наступает состояние 1.

Логический элемент ИЛИ-НЕ

Схема элемента ИЛИ-НЕ приведена на рис. 7 а, соответствующая ей таблица истинности – на рис. 7 б.

а б Рис. 7. Элемент ИЛИ-НЕ

5

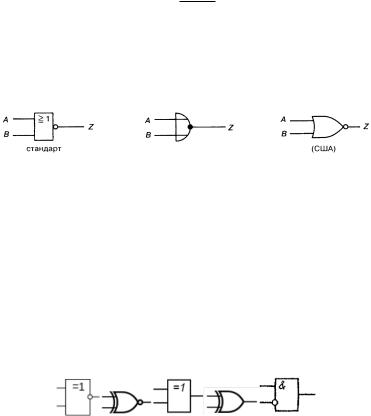
Логическая функция элемента ИЛИ-НЕ:

Z A B .

Условные обозначения двухвходового элемента ИЛИ-НЕ приведены на рис. 8 а-в.

На выходе логического элемента ИЛИ-НЕ логическая 1 будет только в том случае, если ни на одном из входов нет состояния 1.

Равнозначность

Элемент «Равнозначность» (эквивалентность, исключающее ИЛИ-НЕ) (рис. 9, а) имеет на выходе логическую 1, если на входах одновременно воздействуют одинаковые логические переменные.

6

Неравнозначность

Элемент «Неравнозначность» (исключающее ИЛИ, сложение по модулю 2) (рис. 9, б) имеет на выходе логическую 1, если на входах присутствуют неравнозначные логические переменные. Для обозначения операции используются знаки:

Запрет

Элемент «Запрет» (рис. 9 в) имеет на выходе логическую 1, если на основном входе воздействует логический сигнал x1 = 1, а на запрещающем входе – логический сигнал x2 = 0

F x1 x2 x1 x2 .

Если необходимы три входа или более, то соединяют последовательно двухвходовые элементы (рис. 10)

Рис. 10. Последовательное соединение элементов

С добавлением каждого нового входа число комбинаций (вариантов вход-вход) таблицы истинности удваивается.

Для реализации логических операций применяют соответствующие логические элементы. Система элементов,

7

позволяющая строить на их базе логическую схему любой сложности, называется функционально полной системой элементов или базисом. Базис образуют логические элементы ИЛИ, И и НЕ. Кроме того, на практике широко применяются логические элементы, реализующие простейшие функции двух аргументов ИЛИ–НЕ (стрелка Пирса – x1 ↓ х2) (рис. 13.1, г), И– НЕ (штрих Шеффера – x1 / х2) [3].

Аксиомы алгебры логики

инверсии (теоремы де Моргана)

X1 X2 X3 X1 X2 X3

Логическую функцию для удобства записи и последующего синтеза схемы выражают в виде суммы

8

произведений переменных либо в виде произведения их сумм

[1].

Запись логической функции в виде суммы произведений переменных или их инверсий называют дизъюнктивной нормальной формой (ДНФ). ДНФ может быть получена из таблицы истинности. Для этого для значений функции Y = 1 записываются элементарные логические произведения. Запись функции в виде произведения сумм называется конъюнктивной нормальной формой (КНФ). КНФ может быть получена из таблицы истинности. Для этого для значений функции Y = 0 записываются элементарные логические суммы входных величин.

Для каждой логической функции может существовать несколько равносильных ДНФ и КНФ. Вместе с тем имеется только один вид ДНФ или КНФ, в котором функция может быть записана единственным образом (совершенные нормальные формы).

В совершенной дизъюнктивной нормальной форме

(СДНФ) каждое входящее слагаемое включает все переменные (с инверсиями и без них) и нет одинаковых слагаемых. В

совершенной конъюнктивной нормальной форме (СКНФ)

каждый входящий сомножитель включает все переменные (с инверсиями и без них) и нет одинаковых сомножителей.

Любую логическую схему можно описать и представить в ДНФ или КНФ. Однако полученная таким образом схема не является оптимальной с точки зрения ее практической реализации. Поэтому исходные логические функции обычно минимизируют. Целью минимизации является уменьшение стоимости ее технической реализации. Критерий минимизации неоднозначен. Наиболее просто задача минимизации решается с использованием карт Вейча (рис. 11). Для минимизации несложных функций применяются алгебраические преобразования. Для функций, имеющих большое число переменных (больше трех) и большое число слагаемых, – специальные методы [1].

9