
Методические указания к практическим занятиям по дисциплине «Криптографические методы защиты информации». Мокроусов А.Н
.pdf
Вычисленные остатки и нулевые элементы α0 - α14 поля Галуа GF (24) сведены в табл. 8.
Таблица 8
Xi |
Остаток |
αi |
Х0 |
0001 |
α0 |
X1 |
0010 |
α1 |
X2 |
0100 |
α2 |
X3 |
1000 |
α3 |
X4 |
0011 |
α4 |
X5 |
0110 |
α5 |
X6 |
1100 |
α6 |
X7 |
1011 |
α7 |
X8 |
0101 |
α8 |
X9 |
1010 |
α9 |
X10 |
0111 |
α10 |
X11 |
1110 |
α11 |
X12 |
1111 |
α12 |
X13 |
1101 |
α13 |
X14 |
1001 |
α14 |
Поле Галуа GF (24) построено как поле многочленов с коэффициентами 0 и 1 по модулю неприводимого многочлена:
29

Р(Х4)=Х4 + Х + 1<--> 10011.
В поле Галуа GF (2n) определены четыре алгебраические операции. Операции сложения и вычитания выполняются как операции поразрядного сложения по модулю 2; операция умножения элементов поля выполняется как умножение соответствующих многочленов с приведением по модулю неприводимого многочлена Р(Х), т. е. многочлена, по модулю которого построены элементы поля GF (2n).
Пример. α5 = 0110, α6 = 1100, α5+ α6 = 1010, так как
Пример. α14 = 1001,
α14 * α14 = α214= α13 по mod Р1(Х4) <-->1 0 0 1 1.
Чтобы выполнить деление элемента b на элемент а в поле модулю Р (Х), сначала находят обратный элемент a-1(mod P (X)), а затем вычисляют
b * a-1(mod P (X)).
Каждый двоичный вектор длиной n, исключая 0, является взаимно простым с неприводимым многочленом Р (Х) независимо от значения Р (Х). Поэтому число вычетов, взаимно простых с Р(Х), равно φ(Р(Х)) = 2n - 1 (расширение функции Эйлера для многочленов). Поэтому
30
a-1= aφ(P(X))-1 mod Р(Х) = 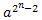 mod P(Х)
mod P(Х)
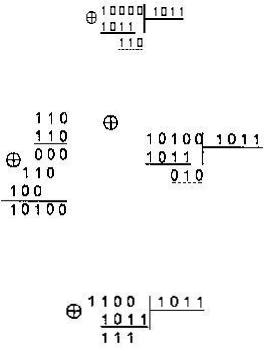
Пример. Пусть a = 100 и P(X) = 1011 в поле GF (23).
a-1= 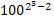 (mod 1011) = 1006 (mod 1011) = 1002 * 1004(mod 1011).
(mod 1011) = 1006 (mod 1011) = 1002 * 1004(mod 1011).
1002 (mod 1011) = 10000  10110 = 110.
10110 = 110.
или
1004 (mod 1011) = 1102 (mod 1011) = 010.
или
1002 * 1004 (mod 1011)= 110 * 010 (mod 1011) = = 1100 (mod 1011) = 111.
или
Итак, a-1 = 111.
Проверка: a=100, a-1 = 111, P(X)=1011, a*a-1=110*100=11100.
31
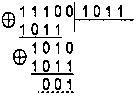
т. е. a*a-1(mod 1011) = 1.
Достоинства вычислений в поле GF (2n):
Все элементы поля Галуа имеют конечный размер, деление элементов не имеет каких-либо ошибок округления.
Сложение и вычитание элементов поля GF (2n) не требует деления на модуль.
Алгоритмы вычислений в поле GF (2n) допускают параллельную реализацию.
Для поля GF (2n) обычно применяют в качестве модуля трехчлен Р (Хn) = Хn + Х + 1.
Длинная строка нулей между коэффициентами при Xn и X обеспечивает более простую реализацию быстрого умножения (с приведением по модулю). Трехчлен Р (Хn ) должен быть неприводимым и примитивным.
Трехчлен Р (Хn)= Хn + Х + 1 является примитивным для следующих значений n (n<1000):
1, 3, 4, 6, 9, 15, 22, 28, 30, 46, 60, 63, 127, 153, 172, 303, 471, 532, 865, 900.
Контрольные вопросы:
1.Что такое конечное поле?
2.В чём смысл свойств многочленов и их корней в двоичном поле GF (2)?
32
3.Каковы достоинства вычислений в поле GF (2n)?
4.На практике способы шифрования подстановки и перестановки, как правило, применяются одновременно. Привести практические примеры способов защиты информации, которые относятся к симметричным системам защиты данных.
5.Какие существуют разновидности относительно метода перестановки?
6.Сравните между собой два способа шифрования подстановки и перестановки. Укажите преимущества и недостатки каждого из них.
33
Практическое занятие № 8 Тестирование простоты числа методом перебора делителей
Перебор делителей – это алгоритм, применяемый для определения, какое число перед нами: простое или составное
[4].
Алгоритм заключается в последовательном делении заданного натурального числа на все целые числа, начиная с двойки и заканчивая значением меньшим или равным квадратному корню тестируемого числа. Если хотя бы один делитель делит тестируемое число без остатка, то оно является составным. Если у тестируемого числа нет ни одного делителя, делящего его без остатка, то такое число является простым. Блок-схема данного алгоритма представлена на рис. 2.
Контрольные вопросы:
1.В чем смысл алгоритма перебора делителей?
2.Какова блок-схема алгоритма перебора делителей?
3.Приведите недостатки метода шифрования на примере ситуации, когда результатом атаки служит фрагмент исходного текста и соответствующей криптограммы.
4.Разработать алгоритм синтеза криптосистемы, в основе которой лежат сами Р-ичные представления элементов шифра в системе счисления с основанием Р.
5.Разработать алгоритм определения всех слов кода Варшамова Wn. Зависит ли количество кодовых слов от параметра a?
6.Разработать алгоритм атаки для определения секретного ключа заданной системы защиты информации:
а) по известной криптосистеме длины N; б) по известному вектору B = (b1, b2, … ,bn).
34
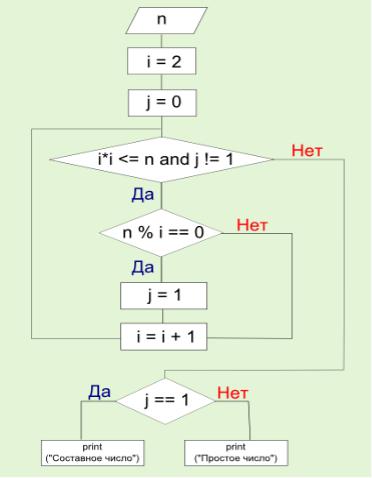
Рис. 2. Алгоритм «Перебор делителей»
35
Практическое занятие № 9 Разложение на множители
Разложить число на множители - значит найти его простые сомножители [4].
10 = 2*5
60 = 2*2*3*5 252601=41*61*101
2113- 1 =3391*23279*65993*1868569*1066818132868207
Разложение на множители является одной из древнейших проблем теории чисел. Этот процесс несложен, но требует времени. Это пока остается так, но ряд сдвигов в этом искусстве все же произошел.
Решето Эратосфена – это алгоритм нахождения простых чисел до заданного числа n. В процессе выполнения данного алгоритма постепенно отсеиваются составные числа, кратные простым, начиная с 2. Блок-схема данного алгоритма представлена на рис. 3.
Контрольные вопросы:
1.Что означает разложить число на множители?
2.В чём смысл решета Эратосфена?
3.Доказать, что любое десятичное число можно представить в p-ичной системе счисления единственным способом.
4.Оценить время, необходимое для перевода заданного целого числа в систему счисления с основанием b.
5.Разработать алгоритм для нахождения целочисленного решения уравнения Х2 + Y2 = n, где n – некоторое заданное положительное число. Определить его временную сложность.
36
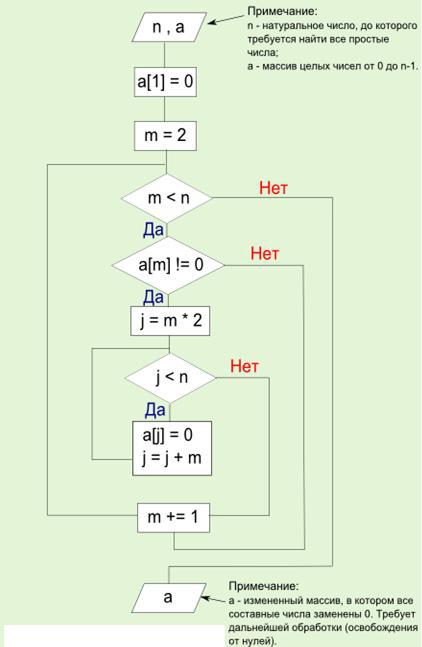
Рис. 3. Алгоритм «Решето Эратосфена»
37
Практическое занятие № 10 Символы Лежандра и Якоби
Символ Лежандра, L(a,p), определен, если a - это любое целое число, а p - простое число, большее, чем 2. Он равен 0, 1
или -1 [6].
L(a,p) = 0, если a делится на p.
L(a,p) = 1, если a - квадратичный вычет по модулю p. L(a,p) = -1, если a не является квадратичным вычетом
по модулю p.
L(a,p) можно рассчитать следующим образом:
L(a,p = a(p-1)/2 mod p
Или можно воспользоваться следующим алгоритмом:
1.Если a = 1, то L(a,p) = 1
2.Если a четно, то L( a,p) = L(a/2,p) * 2-1)/8 3.Если a нечетно (и Ф 1), то
L(a,p)= L(p mod a, p)**(-1)(a-1)(p-1)/4
Этот метод также является эффективным способом определить, является ли a квадратичным вычетом по модулю p (для простого числа p).
Символ Якоби, J(a,n), представляет собой обобщение символа Лежандра на составные модули, он определяется для любого целого а и любого нечетного целого п. Функция удобна при проверке на простоту. Символ Якоби является функцией на множестве полученных вычетов делителей п и может быть вычислен по различным формулам.
Вот один из способов:
Определение 1: J (а,п) определен, только если п нечетно. Определение 2: J(0,«) = 0.
Определение 3: Если п - простое число, то символ Якоби J (а,п) = О, если а делится на п.
38
