Методическое пособие 145

ФГБОУ ВПО «Воронежский государственный технический университет»

Кафедра конструирования и производства радиоаппаратуры

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

ИПРОВЕРКА ГИПОТЕЗ

ОСООТВЕТСТВИИ ЭКСПЕРИМЕНТАЛЬНОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ ТЕОРЕТИЧЕСКОМУ ПРИ УПРАВЛЕНИИ КАЧЕСТВОМ В ПРИБОРОСТРОЕНИИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторной работе № 4 по дисциплине «Управление качеством в приборостроении»

по направлению подготовки бакалавров 200100.62 «Приборостроение» (профиль «Приборостроение»)

очной и заочной форм обучения

Воронеж 2013

Составители: канд. техн. наук Ю.М. Данилов, канд. физ.-мат. наук В.С. Скоробогатов

УДК 678.029.983 Законы распределения случайной величины и проверка

гипотез о соответствии экспериментального закона распределения теоретическому при управлении качеством в приборостроении: методические указания к лабораторной работе № 4 по дисциплине «Управление качеством в приборостроении» по направлению подготовки бакалавров 200100.62 «Приборостроение» (профиль «Приборостроение») очной и заочной форм обучения / ФГБОУ ВПО "Воронежский государственный технический университет"; сост. Ю.М. Данилов, В.С. Скоробогатов. Воронеж, 2013. 35 с.

В методических указаниях изложены требования и рекомендации по подготовке и выполнению лабораторной работы по изучению основных законов распределения случайной величины и методов проверки гипотезы о соответствии экспериментального закона распределения теоретическому.

Предназначены для студентов 3-4 курсов. Методические указания подготовлены в электронном ви-

де и содержатся в файле «МУлаб4» pdf.

Табл. 3. Ил. 3. Библиогр.: 3 назв.

Рецензент канд. техн. наук, доц. И.А. Новикова

Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А.В. Муратов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© ФГБОУ ВПО "Воронежский государственный технический университет", 2013

1. ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ

Целью лабораторной работы № 4 является изучение основных законов распределения случайной величины и методов проверки гипотезы о соответствии экспериментального закона распределения теоретическому.

В процессе выполнения лабораторной работы студент должен уметь практически применять полученные знания и приобретенные навыки о законах распределения случайной величины и проверке гипотез о соответствии экспериментального закона распределения теоретическому.

На выполнение лабораторной работы отводится четыре часа. Перед лабораторным занятием студент должен самостоятельно выполнить домашнее задание в соответствии с данными методическими указаниями.

Студент, явившийся на занятия, должен иметь методические указания по данной лабораторной работе, полученные в библиотеке. В начале занятия преподаватель проверяет выполнение студентом домашнего задания и наличие заготовки отчета по данной лабораторной работе в его рабочей тетради.

2. ДОМАШНЕЕ ЗАДАНИЕ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ЕГО ВЫПОЛНЕНИЮ

При выполнении домашнего задания студент должен ознакомиться с основными законами распределения случайной величины и методами проверки гипотезы о соответствии экспериментального закона распределения теоретическому. Для этого необходимо воспользоваться литературой [1, с. 3752; 2, с. 185-205], а также изучить следующий материал.

Математическое ожидание и дисперсия. Рассмотрим такое понятие в теории вероятностей как математическое ожидание. Математическое ожидание играет роль характеристики положения случайной величины в генеральной сово-

купности, и поэтому его иногда называют генеральным средним арифметическим значением случайной величины или центром группирования значений случайной величины в генеральной совокупности.

Рассмотрим случайную величину X, которая может принимать дискретные положения x1 ,х2 ,х3 ,.., хi ,.... хn с соответствующими вероятностями p1 ,р2 ,р3 ,…pi ,…,pn . Нам требуется охарактеризовать каким-то числом положение значения случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели воспользуемся формулой для средней взвешенной, где каждое значение хi при усреднении должно учитываться с «весом», пропорциональным вероятности этого значения. Тогда гене-

ральное среднее арифметическое значение случайной вели-

чины X, которое обозначим М(х), может быть подсчитано по формуле

Вычисленная выборочная средняя всегда будет содержать элемент случайности, в то время как математическое ожидание, представляющее среднее значение случайной величины в генеральной совокупности, является величиной постоянной для данной генеральной совокупности. При большом

количестве наблюдаемых значений выборочная средняя приближается к математическому ожиданию.

Дисперсию случайной величины X в генеральной совокупности, которую будем обозначать через σ2, подсчитывают по следующим формулам:

для случая, когда значения хi в генеральной совокупности не повторяются,

n 2

[M(x) xi ]

для случая, когда значения хi повторяются,

n 2

[M(x) xi ] mi

2 (x) i 1

n (2.4)

n

где n mi

i 1

Кроме характеристик положения и рассеивания нам в дальнейшем придется столкнуться с рядом характеристик, каждая из которых описывает то или иное свойство распределения. В качестве этих характеристик чаще всего применяют-

ся так называемые центральные моменты.

Практический интерес представляют второй, третий и четвертый центральные моменты. Второй центральный момент представляет собой не что иное, как дисперсию.

Третий центральный момент служит для характеристики асимметрии распределения:

n

mi (x xi )3

MЗ i 1 (2.5)

n

mi

i 1

Если распределение симметрично относительно его среднего значения, то взвешенные по соответствующим частотам кубические отклонения значений случайной величины, равноотстоящие от средней арифметической, отличаются только знаками и их сумма равна нулю. Если же распределение асимметрично, то значения параметра, лежащие по одну сторону от средней арифметической, дадут большие кубические отклонения, чем значения, лежащие по другую сторону. Знаки этих отклонений различны. Разность между суммами положительных и отрицательных слагаемых будет отличаться от нуля, являясь положительной или отрицательной. Соответственно этому знак М3 указывает на отрицательную или положительную асимметрию.

Чтобы получить меру асимметрии в виде отвлеченного числа, позвозляющего сравнивать разнородные распределения, третий момент М3 делят на куб стандартного отклонения σ3. Полученная величина, обозначаемая А, носит название

асимметрии или косости распределения:

А = М3 / σ3 (2.6)

Величина асимметрии дает нам представление о большей или меньшей асимметрии, а знак указывает на ее направление: если А>0, то средняя лежит справа от моды (правосторонняя асимметрия); если А<0, то средняя лежит слева от моды (левосторонняя асимметрия).

Кроме значения А за меру асимметрии иногда принимают число

которое часто называют коэффициентом асимметрии Особенностью симметричных рядов является равенство

трех характеристик — средней арифметической, моды и меди-

аны: x = Мо = Ме. Поэтому а для симметричных распределений равно нулю.

Четвертый центральный момент М4 служит для характеристики так называемой крутости, т. е. островершинности

или плосковершинности распределения. Это свойство распределения описывается с помощью так называемого эксцесса.

Эксцесс случайной величины X вычисляется по форму-

ле

Число 3 вычитается из отношения М4 / σ4 потому, что для весьма важного и широко распространенного в природе гауссовского закона распределения, с которым мы подробно познакомимся в дальнейшем, М4 / σ4 = 3. Поэтому для гауссовского распределения эксцесс равен нулю. Кривые, более островершинные по сравнению с ним, обладают положительным эксцессом; кривые более плосковершинные — отрицательным эксцессом.

Основные законы распределения случайной вели-

чины. В общем случае для определения вероятности того, что случайная величина X примет некоторое заранее заданное значение (или окажется меньше его), необходимо знать закон распределения случайной величины. Ввиду того что случайные величины могут быть как дискретными, так и непрерывными, распределения их вероятностей будут описываться соответственно законами распределения дискретных и непрерывных случайных величин.

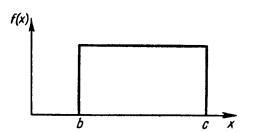
Рис. 2.1. Равновероятное (прямоугольное) распределение

Законы распределения для дискретных случайных величин, применяемые при контроле выпускаемой продукции, подробно рассмотрены в [2], поэтому в данном разделе рассмотрим законы распределения для непрерывных случайных величин, причем только те, которые необходимы для понимания последующего материала.

Равновероятный закон. Простейшим распределением для непрерывной случайной величины Х является равновероятный (равномерный, прямоугольный) закон распределения

(рис. 2.1).

Случайная величина X распределена по равновероятному закону, если плотность вероятности

Плотность вероятности f(x) иногда называют дифференциальной функцией распределения. Ее физический смысл рассмотрим несколько позже. Нетрудно убедиться в том, что площадь под кривой распределения равна единице. Действительно,

Кроме плотности вероятности для непрерывных распределений используется также интегральная функция распределения F(x), которая в общем виде выглядит следующим образом:

X

Для равновероятного закона распределения интегральная функция

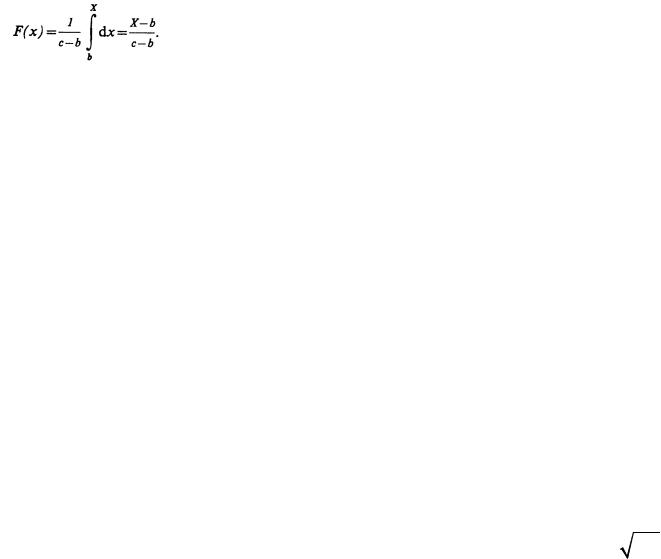
(2.12)

Физический смысл интегральной функции распределения состоит в том, что она представляет собой вероятность попадания случайной величины х в интервал от -∞ до X, где X

— определенное, наперед заданное число.

Гауссовский закон распределения. На практике часто приходится иметь дело с распределениями, которые незначительно отличаются от гауссовского. Широкое распространение гауссовского закона распределения находит теоретическое объяснение в центральной предельной теореме, смысл кото-

рой заключается в следующем. Предположим, что параметр качества Y исследуемого объекта зависит от к действующих на него независимых между собой (или слабо зависимых) факторов Х1, Х2, Х3, ..., Хк, образующих в каждый момент времени совокупность случайных независимых (или слабо зависимых) случайных величин х1, х2, х3, ..., хк, одновременно воздействующих на качество изделия. Если число этих независимых случайных величин велико (приближаясь в пределе к бесконечности) и среди них отсутствуют случайные величины с резко отличающимися от других случайных величин средними квадратичными отклонениями (или, как говорят в этом случае, отсутствуют превалирующие факторы), то в соответствии с центральной предельной теоремой распределение значений параметра качества будет стремиться к гауссовскому закону. Приэтом каждая из воздействующих на качество объекта случайных величин может подчиняться каким угодно законам распределения. Существуют три условия центральной предельной теоремы: случайные величины должны быть независимыми (или слабо зависимыми), их число должно стре-

миться к бесконечности, среди случайных величин должны отсутствовать превалирующие.

Можно утверждать, что если технологический процесс такого сложного производства, как выпуск современных ЭС, отлажен и контролируем, то распределение значений параметра качества на каждой технологической операции будет близко к гауссовскому. Это можно проверить, набрав достаточную статистику. Особенно часто встречается гауссовский закон при измерениях. Такие случайные величины, как ошибки измерений, могут быть представлены как сумма большого числа сравнительно малых слагаемых — элементарных ошибок, каждая из которых вызвана действием отдельной величины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются и сумма оказывается подчиненной закону, близкому к гауссовскому. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы все они в общей сумме равномерно играли относительно малую роль, т. е. должно выполняться третье условие центральной предельной теоремы. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму слагаемых ошибок резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.

Гауссовский закон распределения характеризуется плотностью вероятности

Для определенного распределения М(х) и σ — величины постоянные. Они являются параметрами гауссовского рас-

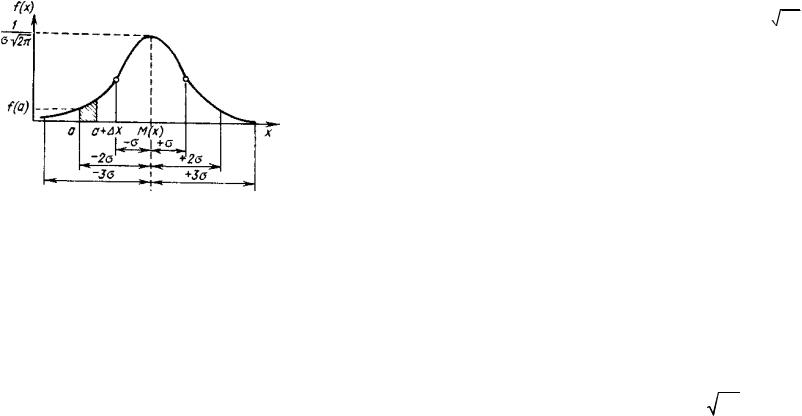
пределения. Графически функция (2.13) представлена на рис. 2.2. Поясним с помощью этого рисунка физический смысл плотности вероятности f(x). Предположим, что случайная величина х представляет собой время работы изделия до отказа (время безотказной работы). Зададимся вполне определенным значением времени отказа изделия, равным а, и поставим вопрос следующим образом: какова вероятность того, что данное изделие откажет именно в момент времени x=a?

Рис. 2.2. Кривая распределения случайной величины, подчиняющаяся гауссовскому закону

Поставленный таким образом вопрос является некорректным в теории вероятностей. И поэтому ответ будет однозначным: вероятность того, что отказ произойдет в определенный момент времени х = а, равна нулю. Если же вблизи а взять малый интервал, то вероятность того, что случайная величина х попадет в этот интервал, уже не будет равна нулю, а будет равна:

При малых Х правая часть уравнения (2.14) представляет собой площадь прямоугольника со сторонами f( а) и Х. Если обе части уравнения (2.14) разделить на Х, то получим вероятность, приходящуюся на единицу длины, т. е. плотность

вероятности (аналогично тому, что плотность вещества — это масса на единицу объема)

в этом и заключается физический смысл плотности вероятности.

Вернемся опять к кривой гауссовского закона распределения, приведенной на рис. 2.2. Как видно, кривая распределения имеет характерную колоколообразную форму. Макси-

мальная ордината кривой, равная 1/ 2 , соответствует

точке х=М(х)—центру распределения. Точка перегиба кривой располагается на расстоянии ±σ от центра распределения (как показано на рис. 2.2). По мере удаления от точки М(х) плотность распределения уменьшается, и при х→±∞ кривая асимптотически приближается к оси абсцисс.

Если при изменении центра группировки М(х) кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы, то при изменении σ кривая распределения меняет свою форму.

Максимальная ордината кривой распределения обратно пропорциональна σ. Так как площадь под кривой всегда должна оставаться равной единице, то при увеличении σ кривая опускается вниз, одновременно растягиваясь вдоль оси абсцисс. Напротив, при уменьшении σ кривая вытягивается вверх, одновременно сжимаясь с боков.

Если рассмотреть частный случай, когда М(х) равно нулю, а σ равно единице, то, обозначив плотность вероятности через f0(x), уравнение (2.13) можно записать в следующем виде:

Функция (2.14) легко табулируется и для нее не представляет труда составить таблицы. С помощью таблицы для

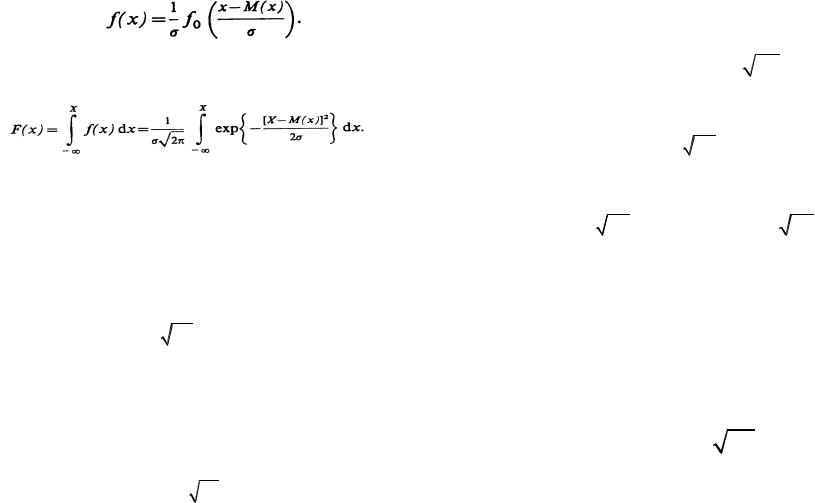
f0 (х) нетрудно вычислить f(x), когда σ не равна единице, а М(х) отлично от нуля. Действительно, из (2.11) и (2.14) имеем

(2.17)

Интегральная функция распределения для случая гауссовского закона

(2.18)

С помощью формулы (2.18) определяется вероятность того, что случайная величина х будет меньше некоторого значения X. Если же требуется найти вероятность того, что случайная величина х, имеющая гауссовский закон распределения, будет лежать в каких-либо пределах от х1 до х2, необходимо соответственно изменить пределы интегрирования в выражении (2.18), т. е.

Произведя в (2.19) замену переменной интегрирования X на α=[X—M(x)]/σ, которую называют нормированием, и учитывая, что Х= ασ ± М(х), а dx = σdα, получаем

Новые нормированные пределы интегрирования α1 и α2 заменили пределы х1 и х2. Представив правую часть выражения (2.20) в виде суммы двух интегралов, получим

Знак перед первым слагаемым изменился вследствие изменения пределов интегрирования α1 - 0на 0 – α2.

Функция

называется нормированной функцией Лапласа или интегралом вероятности. Для этой функции имеется в Приложении табл. П1. Таблица построена для положительных значений, но, учитывая, что функция Ф(α) нечетная, т. е. Ф(-α)= -Ф(α), для от-

рицательных значений α табличный результат следует брать со знаком минус. В некоторых случаях следует брать функцию

Ф1(α)=2Ф(α). (2.22)

Таким образом, для получения Ф1(α) достаточно удвоить значение Ф(α), взятое из табл. П.1 Приложения.

Площадь под кривой Гаусса равна 1, или 100% всех значений случайной величины в генеральной совокупности. Величина площади, заключенной между одно-, двух- и трехсигмовыми границами, найденными при подстановке в (2.22) значений Ф(а), взятых из табл. П.1 Приложения для σ, соответственно равного 1, 2 и 3, приведена табл. 2.1.

Таблица 2.1

Величина площади под кривой Гаусса при различных границах изменения случайной величины

Приведенные в табл. 2.1 данные можно истолковать следующим образом. Если 68,27%, т. е. 2/3, наблюдаемых значений случайной величины лежит между границами М(х) — σ и М(х) + σ , то 31,73% всех наблюдений следует ожидать за этими границами (соответствующими точками перегиба кривой Гаусса), а именно: 15,865% — за границей М(х)— σ; 15,865% — за границей М(х)+ σ в силу симметричности гауссовского распределения. Как уже отмечалось ранее, односигмовые границы соответствуют точкам перегиба кривой Гаусса.

Между трехсигмовыми границами [М(х) - 3σ; М(х) + 3σ] находится 99,73% всех наблюдений, т. е. практически все значения. Только 0,27% значений лежит за этими границами, а именно 0,135% — за границей М (х) -Зσ; 0,135% — за границей М(х) + Зσ. Это означает, что при проведении 10 000 наблюдений в среднем 27 наблюдений будет лежать за трехсигмовыми границами или при 270 наблюдениях — одно. Поэтому, зная стандартное отклонение и математическое ожидание случайной величины, подчиняющейся гауссовскому закону распределения, можно ориентировочно указать интервал ее практически возможных минимальных и максимальных значений. И если какое-либо значение появляется за пределами трехсигмового участка, то его можно считать чисто случайным. Так как вероятность появления такого события очень мала, а именно 1/270, следует считать, что рассматриваемое событие является практически невозможным. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием правила

трех сигм.

На практике участок, лежащий внутри трехсигмовых границ, называют областью статистического допуска параметра качества соответствующего изделия или процесса его изготовления.

Таким образом, следует отметить, что если распределение значений параметра качества близко к гауссовскому, то это означает, что технологический процесс отлажен и контролируем. Поэтому часто приходится использовать различные критерии для проверки соответствия экспериментального (т.е. полученного при измерении параметра качества изделий в выборке) закона распределения случайной величины гауссовскому.

Статистическая проверка гипотез. Критерий Пир-

сона. Для проверки гипотезы о соответствии экспериментального закона распределения случайной величины

теоретическому наиболее часто применяют критерий Пирсона или, как его иначе называют, критерий χ2 («хи-квадрат»), так как принятие и отклонение гипотезы основаны на χ - распределении.

Предположим, что имеется статистический ряд наблюдений над случайной величиной X. Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина имеет предполагаемый закон распределения, заданный интегральной функцией распределения F(x) или плотностью вероятностей f(x), который в дальнейшем будем называть теоретическим законом распределения.

Первоначально статистический ряд разбивают на k интервалов и подсчитывают число значений случайной величины X в каждом интервале. В результате получают экспериментальный ряд частот:

m1' , m2' , m3' , , mk'

Следует сразу оговорить, что предпосылкой применения критерия χ2 является достаточная заполненность интервалов частотами. На практике рекомендуется иметь в каждом интервале не менее 5-10 наблюдений. Если число наблюдений в отдельных интервалах мало, имеет смысл объединить эти интервалы.

Исходя из предполагаемого теоретического закона распределения вычисляют частоты тi в тех самых интервалах, на которые разбит статистический ряд. В результате получают теоретический ряд частот в k интервалах m1 ,m2, т3 ,..., mк.

Для проверки согласованности теоретического и экспериментального распределения подсчитывают меру расхождения:

или

и число степеней свободы ν. Число степеней свободы равно в этом случае числу интервалов k минус число ограничений f:

Число ограничений равно числу параметров в рассматриваемом законе распределения, увеличенному на единицу. Например, для гауссовского закона имеется два параметра: [М(х) и σ ] в этом случае число ограничений равно трем.

Для распределения χ2 составлены специальные таблицы (см. табл. П2 Приложения ). Пользуясь этими таблицами, можно для каждого значения χ 2 и числа степеней свободы v определить вероятность Р того, что за счет чисто случайных причин мера расхождения теоретического и экспериментального распределений (2.23) будет меньше, чем фактически наблюдаемое в данной серии опытов значение χ2. Если эта вероятность Р мала (настолько, что событие с такой вероятностью можно считать практически невозможным), то результат опыта следует считать противоречащим гипотезе о том, что закон распределения величины X есть F(х). Эту гипотезу следует отбросить как неправдоподобную.

Напротив, если вероятность Р сравнительно велика, можно признать расхождение между теоретическим и экспериментальным распределениями несущественным и отнести его за счет случайных причин. Гипотезу о том, что величина X распределена по закону F(x), можно считать в этом случае правдоподобной, по крайней мере не противоречащей полученным, экспериментальным данным.