Общие сведения

Электронный осциллограф – универсальный измерительный прибор, применяемый для визуального наблюдения и фотографирования электрических сигналов и измерения их параметров.

Принцип действия электронного осциллографа состоит в следующем. Сфокусированный электронный луч. Проходя между горизонтально и вертикально отклоняющими пластинами Х и Y, может отклоняться под действием напряжения, приложенного к пластинам перпендикулярно плоскости пластин. Попадая на экран, луч оставляет светящееся пятно, которое, перемещаясь по экрану в соответствии с законом подаваемого на пластины Х и Y напряжения, формирует изображение.

В том случае, когда напряжение на горизонтально отклоняющих пластинах линейно изменяется в течение определенного промежутка времени (периода развертки Т_р), говорят, что осциллограф работает в режиме «линейной развертки». При этом на экране наблюдается изображение, соответствующее форме напряжения, подаваемого на вертикальные пластины. Однако изображение будет устойчивым только в том случае, если период горизонтальной развертки (Т_р) и период сигнала (Т_с), отклоняющего луч в вертикальном направлении, являются кратными друг дугу, т.е. Т_р = п×Т_с, где п = 1, 2, 3, …, рис. 3.1.

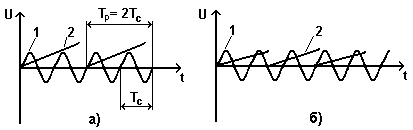
Рис. 3.1. Временные зависимости напряжений сигнала

и развертки: а – Т_р = п×Т_с (п = 2); б – Т_р ¹ п×Т_с

Кратность Т_р и Т_с достигается либо введением синхронизации от внешнего источника (внешняя синхронизация), либо самим напряжением сигнала (внутренняя синхронизация). Отметим, что в процессе синхронизации изменяется только период Т_р, а скорость развертки остается неизменной величиной, задаваемой дискретно переключателем «ВРЕМЯ РАЗВЕРТКИ», проградуированным в единицах времени (t) «пробега» лучом «ЕДИНИЦЫ ДЛИНЫ» экрана (обычно 1 см). Данным обстоятельством пользуются для определения периода Т и частоты f исследуемого сигнала

Т = l×t ; f = 1/T = 1/l×t , (3.1)

где l – расстояние между двумя эквивалентными точками изображения периодического сигнала. Таким же образом проводят измерения других временных и динамических характеристик сигнала (например, длительности импульса, скорости нарастания или спада напряжения и т.д.).

Кроме линейной, на практике часто используют синусоидальную развертку. Она реализуется, когда на Х и Y пластины подаются синусоидальные напряжения с частотами f₁ и f₂ соответственно:

;

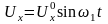и (3.2)

,

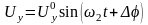где 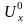и 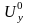– амплитуды напряжений, подаваемых на Х и Y пластины осциллографа; Dj – сдвиг фаз между U_x и U_y, имеющий смысл в том случае, когда w = 2pf.

Координаты луча (Х, Y) на экране связаны с U_x и U_y через соответствующие коэффициенты чувствительности К_х и К_у (Х = U_xК_х и Y = U_yК_у) каналов осциллографа. Учитывая это и преобразуя уравнение (3.2) для случая 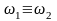, можно получить выражение, описывающее траекторию луча:

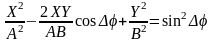, (3.3)

которое является уравнением эллипса, рис. 3.2 (А и В – максимальные значения отклонений луча в горизонтальном и вертикальном направлениях).

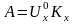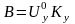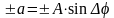Очевидно, что максимальное отклонение луча по горизонтали , а по вертикали . В моменты времени, определяемые условиями w×t = p×n и w×t = p×(1/2 + n), где п = 1, 2, … , луч пересекает координатные оси Х и Y в точках и 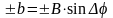(рис 3.2).

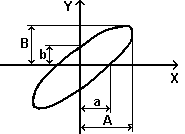
Рис. 3.2. Траектория луча осциллографа

Этим обстоятельством пользуются на практике для определения сдвига фаз между напряжениями, подаваемыми на Х и Y каналы осциллографа:

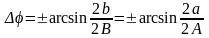. (3.4)

Синусоидальную развертку можно также использовать для определения неизвестной частоты f_x путем сравнения ее с эталонной частотой f₀ образцового генератора. Практическое применение нашли метод фигур Лиссажу и метод меток.

Измерение f с помощью фигур Лиссажу заключается в том, что на входы Х и Y отклоняющих систем подается напряжение измеряемой f_x и образцовой f₀ частот. При этом на экране осциллографа наблюдается фигура, которая остается неподвижной, если отношение частот равно отношению целых чисел: f_x/f₀ или f₀/f_x = п. Частный случай п = 1 подробно рассмотрен выше).

Для нахождения отношения частот f_x/f₀ (рис. 3.3) необходимо условно провести горизонтальную и вертикальную линии, которые пересекали бы фигуру, но не проходили через ее узлы. Число горизонтальных п_г и число вертикальных п_в пересечений находятся в соотношении п_г/п_в = f_x/f₀, откуда

f_x = f_0×(п_г/п_в). (3.5)

Для фигуры, приведенной на рис. 3.3, f_x = 2f₀.

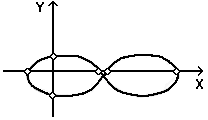
Рис. 3.3. Изображение фигуры Лиссажу