Примеры решения задач к контрольной работе

Пример 1. Решить систему линейных алгебраических уравнений методом Жордана-Гаусса.

Решение. Запишем коэффициенты, свободные члены и суммы коэффициентов и свободных членов ( —контрольный столбец, в котором содержатся суммы элементов соответствующих строк,) в следующую таблицу:

x	y	z	t	b
1	1	-3	2	6	7
1	-2	0	-1	-6	-8
	1	1	3	16	21
2	-3	2	0	6	7

Преобразование Жордана системы уравнений позволяет перейти к другой системе, равносильной (имеющей то же решение) исходной. Соответствующая первому шагу преобразования таблица заполняется таким образом. Выбираем в качестве разрешающего элемента коэффициент при х в первом уравнении. Перепишем без изменения разрешающую строку таблицы, содержащую разрешающий элемент, а все элементы 1-го столбца, кроме разрешающего, заменим нулями:

x	y	z	t	b
1	1	-3	2	6	7
0
0
0

Далее применяем правило прямоугольника для заполнения пустых клеток таблицы (это же правило применяем и к контрольному столбцу). Правило прямоугольника связано с формулой пересчета элементов матрицы новой системы, не принадлежащих разрешающей строке (она не меняется, если разрешающий элемент преобразован к единице) и разрешающему столбцу (он содержит нули кроме разрешающего элемента). Формула пересчета имеет вид:

,

где - разрешающий элемент. Для нахождения элемента следует из элемента вычесть произведение элементов и ; расположенных в противоположных вершинах прямоугольника, деленное на разрешающий элемент (см. Рис.1).

В результате пересчета получаем таблицу:

x	y	z	t	b
1	1	-3	2	6	7
0	-3	3	-3	-12	-15
0	1	1	3	16	21
0	-5	8	-4	-6	-7

Разделим элементы второй строки на -3 и примем за разрешающий 2-й элемент 2-й строки. 1-д столбец перепишем без изменения, элементы 2-го столбца, кроме разрешающего, заменим нулями, 2-ю (разрешающую) строку перепишем без изменения, элементы остальных клеток таблицы преобразуем по правилу прямоугольника:

x	y	z	t	b
1	0	-2	1	2	2
0	1	-1	1	4	5
0	0	2	2	12	16
0	0	3	1	14	18

Разделим элементы третьей строки на 2.

x	y	z	t	b
1	0	-2	1	2	2
0	1	-1	1	4	5
0	0	1	1	6	8
0	0	3	1	14	18

Преобразуем таблицу, приняв за разрешающий 3-й элемент 3-го столбца:

x	y	z	t	b
1	0	0	3	1	18
0	1	0	2	10	13
0	0	1	1	6	8
0	0	0	-2	-4	-6

Разделим элементы четверной сроки на -2, чтобы сформировать новый разрешающий элемент :

x	y	z	t	b
1	0	0	3	1	18
0	1	0	2	10	13
0	0	1	1	6	8
0	0	0	1	2	3

Используя вновь полученный разрешающий элемент, имеем:

x	y	z	t	b
1	0	0	0	8	9
0	1	0	0	6	7
0	0	1	0	4	5
0	0	0	1	2	3

Таблица соответствует системе уравнений

Решение системы: , , , .

Пример №2. Решить задачу линейного программирования графическим методом.

Решение. Сначала находится многоугольник решений – область на координатной плоскости, удовлетворяющую всем ограничениям задачи. Построим прямые, уравнения которых получаются в результате замены в системе ограничений знаков неравенств на знаки точных равенств. Получаем уравнения прямых линий на плоскости. Для построения прямых находятся координаты двух точек пересечения с осями координат. Для линии , соответствующей первому неравенству получаем координаты точек пересечения с осями: (0;5) и (-2,5;0). Для того, чтобы определить, с какой стороны от проведенной линии находится полуплоскость, удовлетворяющая неравенству, необходимо подставить в неравенство координаты начала координат (0;0). Если получается верное неравенство, то точка начала координат принадлежит искомой полуплоскости, в случае получения неверного соотношения выбирается другая полуплоскость. Для прямой получаем координаты точек пересечения с осями: (0;7) и (7;0). Для прямой получаем координаты точек пересечения с осями: (0;- ) и (1;0).

Далее получим многоугольник решений ОАВСD. Построим вектор-нормаль, выходящий из начала координат в направлении точки с координатами – коэффициентами функции цели ( , ) или пропорциональными этим координатам (Х₁ = 1, Х₂ = 0,5). Линия уровня строится перпендикулярно вектору-нормали. Передвигаем линию уровня в направлении, указанном вектором нормали. В результате находим точку В, в которой целевая функция принимает максимальное значение. Находим координаты этой точки. Для этого решим систему уравнений, которые соответствуют прямым, на пересечении которых находится точка В:

Решая систему уравнений, получаем , .

Вычислим значение функции цели в точке :

=13,333.

Пример № 3. Сформулировать и решить задачу линейного программирования симплекс-методом. Предприятие выпускает три вида изделий ( , , ), используя три вида ресурсов ( , , ). Запасы ресурсов ограничены (указаны в последнем столбце). Прибыль от реализации единицы изделия (последняя строка) и нормы расхода ресурсов представлены в таблицах. Определить ассортимент и объемы выпуска продукции, получаемую прибыль, величину остатков ресурсов. Найти решение задачи симплексным методом с представлением всех симплексных таблиц (промежуточных шагов решения) и проанализировать полученные результаты. Составить двойственную задачу. Определить двойственные оценки из последней симплексной таблицы и провести анализ последней симплексной таблицы.

				Запас ресурсов
	4	2	1	180
	3	1	3	210
	1	2	5	244
Прибыль	10	14	12

Решение. Обозначим через – количество изделий вида , которое должно выпустить предприятие; – количество изделий вида , – количество изделий вида . Нормы расхода ресурсов на производство единиц продукции описывается матрицей условий

,

Далее записываем систему неравенств, связанных с ограниченностью ресурсов:

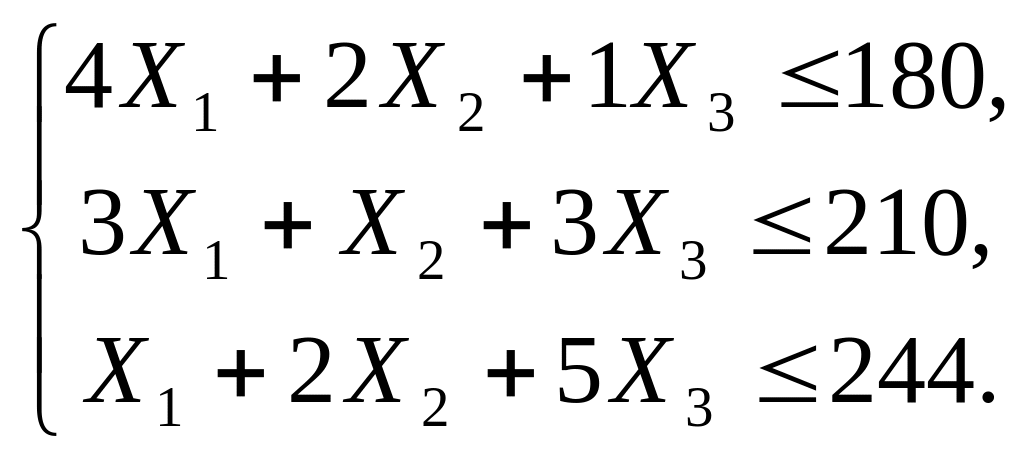
Целевая функция составляется с использованием прибылей . Доход за месяц должен быть максимизирован:

 max.

Выпускается только выгодная продукция (в этом случае > 0), а невыгодная не производится (тогда = 0), т.е. добавляются неравенства

 0,  0,  0.

По условиям задания сформулируем стандартную задачу линейного программирования:

,

Для записи задачи в канонической форме приведем ограничения – неравенства к системе уравнений. Приравняем левые и правые части ограничений путем введения дополнительных переменных.

Исходные переменные , и принимаем в качестве небазисных (свободных), а дополнительные , и считаем базисными и составляем симплекс-таблицу:

Базис		Свободн. члены	10	14	12	0	0	0
	0	180	4	2	1	1	0	0	90
	0	210	3	1	3	0	1	0	210
	0	244	1	2	5	0	0	1	122
			-10	-14	-12	0	0	0

Сначала небазисные переменные полагаются равными нулю, а базисные переменные берутся равными свободным членам (первый опорный план: (0,0,0,180,210,244)). Второй столбец содержит коэффициенты при базисных неизвестных целевой функции. Последняя строка (дельта-строка) заполнена симплексными разностями или симплексными оценками неизвестных, вычисляемыми по формуле

_j = ,

где .

Симплексные оценки неизвестных позволяют ввести простой критерий оптимальности очередного базисного плана: если все симплексные оценки неотрицательны, то этот план оптимален.

Вычисляем симплексные оценки:

,

,

,

,

,

.

Так как среди оценок _j есть отрицательные, то опорный план не является оптимальным и значение целевой функции можно улучшить. Для этого нужно пересчитать симплексную таблицу, выбрав соответствующим образом разрешающий (ключевой) элемент, стоящий на пересечении разрешающей (ключевой) строки и разрешающего (ключевого) столбца, причем берется столбец с наибольшей по абсолютной величине отрицательной оценкой, т.е. второй столбец.

Для определения разрешающей строки находим отношения правых частей уравнений (свободных членов) к положительным элементам ключевого столбца:

(min),

Полученные значения симплексного отношения  записываются в последний столбец симплексной таблицы. Из них выбирается наименьшая величина, которая указывает на ключевую строку (первую строку). Разрешающим элементом оказалась выделенная жирным шрифтом «двойка».

Далее, делим элементы разрешающей строки на разрешающий элемент . С помощью метода Жордана - Гаусса проводят пересчет таблицы таким образом, чтобы элементы ключевого столбца имели единицу на месте ключевого элемента и нули на месте всех остальных элементов. Для этого вычтем из элементов третьей строки соответствующие элементы первой строки, а из элементов второй строки – элементы первой строки, поделенные на два (на ключевой элемент).

Переменная, соответствующая ключевой строке, выводится из базиса, а переменная, соответствующая ключевому столбцу, вводится вместо нее в базис

Базис		Свободн. члены	10	14	12	0	0	0
	14	90	2	1	1/2	1/2	0	0	180
	0	120	1	0	5/2	-1/2	1	0	48
	0	64	-3	0	4	-1	0	1	16
			18	0	-5	7	0	0

Вычисляем симплексные оценки и симплексные отношения:

,

,

,

,

,

, , 64/4 (min).

Следующая итерация связана с выбором разрешающего столбца с и разрешающей строки с , т. е. разрешающим элементом является 4, а базисная неизвестная меняется на . Симплекс-таблица, соответствующая такой замене, имеет вид:

Базис		Свободн. члены	10	14	12	0	0	0
	14	82	19/8	1	0	5/8	0	-1/8
	0	80	23/8	0	0	1/8	1	-5/8
	12	16	-3/4	0	1	-1/4	0	1/4
			57/4	0	0	23/4	0	5/4

Поскольку все оценки положительные, то данный план является оптимальным. При оптимальном плане следует выпускать изделий вида в количестве 82 штук, изделий – 16 штук. 80 кг сырья вида остаются неиспользованными, а общий доход от продажи изделий составит

1340 ден.ед.

Оптимальным решением двойственной задачи является Y* = (23/4, 0, 5/4), поскольку решение двойственной задачи находится в столбцах, соответствующих дополнительным переменным исходной задачи , и .

Переменные и обозначают условные двойственные оценки единицы сырья первого и третьего вида. Они отличны от нуля, и сырье этих видов и полностью использовано при оптимальном плане производства. Следует отметить, что чем больше двойственные оценки, тем дефицитнее сырье. Переменная = 0, и второй вид сырья полностью не используется.

Двойственные оценки показывают, насколько возрастет оптимальное (максимальное) значение функции цели прямой задачи при увеличении количества сырья соответствующего вида на 1 кг. Например, увеличение количества сырья на 1 кг приведет к новому оптимальному плану производства изделий, при котором доход возрастет на 23/4 = 5,75 и станет равным 1345,75 ден.ед, а числа, стоящие в столбце последней симплексной таблицы, покажут, что это может быть достигнуто за счет увеличения выпуска изделий на 5/8 единиц и выпуска изделий на 1/4 единицы. Использование сырья вида уменьшится при этом на 1/8 кг.

Увеличение на 1 кг сырья дает новый оптимальный план, при котором доход возрастет на 5/4 = 1,25 ден.ед. и составит 1341,25 ден.ед. Это будет достигнуто за счет увеличения выпуска изделия на 1/4 единицы и уменьшения выпуска изделия на 1/8 единицы, причем объем используемого сырья второго вида возрастет на 5/8 кг.

Минимальное значение целевой функции двойственной задачи:

F(y) = 180  23/4 + 210  0 + 244  5/4 = 1340

совпадает с максимальным значением целевой функции исходной задачи.

Пример № 4. По заданной матрице межпроизводственных связей и заданному вектору валового продукта найти конечный продукт и чистый продукт каждой отрасли. На будущий период для полученной при решении задачи (старой) матрицы прямых затрат и нового вектора конечного продукта рассчитать требуемый вектор валового продукта.

, , .

Решение. Для составления балансовой таблицы необходимо определить конечный продукт и чистый продукт каждой отрасли по формулам:

.

, .

Отрасль	Потребление отраслей			Конечный продукт	Валовый продукт
	1	2	3
1	10	9	11	6	36
2	9	18	12	9	48
3	11	16	12	5	44
Чистый продукт	6	5	9	20=20	128

Получим матрицу прямых затрат :

.

Вычислим матрицу :

.

Валовый продукт, соответствующий новой матрице-столбцу (вектору) конечного продукта находится по формуле .

Вычислим элементы обратной матрицы, предварительно посчитав определитель и присоединенную матрицу (матрицу алгебраических дополнений),

.

,

,

,

,

,

,

,

,

.

.