14.2.Особенности расчета и конструкции косозубых и шевронных зубчатых колес

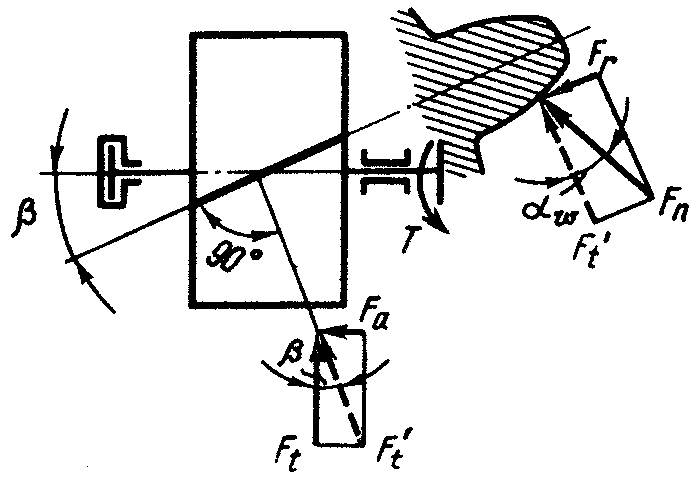
Рис. 14.77. Схема сил, возникающих в косозубом зацеплении

Если прямозубые цилиндрические колеса применяют преимущественно при невысоких и средних окружных скоростях (5–20 м/с), в планетарных, открытых передачах, а также при необходимости осевого перемещения колес для переключения скоростей (коробки передач), то косозубые колеса применяют для ответственных передач, при средних и высоких скоростях (8–30 м/с). Объем использования косозубых колес составляет 30% от всех цилиндрических колес в машиностроении и непрерывно возрастает.

В отличие от прямозубых, косозубые передачи должны проектироваться так, чтобы в зацеплении находилось постоянно минимум две пары зубьев. Для этого необходимо, чтобы этого ширина колес (b) была больше осевого шага (t₀). При несоблюдении этого условия передача будет работать, как прямозубая.

При значительной ширине колеса и большом угле наклона зубьев в зацеплении может одновременно до десяти и больше пар зубьев. Зубья косозубых передач входят в зацепление постепенно: контакт начинается в точке по мере поворота колес контактная линия растет, некоторое время остается постоянной длины и далее постепенно сокращается до нуля. На боковых поверхностях зубьев контактные линии занимают наклонное положение.

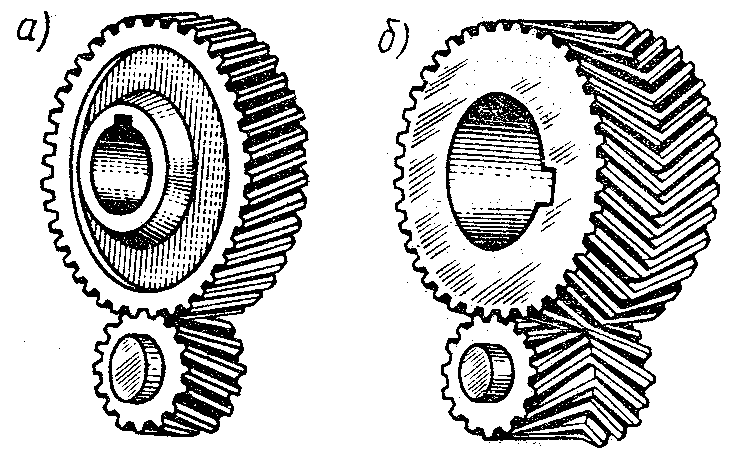
Рис. 14.78. Цилиндрические колеса:

а) косозубые; б) шевронные

В большинстве конструкций угол наклона зубьев “β ” принимают от 8˚ до 18˚ (редко до 25˚) с тем, чтобы обеспечить осевой коэффициент перекрытия в пределах не менее 1,1-1,2.

Точное значение угла “β ” выбирают таким, чтобы при стандартных значениях нормальных модулей межосевое расстояние “a_w” соответствовало стандартам.

Работа косозубой передачи связана с действием на опоры осевых нагрузок, поэтому в мощных редукторах применяют передачи, не передающие на опоры осевых нагрузок. Шевронные колеса представляют собой соединенные вместе два косозубых колеса с одинаковым, но противоположно направленным наклоном зубьев, и имеют угол наклона зубьев в пределах β = 25–40.

По форме расчета на прочность косозубых и шевронных колес аналогичен расчету цилиндрических колес, однако имеет свои особенности.

Расчеты на изгиб. Косые и шевронные зубья значительно (примерно на 30%) прочнее прямых ввиду того, что:

• в зацеплении участвуют несколько пар зубьев , что учитывается коэффициентом К_α;

- контактная линия наклонена к основанию зуба, а сам зуб работает не как балка, а как пластина, что учитывается коэффициентом Y_β;

• в опасном сечении зуб утолщен (другой коэффициент прочности зуба по местным напряжениям Y_K).

Коэффициент K принимают в зависимости от степени точности передачи (K_α > 1,0). При β ≤ 40 коэффициент (Y_β < 1,0) Коэффициент Y_F принимают в зависимости от эквивалентного числа зубьев Z_V по таблицам для цилиндрических прямозубых колес.

Эквивалентное число зубьев Z_V – это число зубьев эквивалентной прямозубой шестерни, имеющей радиус делительной окружности равный радиусу кривизны длительного цилиндра в сечении, нормальном к зубу. Если прочность на изгиб является основным критерием, то нормальный модуль определяется по формуле:

;

где: .

Если модуль определяется по заданному межосевому расстоянию (когда основным критерием является контактная прочность), то: