
- •Введение
- •Основные задачи математической статистики
- •2. Генеральная совокупность, выборка
- •3. Статистический ряд. Гистограмма
- •Коэффициенты соотношений заемных и собственных средств предприятий
- •Сгруппированный ряд наблюдений
- •Числовые характеристики статистического распределения. Обработка опытов
- •5. Доверительный интервал. Доверительная вероятность
- •Методы расчета сводных характеристик выборки
- •7. Проверка статистических гипотез
- •8. Сравнение двух дисперсий нормальных генеральных совокупностей
- •9. Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности
- •10. Выравнивание статистических рядов
- •11. Критерии согласия
- •12. Методика вычисления теоретических частот нормального распределения
- •13. Система двух случайных величин
- •13.1. Понятие о системе нескольких случайных величин
- •13.2. Закон распределения вероятностей дискретной двумерной случайной величины
- •13.3. Вероятность попадания случайной точки в полуполосу
- •13.4. Вероятность попадания случайной точки в прямоугольник
- •13.5. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности)
- •13.6. Условные законы распределения составляющих системы дискретных случайных величин
- •13.7. Условное математическое ожидание
- •13.8. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции
- •13.9. Линейная регрессия. Прямые линии среднеквадратической регрессии
- •14. Элементы теории корреляции
- •14.1. Отыскание параметров выборочного уравнения прямой линии среднеквадратической регрессии по несгруппированным данным
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Критические точки распределения
- •Библиографический список
- •Подписано к изданию 20.11.2007 .
- •394026 Воронеж, Московский просп., 14
5. Доверительный интервал. Доверительная вероятность
Ранее был рассмотрен
вопрос об оценке неизвестного параметра
одним числом.
Такая оценка называется «точечной».
Однако в ряде задач требуется не только
найти для параметра
подходящее численное значение, но и
оценить его точность и надежность.
Требуется знать, к каким ошибкам может
привести замена параметра
его точечной оценкой
![]() ,
и с какой
степенью уверенности можно ожидать,
что эти ошибки не выйдут за известные
пределы?
,
и с какой
степенью уверенности можно ожидать,
что эти ошибки не выйдут за известные
пределы?
Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка в значительной мере случайна и приближенная замена на может привести к серьезным ошибкам.
Чтобы дать представление о точности и надежности оценки , в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями.
При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, то есть приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная
по данным выборки статистическая
характеристика
служит оценкой неизвестного параметра
.
Ясно, что
тем точнее определяет параметр
,
чем меньше абсолютная величина разности
![]() .
Другими словами, если
<
.
Другими словами, если
<![]() ,
то чем меньше
,
тем оценка точнее. Таким образом,
положительное число
характеризует точность оценки.
,
то чем меньше
,
тем оценка точнее. Таким образом,
положительное число
характеризует точность оценки.
Однако статистические
методы не позволяют категорически
утверждать, что оценка
![]() удовлетворяет неравенству
<
;
можно лишь говорить о вероятности
удовлетворяет неравенству
<
;
можно лишь говорить о вероятности
![]() ,
с которой это неравенство осуществляется.
,
с которой это неравенство осуществляется.
Надежностью
(доверительной вероятностью) оценки
по
называют вероятность
,
с которой осуществляется
<
.
Обычно надежность оценки задается
наперед, при чем в качестве
берут число, близкое к единице. Наиболее
часто задают надежность, равную 0,95; 0,99
и 0,999. Пусть вероятность того, что
<
,
равна
:
![]() Заменив неравенство
<
равносильным ему двойным неравенством
Заменив неравенство
<
равносильным ему двойным неравенством
![]() ,
или
,
или
![]() ,
имеем
,
имеем
![]() .
.
Вероятность того,
что интервал
![]() заключает в себе (покрывает) неизвестный
параметр
,
равна
.
заключает в себе (покрывает) неизвестный
параметр
,
равна
.
Доверительным называют интервал , который покрывает неизвестный параметр с заданной надежностью .
Тогда диапазон
практически возможных значений ошибки,
возникающей при замене
на
,
будет
![]() ,
а большие по величине ошибки будут
появляться лишь с малой вероятностью
,
а большие по величине ошибки будут
появляться лишь с малой вероятностью
![]() ,
а неизвестное значение параметра
попадает
в интервал
,
а неизвестное значение параметра
попадает
в интервал
![]() .
.
Величина
![]() рассматривается не как вероятность
«попадания» точки в интервал
рассматривается не как вероятность
«попадания» точки в интервал
![]() ,
а как вероятность того, что случайный
интервал
,
а как вероятность того, что случайный
интервал
![]() накроет точку
(рис. 2).
накроет точку
(рис. 2).

Вероятность
называют доверительной
вероятностью,
а интервал
- доверительным
интервалом.
Границы интервала
:
![]() и
и
![]() называются доверительными
границами.
называются доверительными
границами.
Пусть произведено n независимых опытов над случайной величиной Х, характеристики которой – математическое ожидание m и дисперсия D – неизвестны. Для этих параметров получены оценки:
 ;
;
 .
.
Требуется построить доверительный интервал , соответствующий доверительной вероятности (заданной), для математического ожидания m и дисперсии D величины Х.
Исходим из того,
что величины
и
распределены по нормальному закону.
Характеристики этого закона –
математическое ожидание и дисперсия –
равны соответственно а
и
![]() .
Предположим, что дисперсия
D
известна.
Найдем такую величину
,
для которой
.
Предположим, что дисперсия
D
известна.
Найдем такую величину
,
для которой
![]() .
.
Используем формулу для вычисления вероятности заданного отклонения
![]() ,
,
а именно
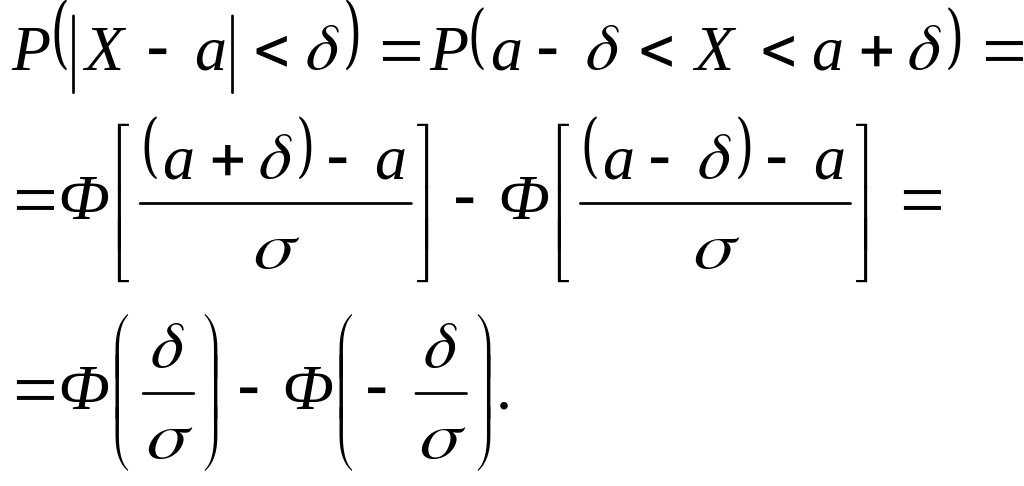
Приняв
во внимание тот факт, что функция Лапласа
– нечетная, имеем
![]()
Заменив
X
на
![]() ,
а
,
а
![]() на
на
![]() ,
получим
,
получим
![]() ,
,
где
![]() - среднее квадратическое отклонение
оценки
,
- среднее квадратическое отклонение
оценки
,
![]() .
.
Отсюда
![]() ,
а, приняв во внимание, что вероятность
Р
задана и равна
,
то окончательно имеем
,
а, приняв во внимание, что вероятность
Р
задана и равна
,
то окончательно имеем
![]() .
.
Таким образом, с
вероятностью
(надежностью) можно утверждать, что
доверительный интервал
![]() =
=![]() покрывает неизвестный параметр а;
точность оценки
покрывает неизвестный параметр а;
точность оценки
![]() .
Число t
определяется из равенства
.
Число t
определяется из равенства
![]() или
или
![]() .
По таблице функции Лапласа (табл. 1
приложения) находят аргумент t,
которому соответствует значение функции
Лапласа, равное
.
По таблице функции Лапласа (табл. 1
приложения) находят аргумент t,
которому соответствует значение функции
Лапласа, равное
![]() .
.
Пример.
Случайная величина X
имеет
нормальное распределение с известным
средним квадратическим отклонением
![]() .
Найти доверительные интервалы для
оценки неизвестного математического
ожидания a
по выборочным средним
.
Найти доверительные интервалы для
оценки неизвестного математического
ожидания a
по выборочным средним
![]() ,
если объем выборки n=36
и задана надежность оценки
,
если объем выборки n=36
и задана надежность оценки
![]() .
.
Решение.
Найдем t.
Из соотношения
![]() получим
получим
![]() По таблице функции Лапласа находим
t=1,96.
По таблице функции Лапласа находим
t=1,96.
Найдем точность оценки:
=![]()
Доверительный
интервал таков:
![]() .
.
Поясним смысл, который имеет заданная надежность. Надежность указывает, что если произведено достаточное большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала.
Предположим теперь, что дисперсия D неизвестна.
Тогда доверительный интервал для математического ожидания находится
![]() =
=![]() ,
,
где
величина
![]() определяется из условия
определяется из условия
![]()
и находится из таблицы распределения Стьюдента (табл. 2 приложения).
Здесь
![]() плотность закона распределения Стьюдента
с n-1
степенями свободы
плотность закона распределения Стьюдента
с n-1
степенями свободы
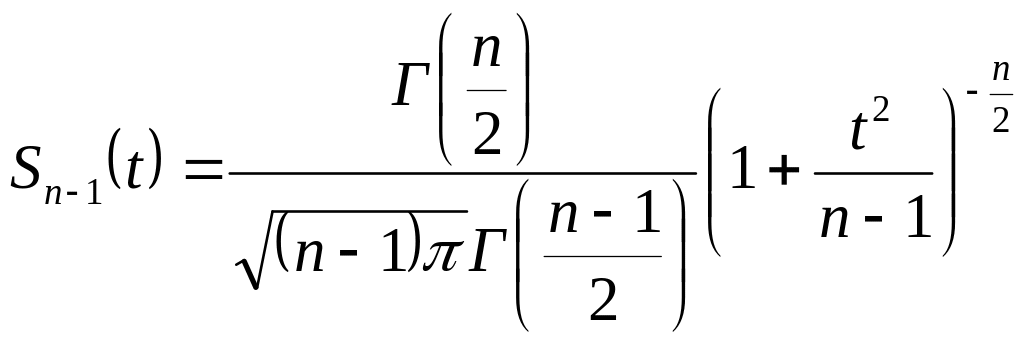 ,
,
где
Г![]() - гамма –функция:
- гамма –функция:
![]() .
.
Доверительный интервал для дисперсии, покрывающий точку D с вероятностью , находится
 ,
,
где
![]() и
и
![]() - критические точки
- критические точки![]() («хи-квадрат») распределения с n-1
степенями свободы и соответствующими
(«хи-квадрат») распределения с n-1
степенями свободы и соответствующими
![]() и
и
![]() уровнями значимости,
уровнями значимости,
![]() ,
n
– объем
выборки. Критические точки находят по
таблице критических точек распределения
«хи-квадрат»
(табл. 3 приложения).
,
n
– объем
выборки. Критические точки находят по
таблице критических точек распределения
«хи-квадрат»
(табл. 3 приложения).
Можно также по
выборке
![]() построить доверительный интервал для
следующего (n+1)-го,
наблюдения (то есть определить границы,
в которых оно будет лежать с заданной
вероятностью), а именно имеем
построить доверительный интервал для
следующего (n+1)-го,
наблюдения (то есть определить границы,
в которых оно будет лежать с заданной
вероятностью), а именно имеем
![]() .
.
Понятно, что это может быть полезно в качестве прогноза на будущее.
Пример. Из генеральной совокупности извлечена выборка объема n = 12:
Таблица 8
Варианта |
-0,5 |
-0,4 |
-0,2 |
0 |
0,2 |
0,6 |
0,8 |
1 |
1,2 |
1,5 |
Частота |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупности с помощью доверительного интервала.
Решение.
Найдем выборочное среднее
и исправленное выборочное среднее
квадратическое отклонение
.
Пусть условные варианты
![]() ,
тогда
,
тогда
![]() ;
;
![]() ;
;
 .
.
Для уровня значимости
![]() и числа степеней свободы
и числа степеней свободы
![]() по таблице распределения Стьюдента
находим критическую точку
=2,2
и определяем границы доверительного
интервала:
по таблице распределения Стьюдента
находим критическую точку
=2,2
и определяем границы доверительного
интервала:
![]() ;
;
![]() .
.
Таким образом, искомый доверительный интервал:
![]()
Пример.
Для отрасли,
включающей 1200 фирм, составлена случайная
выборка из 19 фирм. По выборке оказалось,
что исправленное среднее квадратическое
отклонение для числа работающих на
фирме составляет
![]() =25
(человек). пользуясь 90% -ым доверительным
интервалом, оценить среднее квадратическое
отклонение для числа работающих на
фирме по всей отрасли, построив
доверительный интервал.
=25
(человек). пользуясь 90% -ым доверительным
интервалом, оценить среднее квадратическое
отклонение для числа работающих на
фирме по всей отрасли, построив
доверительный интервал.
Решение. Доверительный интервал для параметра имеет вид
 ,
,
где
![]() и
и
![]() находят по таблице критических точек
распределения хи-квадрат. По таблице
определяем
= 28,9
находят по таблице критических точек
распределения хи-квадрат. По таблице
определяем
= 28,9
![]() ;
= 9,39
;
= 9,39
![]() .
Подставляя в формулу необходимые
величины, получаем искомый доверительный
интервал
.
Подставляя в формулу необходимые
величины, получаем искомый доверительный
интервал
![]() откуда
откуда
![]() (человек).
(человек).
Пример. За последние 5 лет годовой рост актива А составлял в среднем 20% со средним квадратическим отклонением (исправленным) 5%. Построить доверительный интервал с вероятностью 95% для цены актива в конце следующего года, если в начале года она равна 100 ден.ед.
Решение. Рассмотрим величины относительного прироста цены актива за год. Будем пользоваться нормальным приближением. Применяем формулу
![]() ,
,
где
![]() находим из таблицы распределения
Стьюдента:
находим из таблицы распределения
Стьюдента:
![]() .
.
Получаем
![]() ,
,
откуда
![]() .
.
Таким образом, цена актива в следующем году составит от 105 до 135 ден.ен.
