13.3. Вероятность попадания случайной точки в полуполосу

И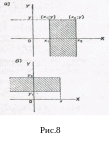 спользуя функцию распределения системы случайных величин X и Y , легко найти вероятность того, что в результате испытания случайная точка попадает в полуполосу и или в полуполосу и (рис. 8). Вычитая из вероятности попадания случайной точки в квадрант с вершиной вероятность попадания точки в квадрант с вершиной , получим

. Аналогично,

.

Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.

13.4. Вероятность попадания случайной точки в прямоугольник

Рассмотрим прямоугольник ABCD со сторонами, параллельными координатным осям (рис. 9). Пусть уравнения сторон таковы: . Найдем вероятность попадания случайной точки в этот прямоугольник. Искомую вероятность можно найти как разность вероятности попадания случайной точки в полуполосу АВ ( ) и вероятности попадания точки в полуполосу CD ( ) :

.

Рис. 9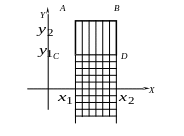

13.5. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности)

Двумерная случайная величина задавалась с помощью функции распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения.

Плотностью совместного распределения вероятностей двумерной непрерывной случайной величины называют вторую смешанную частную производную от функции распределения

.

Геометрически этой функции соответствует поверхность, которую называют поверхностью распределения.

Функцию можно рассматривать как предел отношения вероятности попадания случайной точки в прямоугольник (со сторонами и ) к площади этого прямоугольника, когда обе стороны прямоугольника стремятся к нулю.

Зная плотность совместного распределения , можно найти функцию распределения по формуле

,

что следует из определения плотности распределения двумерной непрерывной случайной величины .

Тогда вероятность попадания случайной точки в область D

.

Геометрически это равенство можно истолковать так: вероятность попадания точки в область D равна объему тела, ограниченного сверху поверхностью , основанием которого служит проекция этой поверхности на плоскость .

Свойства двумерной плотности вероятности

1. Двумерная плотность вероятности неотрицательна: .

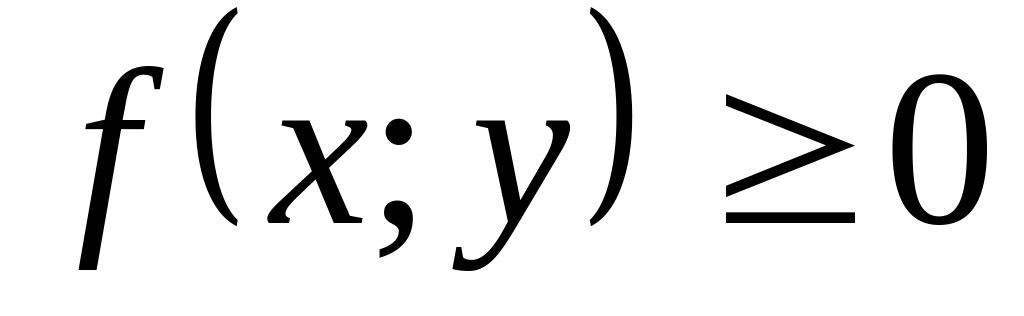2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:

.

Плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей

;

.

13.6. Условные законы распределения составляющих системы дискретных случайных величин

Пусть - непрерывная случайная величина.

Условной плотностью распределения составляющих X при данном значении Y=y называют отношение совместного распределения системы к плотности распределения составляющей Y:

/ .

Отличие условной плотности от безусловной состоит в том, что условная плотность дает распределение X при условии, что составляющая Y приняла значение Y=y; функция дает распределение X независимо от того, какие из возможных значений приняла составляющая Y.

Аналогично, для условной плотности составляющей Y при данном значении X=x.

Отсюда: закон распределения системы случайных величин

= или = .

Условные плотности распределения обладают свойствами:

, ;

, .